как узнать площадь куба
Площадь поверхности куба
Онлайн калькулятор

Теория
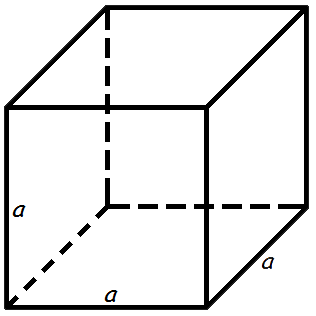
Площадь поверхности куба через ребро
Чему равна площадь поверхности куба Sпов, если длина его ребра a:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :
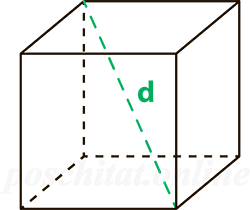
Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:
Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²
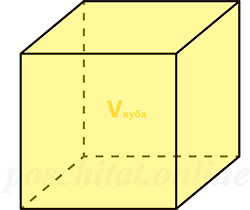
Площадь поверхности куба через объем
Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:
Sпов = 6 ⋅ 3 √ 8² = 6 ⋅ 3 √ 64 = 6 ⋅ 4 = 24 см²
Площадь поверхности куба.
Площадь поверхности куба – это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Определение площади поверхности куба.
Чему равна площадь поверхности куба.
Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба.
площадь куба
Площадь куба, формула площади куба, найти площадь куба онлайн.
Площадь куба, формула, площадь куба онлайн.
Формула площади куба
Формула площади куба звучит так :
Площадь куба равна 6 умноженное на а²
Доказательство формулы куба :
И каждая сторона состоит из квадрата, со стороной «а».
А раз сторон 6, то нужно площадь одного квадрата умножить на 6.
Формула площади сечения куба
То формула площади сечения куба звучит так:
Сечение площади куба равно произведению квадрата стороны на корень из двух.
Доказательство формулы сечения куба
Если мы переведем в наши буквенные обозначения, для нашего треугольника, то:
В нашем случае AB = AC= a из чего получаем :
Теперь извлекаем корень с двух сторон:
Мы нашли одну сторону сечения куба:
Теперь мы по\можем построить сечение куба:
Т.е нам нужно найти площадь прямоугольника BCDE.
Площадь прямоугольника равна :
Выше, мы BC уже нашли BC = а √ 2
Как мы знаем из условия, что это куб, а у куба все стороны равны, то CD = «a».
Задача : найдите площадь куба, если известна сторона.
Найдите площадь куба. если известна сторона куба, которая равна 5см.
Вспоминаем уже приведенную формулу куба :
S = 6a² = 6 * 5² = 6 * 25 = 150 Ответ:
Если сторона куба равна 5см, то площадь куба равна 150см²
Задача : найдите площадь сечения куба.
Найдите площадь сечения куба, если известна сторона, которая равна 10см.
Для решения данной задачи, нам потребуется знать формулу сечения площади куба
Заменяем а на 10, корень квадратный из 2 округлим до 1.4 :
S = 10² √ 2 = 100 * 1.4 = 140см².
Найти площадь куба онлайн
Для того чтобы найти площадь куба онлайн, вам требуется в поле :
Площадь куба
Свойства
Площадь куба, она же площадь полной поверхности куба, равна увеличенной в шесть раз площади одной его грани. Так как площадь куба зависит только от ребра, зная ее, можно легко вычислить ребро и затем все остальные параметры куба. S_(п.п.)=6a^2 a=√(S_(п.п.)/6)
Для того чтобы найти объем куба, необходимо его ребро возвести в третью степень. Используя полученную формулу ребра куба через площадь полной поверхности, получим, что объем куба равен одной шестой квадратного корня из площади куба в третьей степени, деленной на шесть. V=a^3=(√(S_(п.п.)/6))^3=1/6 √(〖S_(п.п.)〗^3/6)
Периметр куба можно найти, умножив ребро куба на 12. Если подставить вместо ребра квадратный корень через площадь куба, то получим следующую формулу для периметра куба: P=12a=12√(S_(п.п.)/6)
Диагональ одной стороны куба является по определению диагональю квадрата, которая вычисляется как произведение стороны квадрата на корень из двух. Так как ребро куба является стороной этого квадрата, то диагональ будет равна квадратному корню из площади, деленной на 3. d=a√2=√(S_(п.п.)/3)
Чтобы рассчитать диагональ куба, необходимо провести дополнительное построение на чертеже, соединяющее ребро куба и одну из вершин диагонали в прямоугольный треугольник. Это дает возможность воспользоваться теоремой Пифагора и вычислить диагональ куба через площадь, подставив формулу вместо ребра куба. (рис.2.1) a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3=√(S_(п.п.)/2)
Радиус сферы, вписанной в куб, по определению равен половине ребра куба или половине квадратного корня из площади куба, деленной на шесть. (рис. 2.2) r=a/2=1/2 √(S_(п.п.)/6)
Радиус сферы, описанной вокруг куба, представлен половиной диагонали куба, которая равна площади полной поверхности куба, деленной на два, под корнем. (рис.2.3) R=D/2=1/2 √(S_(п.п.)/6)
Формулы площади поверхности геометрических фигур
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба:
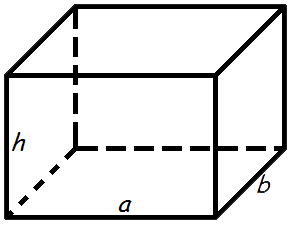
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра:
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра:
Площадь конуса
Формула площади боковой поверхности конуса:
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
Площадь шара
Формулы площади шара:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.