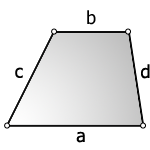
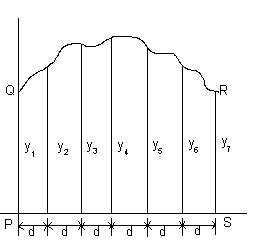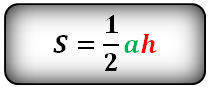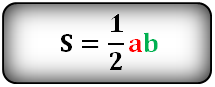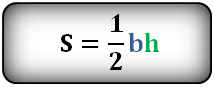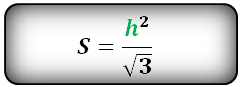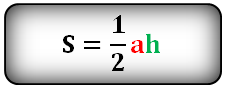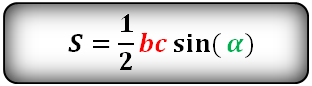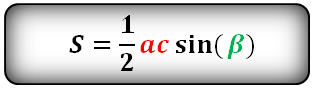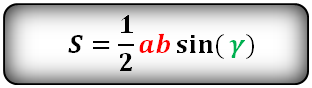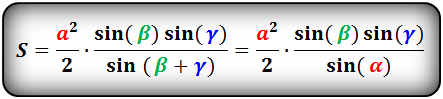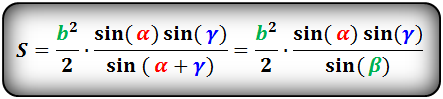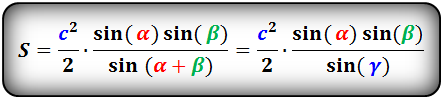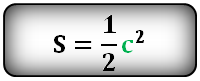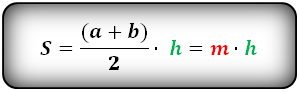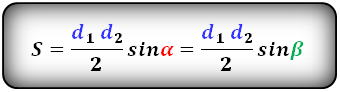как узнать площадь неправильной фигуры
Площадь неправильного четырехугольника
Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
Площади неправильных фигур.
Площади неправильных фигур.
Формула трапеций.
Правило средних ординат.
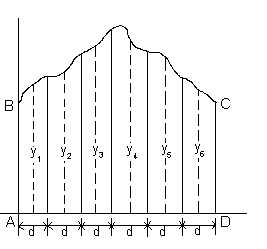
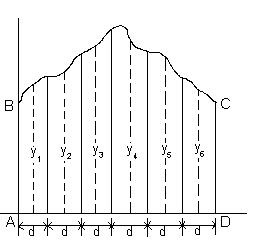
Чтобы определить площадь ABCD на рис. выше, необходимо:
Формула Симпсона
Чтобы определить площадь PQRS на рис.выше, необходимо:
Пример. Определение площади под кривой с помощью формулы трапеций, правила средних ординат, формулы Симпсона.
Машина стартует из состояния покоя, и ее скорость измеряется каждую секунду в течение 6 секунд:
| Время t [c] | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость v [м/c] | 0 | 3,0 | 6,0 | 9,15 | 13,5 | 18,5 | 25,0 |
Хотя мы понимаем что увеличение числа разбиений увеличивает точность, но для простоты решения возьмем количество разбиений, равное 7.
Определить расстояние, пройденное за 6 секунд (т.е. площадь под графиком):
а) по формуле трапеций, б) по правилу средних ординат, в)по формуле Симпсона.
а) Формула трапеций.
б) Правило средних ординат.
Площадь многоугольника
Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники
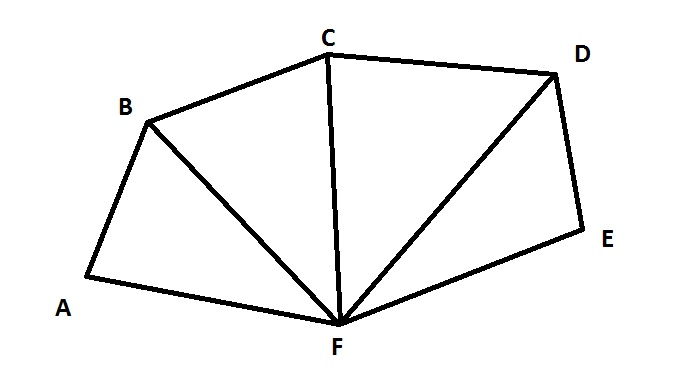
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площади неправильных фигур.
Площади неправильных фигур.
Площади неправильных плоских фигур можно приблизительно определить, используя планиметр, формулу трапеций, правило средних ординат, формулу Симпсона.
Подобные методы могут быть использованы, например, инженерами для оценки площадей индикаторных диаграмм паровых двигателей, землемерами для оценки площадей земельных участков, кораблестроителями для оценки горизонтальных или поперечных сечений кораблей.
Планиметр.
Это инструмент для непосредственного измерения малых площадей, очерченных неправильной кривой.
Формула трапеций.
— Разделить PS на любое число равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность).
— Аккуратно измерить ординаты у1, у2, у3 и так далее.
В общем, согласно формуле трапеций: Площадь = (ширина интервала)[1/2(первая + последняя ордината)+(сумма остальных ординат)].
Правило средних ординат.
Чтобы определить площадь ABCD на рис. выше, необходимо:
— Разделить основание AD на любое количество равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность).
— Восстановить перпендикуляр из середины каждого интервала (на рис. выше оказаны штриховыми линиями).
-Точно измерить ординаты у1, у2, у3 и так далее.
В общем виде, правило средних ординат гласит: Площадь = (ширина интервала)*(сумма средних ординат).
Чтобы определить площадь PQRS на рис.выше, необходимо:
— Разделить основание PS на четное количество равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность).
— Точно измерить ординаты у1, у2, у3 и так далее.
В общем виде, формула Симпсона: Площадь = 1/3(ширина интервала)[(первая + последняя ордината)+4(сумма четных ординат)+2(сумма нечетных ординат)].
Пример. Определение площади под кривой с помощью формулы трапеций, правила средних ординат, формулы Симпсона.
Машина стартует из состояния покоя, и ее скорость измеряется каждую секунду в течение 6 секунд:
| Время t [c] | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость v [м/c] | 0 | 3,0 | 6,0 | 9,15 | 13,5 | 18,5 | 25,0 |
Хотя мы понимаем что увеличение числа разбиений увеличивает точность, но для простоты решения возьмем количество разбиений, равное 7.
Определить расстояние, пройденное за 6 секунд (т.е. площадь под графиком):
а) по формуле трапеций, б) по правилу средних ординат, в)по формуле Симпсона.
а) Формула трапеций.
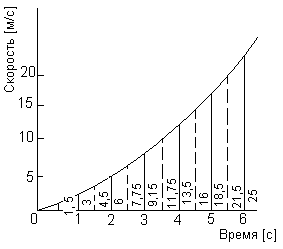
Время на графике делится на 6 интервалов шириной 1 с и измеряются ординаты. Итак, площадь S определяется формулой
S= 1[(0+25)/2 +3+6+ 9,15+13,5+18,5]=62,65 м
б) Правило средних ординат.
Время на графике делится на 6 интервалов шириной 1 с. На рис. пунктирной линией показаны средние ординаты. Измерена каждая средняя ордината. Итак, площадь S определяется формулой
S= 1(1,5 +4,5+7,75+11,75+16+21,5)=63 м
Время на графике делится на 6 интервалов шириной 1 с и измеряются ординаты. Итак, площадь S определяется формулой:
S= (1/3)*[(0+25) +4(3+9,15+ 18,5)+2(6+13,5)]= 61,2 м.
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
Формула площади круга, (S):
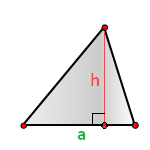
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
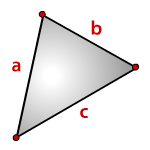
3. Площадь треугольника, формула Герона
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
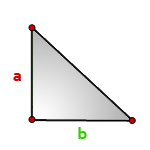
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
Формула площади прямоугольного треугольника, (S):
a — равные стороны

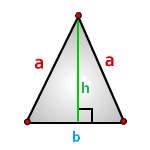
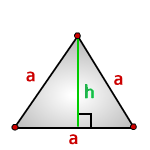
6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
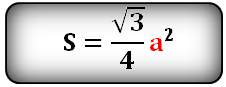
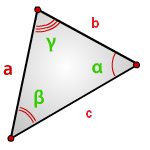
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
12. Площадь произвольной трапеции
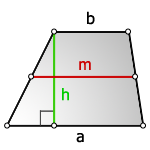
1. Формула площади трапеции через основания и высоту
Формула площади трапеции, (S):
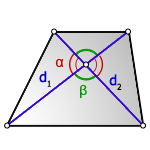
2. Формула площади трапеции через диагонали и угол между ними
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
Формула площади равнобедренной трапеции через основания и высоту, (S):