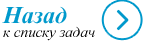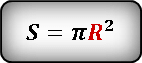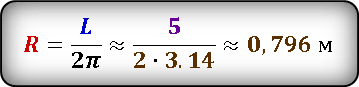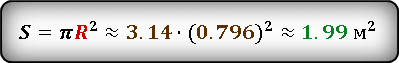как узнать площадь окружности зная длину окружности
Задача: определить площадь круга, если известна длина окружности
Условие задачи:
Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.
Дано:
Длина окружности, L = 5 м
Найти площадь круга: S
Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.
Определить радиус, нам поможет формула длины окружности.
После преобразования, выразим радиус через длину окружности и подставим значения.
Получили значение радиуса окружности.
В формулу площади круга, подставляем найденное значение радиуса.
Ответ:
Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение
Площадь круга
Площадь круга — это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве — определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.
Формулы площади круга
Площадь круга через радиус
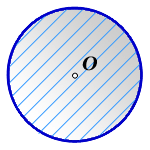
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь 
— площадь круга, 
— радиус круга.
В формуле фигурирует 
— это постоянная величина, которая называется «число » — это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно «число » равно 3,14. Хотя после цифры «4» еще бесконечное количество цифр:
Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр — это два радиуса, то, следовательно, радиус — это половина диаметра:
— диаметр круга.
Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность — это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: 
, тогда определим радиус и подставим его в формулу (1):
,
И формула площади круга через длину окружности:
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус 
см.
Решение: Для определения площади круга используем формулу (1):
Задача 2
Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
Задача 3
Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.
Решение: граница участка круглой формы — это окружность. Тогда длина этой границы — это длина окружности. Площадь участка — площадь круга, которую мы определим по формуле (3) через длину окружности:
Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.
Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
или длину окружности 
.
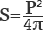
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Площадь круга
Существует несколько формул для нахождения площади круга. На нашем сайте мы предлагаем вам расчет по трем формулам. В зависимости от исходных данных, площадь круга можно найти через:
Круг — множество точек плоскости, удаленных от заданной точки этой плоскости (эту точку называют центр круга) на расстояние, не превышающее заданное (это расстояние — радиус круга).
Площадь круга онлайн калькулятор
Площадь круга через радиус
Чтобы найти площадь круга, зная его радиус, необходимо воспользоваться формулой:
S= \pi r^2
В этой формуле r — радиус круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через диаметр
Диаметр — отрезок, проходящий через центр окружности и соединяющий две точки на окружности. Диаметр равен двум радиусам.
Если известен диаметр круга, то его площадь можно найти по формуле:
S= \dfrac<\pi><4>d^2
Здесь d — диаметр круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через длину окружности
Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг.
В случае, когда известна длина окружности, площадь круга можно рассчитать по следующей формуле:
S= \dfrac
Здесь l — длина окружности, а \pi — число Пи, которое приблизительно равно 3,14.
Способы вычисления площади круга
Основные способы вычисления площади круга, формулы
Перед тем, как рассмотреть методы нахождения площади круга, введем основные понятия.
Круг — это участок плоскости, который расположен внутри окружности.
Окружность — это замкнутая плоская кривая, включающая множество точек, находящихся на одинаковом расстоянии от центра.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Радиус представляет собой отрезок, ограниченный с одной стороны центром круга, с другой — любой точкой, находящейся на внешней окружности данной фигуры.
Диаметром называется такой отрезок, который проходит через центр окружности и соединяет две точки рассматриваемой кривой.
Теперь разберем основные способы нахождения площади круглой фигуры.
Через радиус
Данный метод предполагает, что нам известен радиус круга, площадь которого нужно найти. Вычисления выполняются по формуле, согласно которой площадь круга равна квадрату радиуса, умноженному на число Пи. В записи указанная формула имеет вид:
Через диаметр
Если мы располагаем информацией о диаметре, то для расчета площади круга можно применить выражение, по которому искомая величина будет равна квадрату диаметра, умноженного на частное числа Пи и 4. То есть формула выглядит так:
Через длину окружности
Для того, чтобы воспользоваться этим способом, необходимо знание длины окружности (L). В этом случае площадь круга представлена как частное, в котором делитель равен квадрату длины окружности, а делитель — это произведение числа Пи и 4. На математическом языке данная формула записывается так:
Площадь круга описанного вокруг квадрата
Бывают ситуации, когда внутри круга расположен квадрат, а все его четыре вершины принадлежат окружности заданного круга. Чтобы найти площадь круга, достаточно знать сторону правильного четырехугольника, который он описывает. Тогда площадь поверхности заданной фигуры равняется произведению числа Пи и половины квадрата этой стороны, то есть:
Нахождение через площадь сектора круга
Сектор круга представляет собой участок круговой плоскости, которая ограничена с двух сторон радиусами, а с третьей стороны — дугой.
Существует два метода расчета площади кругового сектора:
Примеры задач с решением
Найдите площадь круга, если известно, что длина окружности составляет 85 миллиметров.
Произведем расчеты на основании известной формулы:
Детская песочница имеет квадратную форму со стороной, равной 1,5 метрам. По технологии песочницу устанавливают на прорезиненном участке круглой формы, равном кругу, в который можно вписать такую песочницу. Найдите площадь территории, на которую нужно уложить резиновую крошку.
Воспользуемся формулой: \(S=0,5a^2\mathrm\pi=0,5\cdot1,5^2\cdot13,14=14,7825 \)