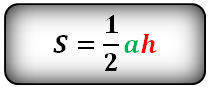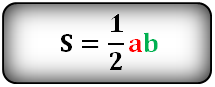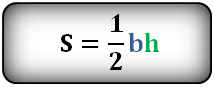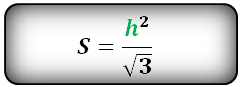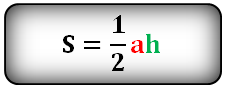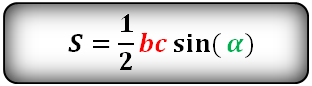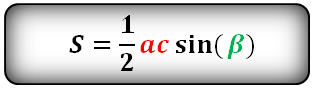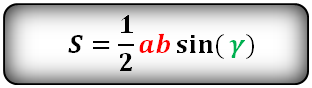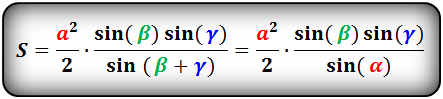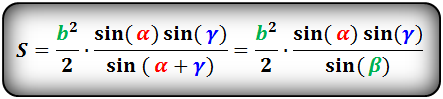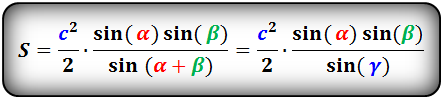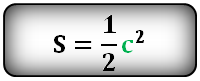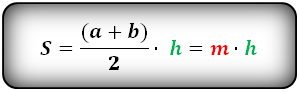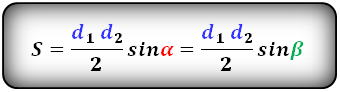как узнать площадь овала
Вычисление площади эллипса онлайн
Наш онлайн калькулятор вычисляет площадь эллипса через его полуоси, a и b. Для того чтобы найти площадь эллипса введите значения полуосей и нажмите кнопку «Вычислить», калькулятор выдаст ответ и пошаговое решение!

Как найти площадь эллипса
На этом сайте при помощи онлайн калькулятора можно посчитать площадь эллипса по его двум полуосям. На рисунке они отмечены латинскими буквами a и b. Для расчёта достаточно знать эти две величины и значение числа ПИ, которое остается всегда постоянной единицей и равняется 3.14.
Формула для определения площади эллипса выглядит следующим образом:
где S – площадь, ПИ = 3.14, a и b – длина полуосей.
Введите известные значения полуосей в специальные строчки и нажмите «Вычислить». Сразу после этого на экране появится решение и результат, что поможет вам для дальнейших математических и геометрических действий, а так же для работы и учебы.
Онлайн калькулятор хорошо использовать в качестве подручной вычислительной техники в сложных ситуациях и при решении математических задач, что пригодится будущим и настоящим студентам, а так же школьникам и преподавателям.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
Онлайн калькулятор площади эллипса. как узнать площадь эллипса
Формула для вычисления площади фигуры, ограниченной параметрически заданной линией.
Эта формула получается из формулы площади криволинейной трапеции подстановкой :
Если функция не является основной элементарной, то для выяснения ее возрастания или убывания может потребоваться теория из раздела возрастание и убывание функции на интервале.
Решаем задачи вместе
Пример 2. Найти объём шара радиуса R.
Пример 3. Найти объём тела, образованного вращением вокруг оси
абсцисс () фигуры, заключённой между параболами
и
.
и —
абсциссам точек B и D пересечения парабол. Теперь можем найти объём тела:
Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга (). Форму тора имеет, например, баранка).
Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.
Уравнение окружности LBCD имеет вид
причём уравнение кривой BCD
а уравнение кривой BLD
Используя разность объёмов тел, получаем для объёма тора v выражение
Пример 5. Найти объём тела, образованного вращением вокруг оси
ординат () фигуры, ограниченной линиями
и
.
и —
ординаты точек O и B пересечения параболы и прямой. Таким образом, получаем объём тела:
Примеры вычисления площади фигуры, ограниченной параметрически заданной кривой.
Рассмотрим примеры применения полученной формулы, позволяющей вычислять площади фигур, ограниченных параметрически заданными линиями.
В нашем примере параметрически заданная линия представляет собой эллипс с полуосями 2 и 3 единицы. Построим его.
Что мы имеем:
Тогда площадь половины эллипса находится как
А вот правую или левую половины эллипса взять не получится.
Решим еще один пример.
Забегая немного вперед, кривая является «вытянутой» астроидой. (Астроида имеет следующее параметрическое представление ).
Остановимся подробно на построении кривой, ограничивающей фигуру. Строить ее мы будем по точкам. Обычно такого построения достаточно для решения большинства задач. В более сложных случаях, несомненно, потребуется детальное исследование параметрически заданной функции с помощью дифференциального исчисления.
Для удобства занесем значения в таблицу:
Отмечаем точки на плоскости и ПОСЛЕДОВАТЕЛЬНО соединяем их линией.
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
Формула площади круга, (S):
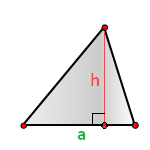
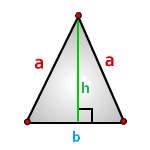
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
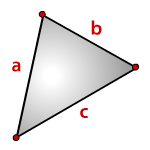
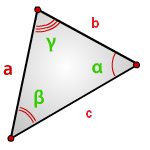
3. Площадь треугольника, формула Герона
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
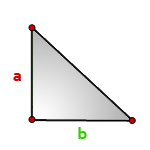
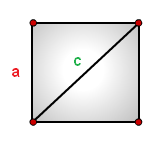
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
Формула площади прямоугольного треугольника, (S):
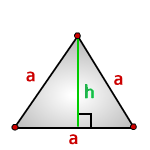
a — равные стороны

6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
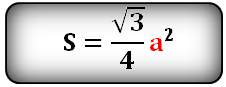
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
Площадь треугольника через сторону и два угла (S):
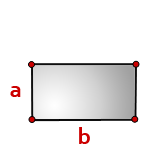
9. Формула расчета площади прямоугольника
Формула площади прямоугольника, (S):
10. Как рассчитать площадь квадрата через диагональ или сторону
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
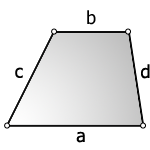
12. Площадь произвольной трапеции
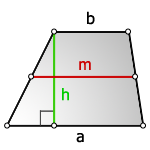
1. Формула площади трапеции через основания и высоту
Формула площади трапеции, (S):
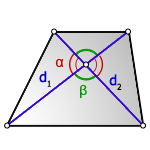
2. Формула площади трапеции через диагонали и угол между ними
Формула площади трапеции, (S):
3. Формула площади трапеции через четыре стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
Формула площади равнобедренной трапеции через основания и высоту, (S):