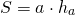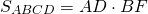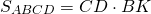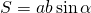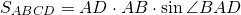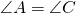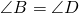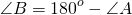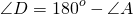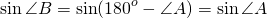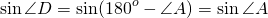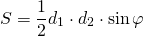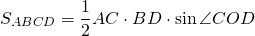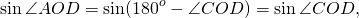как узнать площадь параллелограмма
Площади фигур. Площадь параллелограмма.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей
одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь
будет равна числу этих квадратов.
Параллелограмм это четырехугольник, у которого противоположные стороны попарно параллельны и
лежат на параллельных прямых.
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус
Воспользуйтесь нашим калькулятором для расчета площади параллелограмма.
Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.
Формулы для определения площади параллелограмма:
1. Площадь параллелограмма по длине стороны и высоте.
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону
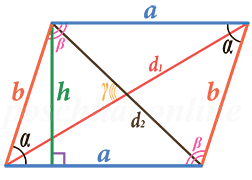
2. Площадь параллелограмма по двум сторонам и углу между ними.
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
3. Площадь параллелограмма по двум диагоналям и углу между ними.
d1, d2 — длины диагоналей параллелограмма,
Площадь параллелограмма
Для начала, чтобы узнать и найти площадь
параллелограмма. Дадим определения
некоторым важным понятиям, связанными так
или иначе с параллелограммом. Это понятие
высоты в параллелограмме и его основания.
Основание параллелограмма — это прямая, на которую
можно опустить перпендикуляр из любой точки
с противоположной стороны параллелограмма.
Высота в параллелограмме — это отрезок, являющийся
перпендикуляром, который связывает два основания.
Грубо говоря, если с какой-то из сторон параллелограмма
можно опустить перпендикуляр на противоположную сторону, то
сторона на которую упадет перпендикуляр будет являться
основанием, а сам перпендикуляр — высотой.
Чтобы выразить площадь параллелограмма, нужно
внимательно рассмотреть его. Рассматривая
произвольный параллелограмм, можно заметить,
что он состоит из двух прямоугольных треугольников
и одного прямоугольника. Так, что можно смело заявить:
площадь параллелограмма — это площадь
прямоугольника + площадь двух треугольников.
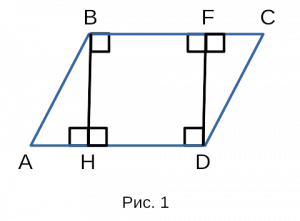
На рисунке 1 изображен параллелограмм ABCD. Площадь S
параллелограмма ABCD, с высотами BH и DF,
равна BF*BH + ½BH*AH + ½FC*FD. Но это очень громоздкая
формула. Математики сократили её и получили современную
формулу площади параллелограмма через высоту и основание.
Площадь S параллелограмма ABCD, с основанием AD
и высотой BH равна AD*BH.
Площадь параллелограмма — это площадь фигур,
на которые можно разбить параллелограмм.
Площадь параллелограмма численно равна
произведению его основания на высоту.
Теперь, если вы поняли как методом рассмотрения геометрической фигуры,
мы получили площадь параллелограмма, вы сможете найти площадь
большинства других геометрических фигур!
Как найти площадь параллелограмма
Онлайн калькулятор
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
Зная длины сторон a и b, и угол α
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см 2
Зная длины сторон a и b, и угол β
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см 2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
S = 2 √ 12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅ √ 12⋅4⋅7⋅1 = 2⋅ √ 336 = 36.66 см 2
Зная длины диагоналей d1 и d2, и угол между ними γ
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см 2
Нахождение площади параллелограмма: формула и примеры
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.
Формула вычисления площади
По длине стороны и высоте
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По двум сторонам и углу между ними
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a ⋅ b ⋅ sin α
По двум диагоналям и углу между ними
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
Примеры задач
Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.
Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.
Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.
Площадь параллелограмма
Площадь параллелограмма можно найти по стороне и проведённой к этой стороне высоте, по двум сторонам и углу, по диагоналям и углу между ними.
I. Площадь параллелограмма по стороне и высоте
Площадь параллелограмма равна произведению стороны параллелограмма на высоту, проведённую к этой стороне.
Формула для нахождения площади параллелограмма через сторону и высоту:

II. Площадь параллелограмма по сторонам и углу
Площадь параллелограмма равна произведению его сторон на синус угла между ними.
Формула для нахождения площади параллелограмма через стороны и угол:
Например, площадь параллелограмма ABCD
По свойствам параллелограмма, противоположные углы параллелограмма равны:
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, то есть,
А так как синус тупого угла равен синусу смежного ему угла, то
Таким образом, площадь параллелограмма можно найти как произведение его двух любых не смежных сторон на синус любого угла.
III. Площадь параллелограмма по диагоналям
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
Формула площади параллелограмма через диагонали:

то в качестве угла между диагоналями можно брать любой угол — как острый, так и тупой (прямой — в ромбе и квадрате).