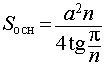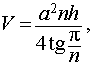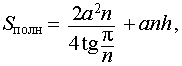как узнать площадь призмы
Площадь призмы
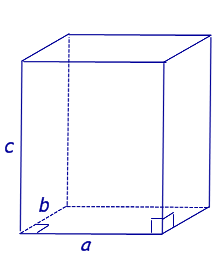
Призма – это многогранник, в основаниях которого два равных многоугольника, а боковые грани представляют собой параллелограммы.
Площадь боковой поверхности призмы также как и прямоугольного параллелепипеда состоит из прямоугольников, если призма прямая, сторонами которых являются сторона многоугольника в основании и высота, а их количество зависит от количества сторон в многоугольнике. Поэтому площадь боковой поверхности призмы вычисляется умножением периметра основания на высоту: Sб.п.=Ph=nah
Если в основании призмы лежит правильный треугольник, то в формуле соответственно вместо n мы напишем 3 : Sб.п.=3ah
Если в основании призмы лежит правильный четырехугольник, то есть квадрат, то формула будет выглядеть так: Sб.п.=4ah
Формула для прямоугольника: Sб.п.=2(a+b)h
Формула для пятиугольника: Sб.п.=5ah
Формула для шестиугольника: Sб.п.=6ah
Чтобы найти площадь полной поверхности, нужно традиционно добавить к площади боковой два основания:
Для правильного треугольника в основании:
Для прямоугольника в основании: Sп.п.=2ab+2bc+2ac
Для пятиугольника в основании:
Для шестиугольника в основании:
Призма
Призма
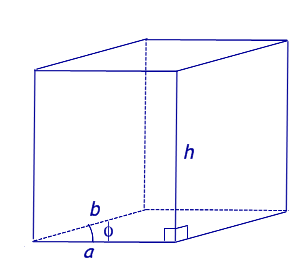
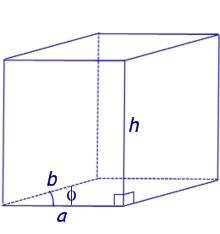
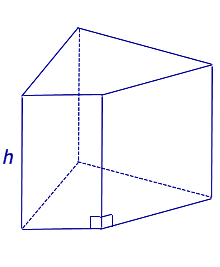
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
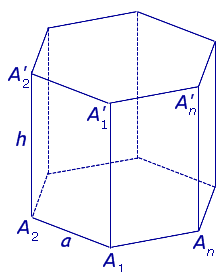
Чтобы были понятны формулы, введем обозначения:
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
В основании лежит четырехугольник
1. Прямоугольник
2. Ромб
3. Трапеция
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Средняя линия треугольника параллельна основанию и равна его половине.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Нахождение площади правильной призмы: формула и задачи
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание | » data-order=» «> «>  |
| боковая поверхность | |
| полная | » data-order=» «> «>  |
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | |
| боковая поверхность | |
| полная |
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a 2 . А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a 2 .
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание | » data-order=» «> «>  |
| боковая поверхность | |
| полная | » data-order=» «> «>  |
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
Калькулятор площади поверхности призмы
Призма — это многогранник, в основании которого располагается многоугольник, а боковые грани представляют собой параллелограммы. Призматические фигуры встречаются в нашей жизни на каждом шагу, поэтому важно уметь знать основные свойства призм.
Что такое призма
Призма представляет собой две конгруэнтные n-угольные грани, лежащие в параллельных плоскостях и n-количество граней-параллелограммов, которые расположены на сторонах n-угольника. Простыми словами, если в основании призмы лежит квадрат, то фигура превращается в куб. Если пентагон, то в пятиугольную призму, если гексагон — в шестиугольную. Если же количество сторон многоугольника, лежащего в основании, стремится к бесконечности, то фундамент призмы превращается в круг, а сама фигура трансформируется в цилиндр. Таким образом, призма — это частный случай некругового цилиндра.
Призмы имеют большое распространение в реальной жизни. В отличие от конусов или тетраэдров, призматическую форму имеет огромное количество предметов, вещей или деталей. К примеру, кирпич — это призма, кирпичное помещение с параллельными стенами — тоже призма, любое здание, состоящее из этих помещений — призматическая фигура. И даже мебель в этих зданиях имеет геометрию призмы. Наш мир состоит из разных призм, поэтому формула определения поверхности фигуры может вам понадобиться во многих жизненных ситуациях.
Площадь поверхности призмы
Площадь правильной призматической фигуры — это сумма всех площадей боковых поверхностей, а также нижнего и верхнего оснований. Площадь боковой поверхности находится как сумма площадей параллелограммов:
где n — количество граней, a — сторона параллелограмма, а h — его высота.
Площадь оснований вычисляется по формулам расчета площадей соответствующих многоугольников. К примеру, если в основании призмы лежит равносторонний треугольник, то
а если правильный шестиугольник, то
Так как призма имеет два одинаковых основания, то формула общей площади поверхности фигуры принимает вид:
Если вам необходимо найти площадь поверхности правильной призматической фигуры, то воспользуйтесь нашим онлайн-калькулятором. Для вычисления вам понадобится ввести три переменных:
Рассмотрим примеры использования данной формулы в реальной жизни.
Примеры
Допустим, вы решили обить вагонкой беседку, которая геометрически представляет собой шестиугольную призму. Вам необходимо узнать, сколько квадратных метров вагонки понадобится для обустройства уютной беседки. Вы не собираетесь обшивать пол и потолок, поэтому вам необходимо узнать только площадь боковой поверхности домика. Для этого введите в форму онлайн-калькулятора высоту беседки h = 2,5 м, длину одной стороны домика a = 3 м и количество граней призмы, равное n = 6. Вы получите результат в виде:
S = 2 × 23,38 + 45 = 91,76,
то есть площадь потолка и пола равны по 23,3 квадратных метра, а боковая поверхность составляет 45 квадратных метров. Таким образом, для обшивки стен беседки вам понадобится 45 квадратов вагонки.
Работа
Представим, вы работаете на прокатном стане и отвечаете за обработку металлопроката защитным составом. Для определения компонентов и необходимого количества состава вы должны знать общую площадь поверхности обрабатываемой детали. Стальной квадрат — металлическое изделие, которое используется в производстве деталей машин и представляет собой длинную четырехугольную призму. Для определения площади металлоизделия введите в онлайн-калькулятор его параметры. Стандартный квадрат имеет длину h = 6 м и сторону основания a = 12 см= 0,12 м. Вы получите результат в виде:
S = 2 × 0,0144 + 2,8800 = 2,9088
Таким образом, площадь поверхности стальной детали составляет 2,908 квадратных метров, и теперь вы сможете правильно рассчитать компоненты для приготовления защитного покрытия.
Заключение
Огромное количество предметов в нашей жизни имеет форму призмы, поэтому расчет ее площади может понадобиться в самых неожиданных ситуациях. К примеру, вычисление площади призматических фигур необходимо при проектировании деталей машин или элементов произведений архитектуры. Расчет площади необходим инженерам-технологам на производстве или обычным гражданам в быту, например, при поклейке обоев или покраске деревянных брусьев лаком.
Формулы для объема, площади боковой поверхности
и площади полной поверхности призмы
Введем следующие обозначения:
| V | объем призмы |
| Sбок | площадь боковой поверхности призмы |
| Sполн | площадь полной поверхности призмы |
| Sосн | площадь основания призмы |
| Pосн | периметр основания призмы |
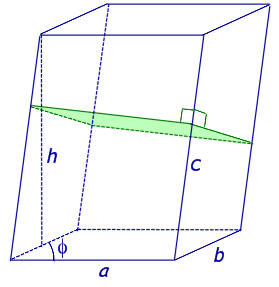
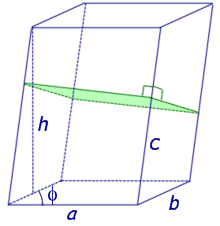
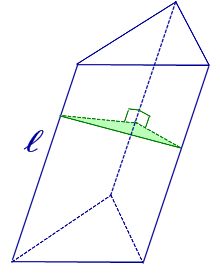
| Pперп | периметр перпендикулярного сечения призмы |
| Sперп | площадь перпендикулярного сечения призмы |
Используя эти обозначения, составим таблицу с формулами для вычисления объемов, площадей боковой поверхности и площадей полной поверхности различных видов призм.