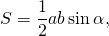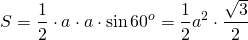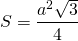как узнать площадь равностороннего треугольника

Как найти площадь равностороннего треугольника

Онлайн калькулятор

Чтобы вычислить площадь равностороннего треугольника вам нужно знать следующие параметры (либо-либо):

Введите их в соответствующие поля и узнаете площадь равностороннего треугольника (S).

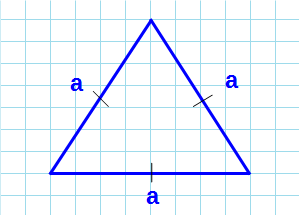
Как посчитать площадь равностороннего треугольника зная длину равных сторон

Какова площадь равностороннего треугольника (S) если известна длина сторон (a)?

Формула

Пример

Если сторона a = 2 см, то:

S = √3 /₄ ⋅ 2² = 1.732 /₄ ⋅ 4 ≈ 1.732 см 2

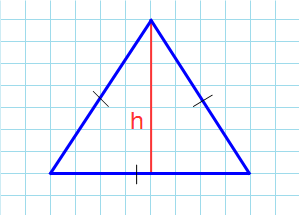
Как посчитать площадь равностороннего треугольника зная его высоту

Какова площадь равностороннего треугольника (S) если известна его высота (h)?

Формула

Пример

Если высота h = 3 см, то:

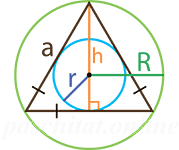
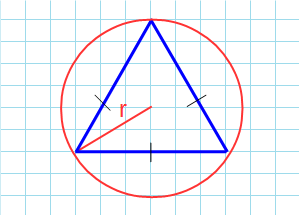
Как посчитать площадь равностороннего треугольника зная радиус описанной окружности

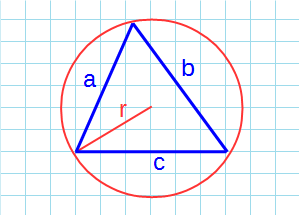
Какова площадь равностороннего треугольника (S) если известен радиус описанной окружности (R)?

Формула

Пример

Если радиус описанной окружности R = 4 см, то:

S = 3 ⋅ √3 /₄ ⋅ 4² = 3 ⋅ 1.732 /₄ ⋅ 16 = 1.299 ⋅ 16 ≈ 20.784 см 2

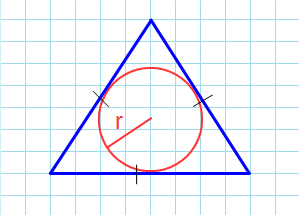
Как посчитать площадь равностороннего треугольника зная радиус вписанной окружности

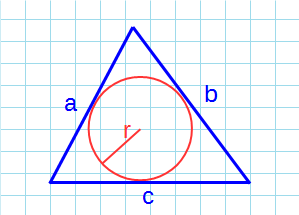
Какова площадь равностороннего треугольника (S) если известен радиус вписанной окружности (r)?

Формула

Пример

Если радиус вписанной окружности r = 1 см, то:

S = 3⋅ √ 3 ⋅ 1² = 3 ⋅ 1.732 ⋅ 1 ≈ 5.196 см 2

Как посчитать площадь равностороннего треугольника зная его периметр

Какова площадь равностороннего треугольника (S) если известен его периметр (P)?

Формула

Пример

Если периметр P = 8 см, то:

S = √3 /₃₆ ⋅ 8² = 1.732 /₃₆ ⋅ 64 ≈ 3 см 2

Источник

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

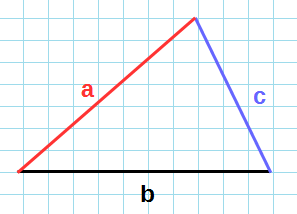
По формуле Герона

Формула Герона для нахождения площади треугольника:

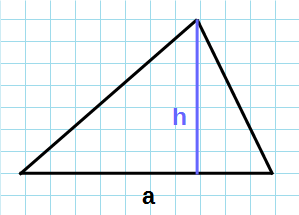
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

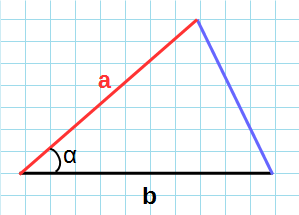
Через две стороны и угол

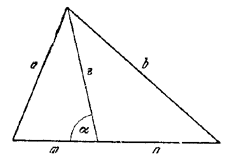
Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

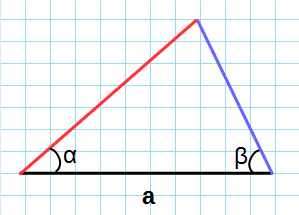
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

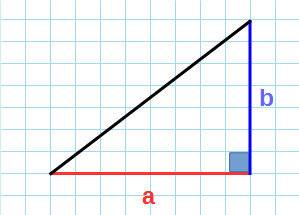
Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

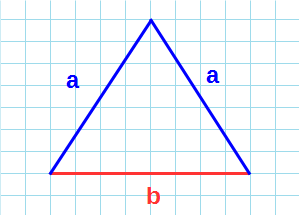
Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

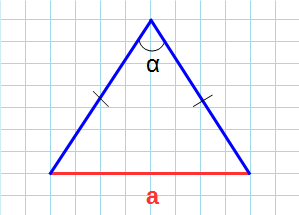
Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Источник

Площадь треугольника

Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.

Что такое треугольник

Треугольник — это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.

Сумма трех углов треугольника должна быть равна 180°.

Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).

Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.

Различные типы треугольников в зависимости от длины их сторон

Разносторонний треугольник

Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.

Равнобедренный треугольник

Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.

Прямоугольный треугольник

Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.

Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.

Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.

Равносторонний треугольник

Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.

Площадь треугольника

Площадь разностороннего треугольника

Вычисляем площадь треугольника без особенностей — все его стороны разные и все углы разные.

Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле «площадь треугольника через две стороны и угол между ними»:

Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:

Формула Герона определения площади треугольника

Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.

, где

Площадь равнобедренного треугольника

Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.

К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:

Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:

Площадь прямоугольного треугольника

Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:

Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе

Площадь прямоугольного треугольника, если в него вписана окружность:

Площадь равностороннего треугольника

Площадь равностороннего треугольника можно найти через радиус описанной окружности.

Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:

Площадь равностороннего треугольника, если известна высота треугольника:

Источник

Узнать ещё

Знание — сила. Познавательная информация

Площадь равностороннего треугольника

Площадь равностороннего треугольника может быть выведена с помощью одной из формул для вычисления площади треугольника. А с помощью этой ассоциации полученную формулу легко запомнить.

Сначала выведем формулу площади равностороннего треугольника.

Если воспользоваться формулой для нахождения площади произвольного треугольника,

Таким образом, площадь равностороннего треугольника вычисляется по формуле:

Теперь взгляните на числа, входящие в эту формулу: 2,3,4.

Они идут подряд один за другим. С помощью этой ассоциации формула площади правильного треугольника легко запоминается и воспроизводится даже в стрессовых условиях экзамена или контрольной.

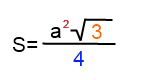
Можно еще отметить, что в площадь должна получаться в квадратных единицах. Поскольку из длин отрезков в формуле есть только а, то а — в квадрате, чтобы прийти к квадратным единицам.

Источник

Площадь равностороннего треугольника

Определение

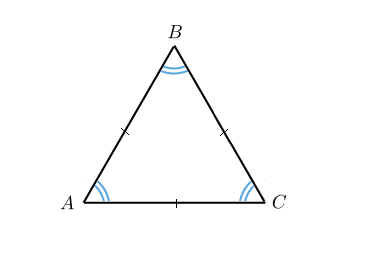
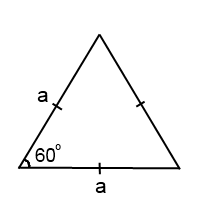
Правильным треугольником называют часть плоскости, ограниченную тремя одинаковыми отрезками. Их соединяют точки, которые не принадлежат одной прямой. Здесь все три угла одинаковые и равняются по 60 градусов. Поэтому для определения площади правильного треугольника можно будет пользоваться упрощенными формулами.

Равносторонний треугольник является частным случаем равнобедренного треугольника.

Значение площади правильного треугольника вычисляется путем подстановки параметров фигуры в классическую формулу.

Рис. 1. Правильный треугольник.

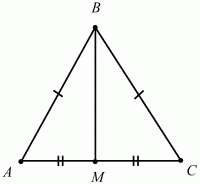
Нахождение площади правильного треугольника

В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.

Рис. 2. Рисунок к доказательству.

В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.

Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.

Тогда формула будет выглядеть следующим образом:

Теперь вспомним классическую формулу площади треугольника:

$S= <1\over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. Формула площади равностороннего треугольника будет выглядеть следующим образом:

ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.

Только в правильном треугольнике возможно нахождение площади через сторону.

По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.

Рис. 3. Произвольный треугольник.

Что мы узнали?

Площадь правильного треугольника можно вычислить через сторону, поскольку речь идет о фигуре с одинаковыми параметрами, или через высоту по классической формуле. Здесь углы также будут одинаковыми. При решении некоторых задач по геометрии стоит помнить о том, что высоты данной плоской фигуры, ограниченной тремя сторонами, равны между собой.

Источник