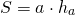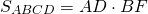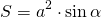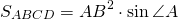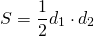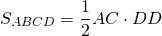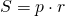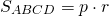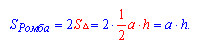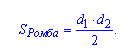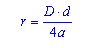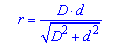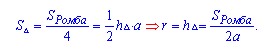как узнать площадь ромба
Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
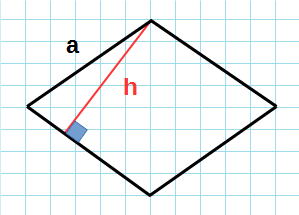
Через сторону и высоту
Формула для нахождения площади ромба через сторону и высоту:
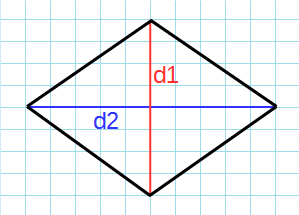
Через диагонали
Формула для нахождения площади ромба через диагонали:
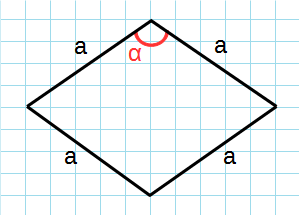
Через сторону и угол
Формула для нахождения площади ромба через сторону и угол:
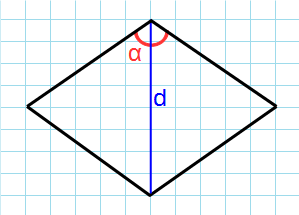
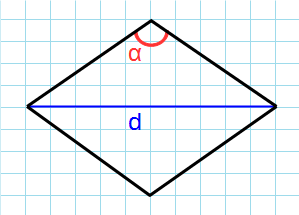
Через угол и диагональ из этого угла
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
Через угол и противолежащию диагональ
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
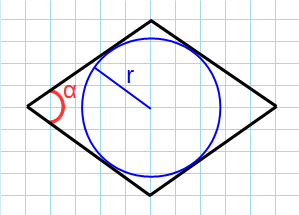
Через угол и радиус вписанной окружности
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Формула площади ромба через две диагонали:
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
a — сторона; sin α — синус угла;
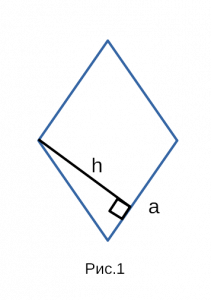
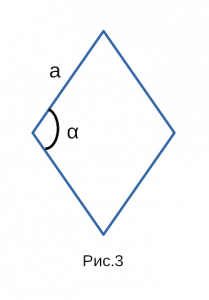
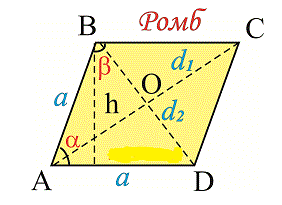
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
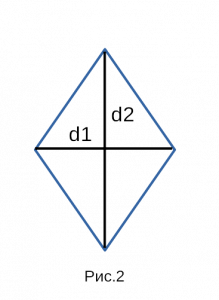
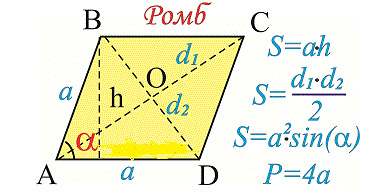
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Площадь ромба
Площадь ромба можно найти по формулам для нахождения площади параллелограмма. С учётом свойств ромба, некоторые из этих формул меняют свой вид.
I. Площадь ромба по стороне и высоте
Площадь ромба равна произведению стороны ромба и его высоты.
Формула для нахождения площади ромба по стороне и высоте не отличается от соответствующей формулы площади параллелограмма:

Так как все стороны ромба равны и все его высоты равны, для нахождения площади можно брать любую сторону и любую высоту.
II. Площадь ромба по стороне и углу
Площадь ромба равна произведению квадрата его стороны на синус угла.
Формула для нахождения площади ромба через сторону и угол:

Так как ∠D=180-∠A, sin∠D=sin(180-∠A)=sin∠A, то для нахождения площади можно брать синус любого угла.
III. Площадь ромба через его диагонали
Площадь ромба равна половине произведения его диагоналей.
Формула для нахождения площади ромба по его диагоналям
по сравнению с соответствующей формулой площади параллелограмма упрощается (так как диагонали ромба взаимно перпендикулярны, а синус прямого угла равен единице).

IV. Площадь ромба через радиус вписанной окружности
Площадь ромба равна произведению его полупериметра на радиус вписанной окружности.
Формула для нахождения площади ромба через радиус вписанной окружности
аналогов среди формул для нахождения площади параллелограмма не имеет (поскольку из всех параллелограммов окружность можно вписать только в ромб и квадрат).

Так как полупериметр ромба равен p=2a, формулу можно записать в виде
Калькулятор площади ромба через диагонали
Ромб — это четырехугольник, все стороны которого одинаковы. Ромб представляет собой частный случай параллелограмма, а квадрат — частный случай ромба. Следовательно, каждый квадрат — это ромб, а каждый ромб — параллелограмм.
Геометрия ромба
Термин «ромб» с греческого языка означает «бубен», который в древности выполняли в виде четырехугольника, а не круга. Ромб — равносторонний параллелограмм с неравными углами. Любой равносторонний четырехугольник, который имеет два острых и два тупых угла может называться ромбом. Таким образом, ромб в отличие от квадрата является косоугольником. Параллелограмм будет считаться ромбом, если фигура соответствует хотя бы одному из условий:
Данная фигура в своей классической форме не часто встречается в реальной жизни. Чаще всего ромбы можно найти в металлообработке: пластины резцов различных инструментов имеют именно ромбовидную форму. Кроме того, ромбические элементы встречаются в архитектуре и строительстве, а наиболее очевидным примером реального ромба является тротуарная плитка. Встречая ромбы в реальности, вам может понадобиться определить площадь данной фигуры для решения практических задач.
Площадь ромба
Площадь ромба — это плоскость, ограниченная периметром фигуры. Площадь такого четырехугольника можно найти шестью способами, используя для расчетов такие параметры как величины углов, длины сторон или диагоналей. Наиболее простая формула для определения площади ромбовидной фигуры оперирует диагоналями. Диагональ ромба — это отрезок, который соединяет вершины противоположных углов косоугольника. Зная длину диагоналей ромба, вы можете вычислить площадь по следующей формуле:
Для определения площади ромба вы можете использовать наш онлайн-сервис, который позволяет найти не только площадь или периметр фигуры, но и определяет ее углы, длину сторон и высоту. Для вычислений вам потребуется ввести в форму два параметра на выбор:
Зная эти два значения, программа рассчитает все остальные свойства ромба, которые могут вам понадобиться при решении практических задач. Рассмотрим пару примеров.
Примеры из реальной жизни
Плитка
Ранее мы выяснили, что тротуарная плитка — это самый банальный пример ромбических фигур в реальной жизни. Допустим, есть участок, который вы хотите замостить такой плиткой. Для определения необходимого количества плитки, которое нужно закупить, вам потребуется узнать два параметра: площадь участка и площадь одного элемента тротуарного покрытия. Пусть площадь участка составляет 20 квадратных метров, а диагонали плитки равны 20 см и 10 см. Для правильного расчета необходимо выразить длину диагоналей в метрах (0,2 и 0,1 м) и ввести их в поля «Диагонали». Вы получите результат в виде:
Следовательно, площадь одного элемента составляет 0,01 квадратных метров, и вам понадобится 2 000 маленьких ромбов для обустройства участка.
Геральдика
Большая часть гербов исполняется на ромбовидных геральдических щитах. Если вы захотите сделать собственный ромбовидный герб для фестиваля исторической реконструкции, то вам понадобится узнать, сколько ткани нужно для его создания. Вы можете прикинуть только длину стороны и высоту ромба. Пусть высота фигуры составляет 0,3 м, а сторона — 0,5 м. Тогда площадь герба будет равна:
Таким образом, для создания герба вам понадобится 0,15 квадратных метров ткани.
Заключение
Ромб не занимает в реальной жизни человека значимое место: фигура встречается нечасто, в основном в машиностроении, архитектуре и дизайне. Для решения практических задач или школьных заданий вы можете воспользоваться онлайн-калькулятором, который мгновенно выдаст вам не только правильный результат, но и вычислит углы, стороны и высоту ромба.
Простые формулы площади ромба!
В статье рассмотрим формулу площади ромба и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам.
Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.
Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath.ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).
Ромб обладает следующими свойствами:
— у ромба параллельные углы равные,
— сложение двух соседних углов равно 180 градусам,
— Пересечение диагоналей под углом в 90 градусов,
— Биссектрисами ромба, приходятся его же диагонали,
— Диагональ при пересечении делится на равные части.
Ромб обладает следующими признаками:
Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.
Так как в ромбе все стороны одинаковы периметр находится по следующей формуле:
Р=4а
Площадь ромба формула
Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.
С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.
Очень просто в решении и не забудется.
Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение.
Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.
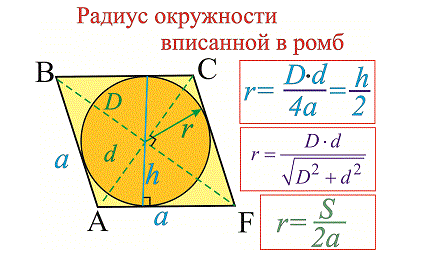
Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.
Для этого так же существует несколько формул:
В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты ( r=h/2).
Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.
В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
По собственному плачевному опыту могу сказать, что свойства ромба нужно выучить на зубок, иначе потом сложно доказывать решение. Знать знаешь, а как доказать не знаешь.
До этой статьи я только одну площадь ромба знал, а оказывается их целых три в природе существует. Обязательно допишу себе в блокнотик, поступать то все равно на физ-мат.