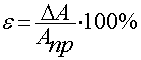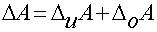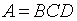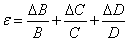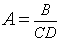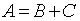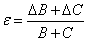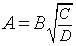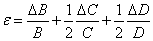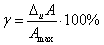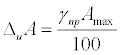как узнать погрешность измерения в физике

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник

Физика. Информатика. Портфолио.

Нашёл ошибку!?

Кто здесь?

Сейчас на сайте 46 гостей и нет пользователей

Последние слова

Информатика

Глобус

Статистика

Как определять погрешность измерений (учебник Физика 10)

1. Как определять погрешности измерений.

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

А_пр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.

ΔА — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_ИА — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1).

Δ₀А — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения); она равна в большинстве случаев половине цены деления, при измерении времени — цене деления секундомера или часов.

Абсолютные инструментальные погрешности средств измерений

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔА = 0,17 ≈ 0,2); числовое значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А = 10,332 ≈ 10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, обычно отличаются друг от друга. В этом случае А_пр находят как среднее арифметическое значение всех измерений, а погрешность ΔА (ее называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. Для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.

Формулы для вычисления относительной погрешности косвенных измерений

№	Формула для физической величины	Формула для относительной погрешности
1
2
3
4

Абсолютная погрешность косвенных измерений определяется по формуле ΔА = А_прε (ε выражается десятичной дробью).

2. О классе точности электроизмерительных приборов.

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иА от всей шкалы прибора (A_max):

Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (А_mах), определяют абсолютную погрешность Δ_иА измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений.

1. Записать результаты измерений в виде двойных неравенств:

Источник

Физика. 10 класс

Вычисление погрешностей измерений

Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.

Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.

Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.

Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ_иx + Δ_оx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.

Абсолютная инструментальная погрешность Δ_иx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.

Абсолютная погрешность отсчёта Δ_оx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.

Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:

Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:

Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.

Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.

Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.

Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.

Источник

§ 5. Точность и погрешность измерений

Всякое измерение может быть выполнено с большей или меньшей точностью.

В качестве примера рассмотрим измерение длины ручки демонстрационным метром с сантиметровыми делениями (рис. 14).

Вначале определим цену деления линейки. Она будет равна 1 см.

Если верхний конец ручки совместить с нулевым штрихом, то нижний будет находиться между 11 и 12 штрихами, но ближе к 11.

Какое же из этих двух значений следует принять за длину ручки? Очевидно, то, которое ближе к истинному значению, т. е. 11 см.

Считая, что длина ручки 11 см, мы допустили неточность, так как ручка чуть длиннее 11 см.

В физике допускаемую при измерении неточность называют погрешностью измерений.

Погрешность измерения не может быть больше цены деления шкалы измерительного прибора.

В нашем случае погрешность измерения ручки не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.

В этом случае длина ручки окажется равной 11,2 см.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и наших органов чувств при любом измерении получаются лишь приближённые значения, несколько большие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что погрешность измерений равна половине цены деления шкалы измерительного прибора.

Измерим длину карандаша. Нулевую отметку линейки совместим с одним концом карандаша, а другой её конец окажется вблизи 14 см. Цена деления линейки 1 мм, тогда погрешность измерения будет равна 0,5 мм или 0,05 см.

Следовательно, длину карандаша можно записать в виде

где I — длина карандаша.

Истинное значение длины карандаша находится в интервале от 13,95 см до 14,05 см.

При записи величин, с учётом погрешности, следует пользоваться формулой

где А — измеряемая величина, а — результат измерений, Δа — погрешность измерений (Δ — греч. буква «дельта»).

Вопросы

1. Как понимать выражение «измерить длину с точностью до 1 мм»?
2. Можно ли линейкой, имеющей сантиметровые деления, измерить длину с точностью до 1 мм?
3. Какова связь точности измерений с ценой деления шкалы прибора?
4. Какой формулой необходимо пользоваться при записи физических величин с учётом погрешности?

Задание

1. Измерьте линейкой с миллиметровыми делениями длину и ширину вашего учебника. Запишите результаты с учётом погрешности измерения.

2. Пользуясь рисунком 11, б, определите погрешность измерения термометра.

3. Измерьте линейкой с миллиметровыми делениями длину и высоту картины Л. да Винчи (рис. 15). Запишите результаты измерений с учётом погрешности. Используя Интернет, найдите название картины, её истинный размер и определите масштаб, в котором картина представлена в учебнике.

Источник