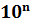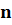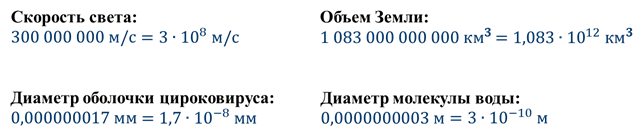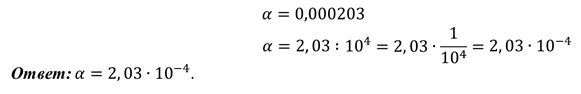как узнать порядок числа
Математика
Числа, подобно единицам, также разделяются на порядки. Так, первые десять чисел называют числами первого порядка. Числа от десяти до ста называют числами второго порядка, от ста до тысячи — числами третьего порядка и т. д.
Названия чисел. При помощи указанных единиц различного порядка мы получаем названия всех остальных чисел. Так, числа, состоящие из одной, двух, трех … единиц второго порядка, или, что то же, одного, двух, трех … десятков, мы называем десять, двадцать (два десять), тридцать, сорок, пятьдесят, шестьдесят, семьдесят, восемьдесят, девяносто. Присоединяя к этим числам девять чисел первого порядка, мы получаем все числа второго порядка. Так, присоединяя к числу десять все числа первого порядка, мы получаем все числа между десятью и двадцатью: одиннадцать, двенадцать (два на десять), тринадцать, четырнадцать, пятнадцать, шестнадцать, семнадцать, восемнадцать, девятнадцать. Присоединяя к двадцати девять чисел первого порядка, получим все числа между двадцатью и тридцатью: двадцать один, двадцать два и т. д. Наибольшее число второго порядка есть девяносто девять.
Десять десятков образуют сотню или сто, единицу третьего порядка. Числа, состоящие из одной или нескольких единиц третьего порядка, мы называем: сто, двести, триста, четыреста, пятьсот, шестьсот, семьсот, восемьсот, девятьсот.
Присоединяя к этим числам все числа первого и второго порядка, мы получаем все числа третьего порядка, например, восемьсот сорок пять, девятьсот четыре. Наибольшее число третьего порядка есть девятьсот девяносто девять.
Десять сот образуют тысячу — единицу четвертого порядка. Повторяя тысячу один, два и т. д. раз, образуем числа: тысяча, две тысячи, три тысячи и т. д. Присоединяя к этим числам все числа первого, второго и третьего порядков, образуем все числа четвертого порядка и т. д.
Десятичная система. Систему счисления, в которой каждые десять единиц низшего образуют единицу следующего высшего порядка, называют десятичною. Она принята в настоящее время всеми образованными народами.
Основание системы. Число десять называется основанием системы. В основе ее лежит число десять.
Полагают, что число десять принято за основание потому, что первоначально люди считают обыкновенно по пальцам.
Пример. Шесть миллионов пятьсот семь тысяч двести семь есть число седьмого порядка. Оно состоит из шести единиц седьмого прядка (шесть миллионов), к которому присоединено число шестого порядка (пятьсот семь тысяч двести семь).
Число шестого порядка состоит из пяти единиц шестого порядка (пятьсот тысяч), к которому присоединено число четвертого порядка (семь тысяч двести семь).
Число четвертого порядка состоит из семи единиц четвертого порядка (семь тысяч), к которому присоединено число третьего порядка (двести семь).
Число третьего порядка состоит из двух единиц третьего порядка (двести), к которому присоединяется число первого порядка (семь).
Число семь состоит из семи простых единиц.
Всякое число содержится между двумя единицами различных порядков. Всякое число более единицы одного порядка и менее единицы следующего высшего порядка. Так, число триста сорок семь более ста и менее тысячи.
Стандартная форма записи числа, мантисса числа, порядок числа
Положительное число, записанное в стандартной форме, имеет вид
,
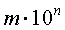
Число m является натуральным числом или десятичной дробью, удовлетворяет неравенству
,
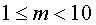
и называется мантиссой числа, записанного в стандартной форме.
Число n является целым числом (положительным, отрицательным или нулем) и называется порядком числа, записанного в стандартной форме.
Например, число 3251 в стандартной форме записывается так:
,
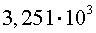
Здесь число 3,251 является мантиссой, а число 3 является порядком.
Стандартная форма записи числа часто используется в научных расчетах и очень удобна для сравнения чисел.
Для того, чтобы сравнить два числа, записанных в стандартной форме, нужно сначала сравнить их порядки. Большим будет то число, порядок которого больше. Если же порядки сравниваемых чисел одинаковы, то нужно сравнить мантиссы чисел. Большим в этом случае будет то число, у которого мантисса больше.
Например, если сравнить между собой записанные в стандартной форме числа
и 
,
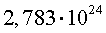
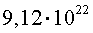
то, очевидно, первое число больше второго, поскольку у него порядок больше.
Если же сравнить между собой числа
и 
,
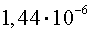
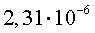
то, очевидно, что второе число больше, чем первое, поскольку порядки у этих чисел совпадают, а мантисса у второго числа больше.
Числовая последовательность
Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: \(2; 4; 6; 8; 10. \) А правило «первое число равно \(3\), а каждое следующее число в два раза больше предыдущего» формирует последовательность: \(3; 6; 12; 24; 48. \)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами (или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности \(3; 6; 12; 24; 48…\) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность \(3; 6; 12; 24; 48…\) обозначить как \(a_n\), то можно записать, что \(a_1=3\), \(a_2=6\), \(a_3=12\), \(a_4=24\) и так далее.
порядковый номер элемента
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
— I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Отметим, что последовательности в начале статьи заданы именно словесным способом.
— II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: \(b_n=\frac
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: \(a_n=8+5n-n^2\). Вычислите \(a_9\).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер \(n=9\). Подставляем в формулу: \(a_9=8+5·9-9^2=8+45-81=-28\).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: \(c_1=4\), \(c_
Решение: Первый член нам известен: \(c_1=4\).
Второй мы получим, подставив в формулу вместо \(n\) единицу: \(c_<1+1>=c_1+3\)
\(c_2=c_1+3=4+3=7\)
Третий (\(n=2\)): \(c_<2+1>=c_2+3 \)
\(c_3=c_2+3=7+3=10\).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула \(c_
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента \(z_1=2;\) \(z_2=5\). Так же известна формула следующего элемента \(z_
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
Последовательность на данный момент:
Так как формула дана для элемента с номером \(n+2\), то чтобы найти \(z_3\) нужно подставлять вместо \(n\) единицу:
\(z_<1+2>=3z_<1+1>-z_1\)
\(z_3=3z_2-z_1=3·5-2=13\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | ? | ? | \(. \) |
\(z_<2+2>=3z_<2+1>-z_2\)
\(z_4=3z_3-z_2=3·13-5=34\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | \(34\) | ? | \(. \) |
\(z_<3+2>=3z_<3+1>-z_3\)
\(z_5=3z_4-z_3=3·34-13=89\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | \(34\) | \(89\) | \(. \) |
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности \(a_n=n^2-n\):
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
\(a_2=2^2-2=2\) – тоже не то.
Нужный элемент найден.
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
Если число \(3\) – член последовательности, то значит при некотором значении \(n\), формула \(\frac<51+2n>
Подставляем тройку вместо \(a_n\).
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Стандартный вид числа
Урок 36. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Стандартный вид числа»
Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Стандартным видом числа 
называют его запись в виде: 
, где 
и 
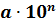
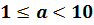
– целое число.
Число называется порядком числа .
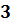
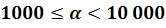
Если порядок числа равен 
, то это означает, что 
.
Если порядок числа равен 
, то это означает, что 
.
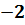
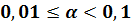
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
, где и – целое число
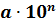
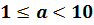
По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2. полученное число умножить на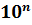 
, где подбирается так, чтобы произведение было равно данному числу.
Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Задание: запишите число в стандартном виде.
Задание: запишите в стандартном виде число, равное значению произведения х и у.
Стандартным видом числа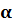 
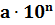
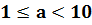
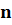
называют его запись в виде: 
, где 
и 
– целое число.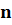
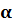
Число называется порядком числа .
Для того, чтобы привести число к стандартному виду, надо перенести в нём запятую так, чтобы она была сразу после первой значащей цифры, и полученное число умножить на 
, где подбирается так, чтобы произведение было равно данному числу.