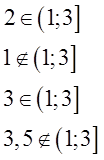как узнать принадлежит ли число промежутку

Простейшая проверка принадлежности натурального числа промежутку

Как математически грамотно (желательно на Java) одним условием проверить, принадлежит ли натуральное число b отрезку [a, c], где a и c так же натуральные числа? Условие должно выполниться, например, при таких значениях a, b, и c соответственно: (1, 2, 3), (5, 7, 10), (17, 25, 25), но не должно выполниться, например, при таких значениях a, b, и c соответственно: (2, 1, 3), (17, 25, 24). Условие должно быть одно, использовать логические операторы (такие как &&, ||, и т.п.) нельзя.

3 ответа 3

Если точка лежит внутри отрезка, то сумма расстояний от этой точки до крайних точек отрезка всегда равна расстоянию между крайними точками. Если точка лежит вне отрезка, тогда сумма расстояний всегда будет больше. Иллюстрация:

Как известно, расстояние между двумя точками на отрезке – это модуль разности координат этих точек.

Отсюда получаем условие:

Я придумал такой вариант

Применительно к данной задаче, финальное условие будет выглядеть так:

Полный код программы, с которым можно поиграться:

Минус данного решения в том, что при больших числах возможно переполнение на умножении.

Источник

Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)

Что такое числовая прямая? Что такое координатная прямая?

С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)

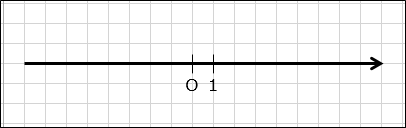
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:

1) Начало отсчёта или начало координат (точку О);

2) Положительное направление (стрелочкой);

3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).

Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)

Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)

А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)

Что такое числовой промежуток? Виды числовых промежутков.

В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?

Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!

Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)

Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)

Соответственно, и числовые промежутки в математике бывают разных видов.

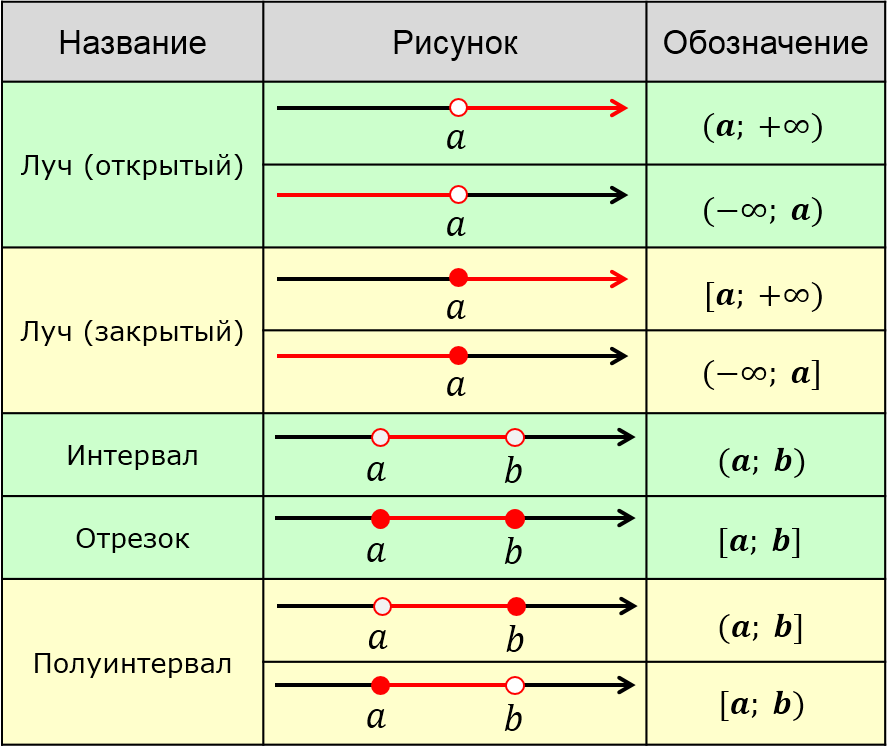
Вот они, эти виды (подкрашены красным цветом):

Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф «∞», да ещё и со знаками плюс/минус, круглые и квадратные скобочки.

Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)

Граничные точки

Я разгадала знак бесконечность… (Земфира)

А может ли числовой промежуток в каком-то направлении быть неограниченным?

А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок «∞«. Значок этот так и называется — «бесконечность». Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.

Кружочки и скобочки…

Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?

Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!

Запоминаем:

Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками «(» или «)».

Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой «[» или «]».

Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят «числовой промежуток такой-то…», без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто «промежуток». Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)

Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?

Читаем числовые промежутки и рисуем их на оси!

С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.

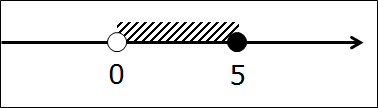
Например, задан числовой промежуток (0; 5].

Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.

Читаем (и пишем) именно в таком порядке — от левой границы до правой.

Левая граница (т.е. число 0) соседствует с круглой скобкой «(«, о чём нам и говорят слова «не включая». Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…

Пятёрка же — напротив, соседствует с квадратной скобкой «]», что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом «включая» в словесной расшифровке.

А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.

Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить! 😉 Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…

Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?

Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.

Вариант второй рассмотрим на следующем примере.

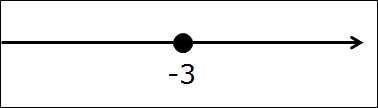
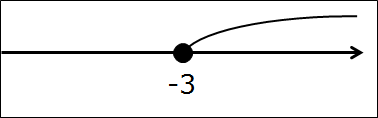
В этот раз дан промежуток такой: [-3; +∞).

Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!

Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах «включая минус три…» и не продолжил мысль гениальными словами «…и не включая плюс бесконечность»?

Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: «до плюс бесконечности». Или «до минус бесконечности». И всё.

А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:

И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:

Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.

Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)

Вот так рисуются числовые промежутки на оси.

Входит и выходит… ))

А какая нам разница, входит число в указанный промежуток или не входит?

Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:

За этими странными значками скрываются безобидные слова «принадлежит» и «не принадлежит».

Возьмём, к примеру, промежуток (1; 3].

Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…

Математически, с помощью значков принадлежности, эти факты можно записать вот так:

А словами можно прочитать вот так:

Два принадлежит промежутку от одного (не включая) до трёх (включая).

Один не принадлежит промежутку от одного (не включая) до трёх (включая).

В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.

Источник

Таблица числовых промежутков: виды, обозначения, изображения

Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.

Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.

Виды числовых промежутков

Каждый числовой промежуток характеризуется:

Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.

Произведем описание числовых промежутков с выше указанными сторонами:

Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x a включает в себя точки, которые расположены левее, а для x > a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.

Рассмотрим несколько примеров.

Для наглядного примера зададим числовой луч.

Рассмотрим рисунок, приведенный ниже.

Таблица числовых промежутков

Промежутки могут быть изображены в виде:

Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.

Источник

Определить какому промежутку принадлежит введенное число

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Определить, принадлежит ли заданное число промежутку
Определить, принадлежит ли заданное число отрезку / промежутку Помогите написать код!

Определить, принадлежит ли введенное число заданному массиву
Подскажите пожалуйста, у меня такое задание, есть массив, пользователь вводит с клавиатуры число и.

Определить, принадлежит ли введенное число арифметической прогрессии с введенными начальным членом и шагом
Здравствуйте люди добрые,учусь на первом курсе и пока тяжело всё идёт. Столкнулся с проблемой для.

Определить, принадлежит ли введенное число арифметической прогрессии с введенными начальным членом и шагом
Вводятся начальный член и шаг арифметической прогрессии. Вводится также число. Определить.

Решение

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Определить, к какому элементу массива принадлежит считываемый символ
Добрый день, уважаемые форумчане! подскажите пожалуйста есть массив const int M=8; char*.

Проверить принадлежит ли введенное число заданному диапазону
Введіть з клавіатури два числадля більшого з них числа перевірте чи знаходиться воно вдіапазоні від.

Составить условное выражение, принадлежит ли введенное число указанным диапазонам
Задание 1 Составить условное выражение, принадлежит ли A (вводится с клавиатуры) диапазону (2;5].

Цикл: Показать к какому номеру относится введенное число.
Такая проблема! необходимо с помощью цикла вычислить от 1 до 10 (№1 ) от 10 до 20 (№2 ) от 20.

Какому промежутку принадлежит число в степени
Всем привет. Такая ситуация: решал систему неравенств, ввёл новую переменную и получил.

Источник

Как узнать принадлежит ли число промежутку

Какому промежутку принадлежит число

В ответе укажите номер правильного варианта.

Возведём в квадрат числа 4, 5, 6, 7, 8:

Число 53 лежит между числами 49 и 64, поэтому принадлежит промежутку

Правильный ответ указан под номером 4.

Приведём другое решение.

Какому из данных промежутков принадлежит число

В ответе укажите номер правильного варианта.

Переведём в десятичную дробь с точностью до второго знака после запятой при помощи деления в столбик, получим:

Число 0,55 принадлежит промежутку [0,5;0,6].

Правильный ответ указан под номером: 1.

Какому из данных промежутков принадлежит число ?

Разделим 7 на 11 в столбик, получим 0,636363. Это число лежит в промежутке [0,6; 0,7].

Правильный ответ указан под номером 3.

Какое из данных чисел принадлежит промежутку [6; 7]?

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Возведём все числа в квадрат:

Заметим, что следовательно, Таким образом, число принадлежит промежутку [6; 7].

Правильный ответ указан под номером: 4.

Какому из данных промежутков принадлежит число ?

Разделим 2 на 9 в столбик, получим 0,2222. Это число лежит в промежутке [0,2; 0,3].

Правильный ответ указан под номером 2.

Какое из данных чисел принадлежит промежутку [7; 8]?

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Возведём все числа в квадрат:

Заметим, что следовательно, Таким образом, число принадлежит промежутку [7; 8].

Правильный ответ указан под номером 4.

Какое из данных чисел принадлежит промежутку [7; 8]?

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Возведём все числа в квадрат:

Заметим, что следовательно, Таким образом, число принадлежит промежутку [7; 8].

Правильный ответ указан под номером: 4.

Какое из данных ниже чисел принадлежит отрезку [3; 4]?

1)

2)

3)

4)

Рассмотрим каждое из чисел:

1.

2.

3.

4.

Таким образом, третье число принадлежит отрезку [3; 4].

Какое из данных ниже чисел принадлежит отрезку [3; 4]?

1)

2)

3)

4)

Рассмотрим каждое из чисел:

1.

2.

3.

4.

Таким образом, первое число принадлежит отрезку [3; 4].

Аналоги к заданию № 369728: 369796 369825 369854 Все

Какое из данных ниже чисел принадлежит отрезку [8; 9]?

1)

2)

3)

4)

Рассмотрим каждое из чисел:

1.

2.

3.

4.

Таким образом, четвёртое число принадлежит отрезку [8; 9].

Аналоги к заданию № 369728: 369796 369825 369854 Все

Какое из данных ниже чисел принадлежит отрезку [4; 5]?

1)

2)

3)

4)

Рассмотрим каждое из чисел:

1.

2.

3.

4.

Таким образом, второе число принадлежит отрезку [4;&thinsp5].

Аналоги к заданию № 369728: 369796 369825 369854 Все

Источник