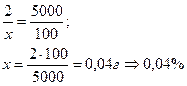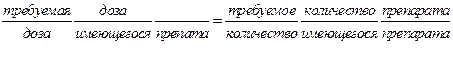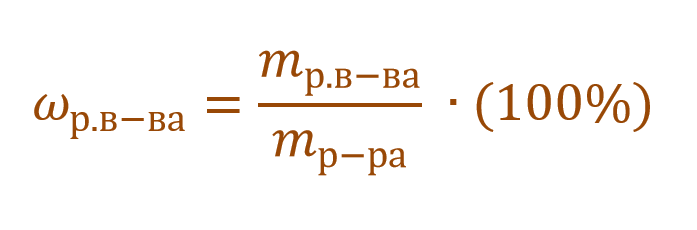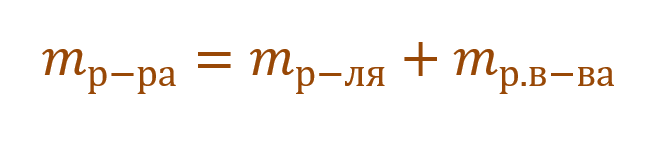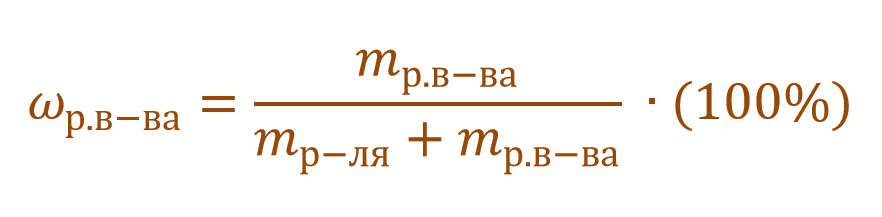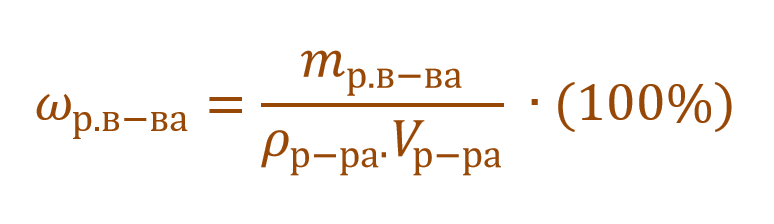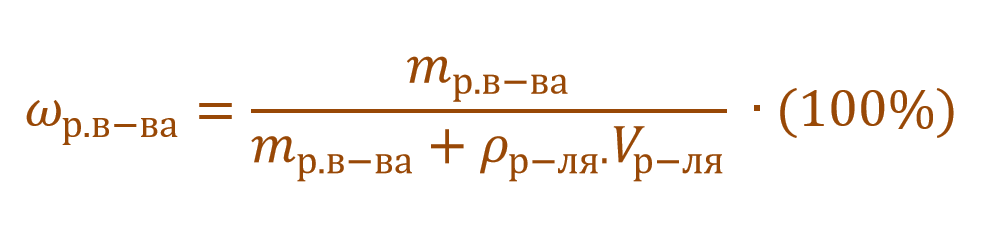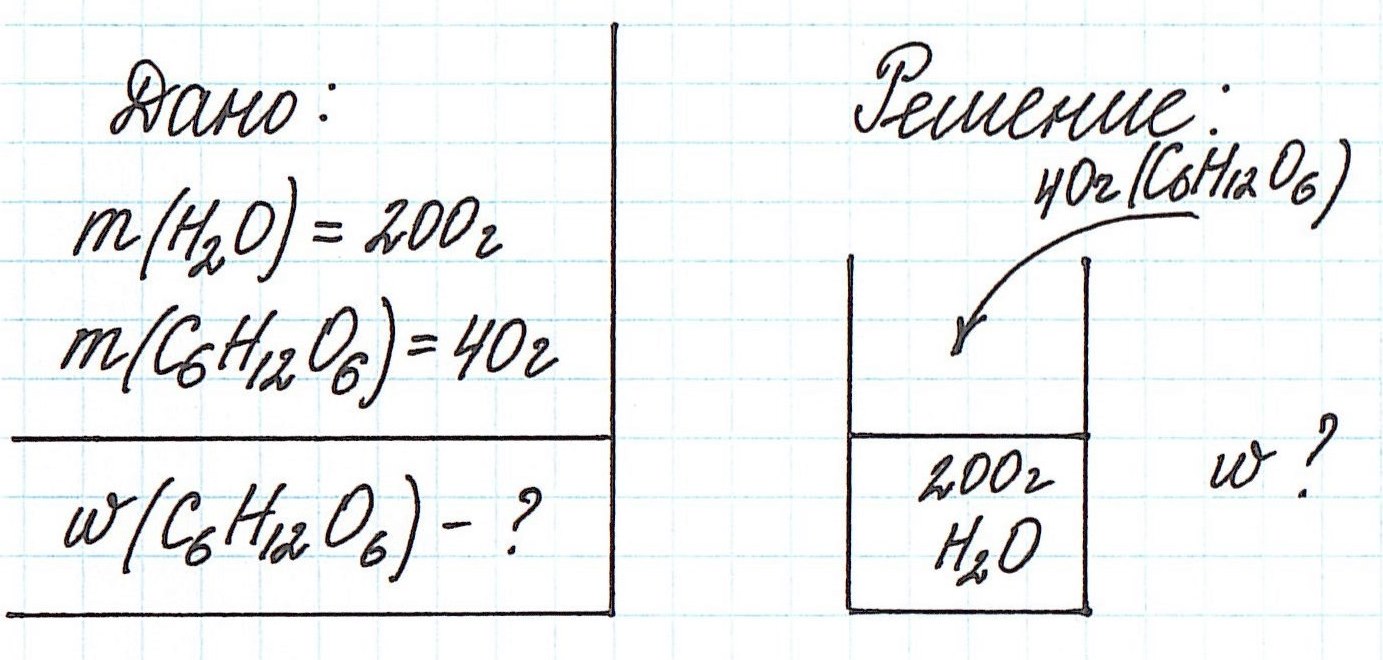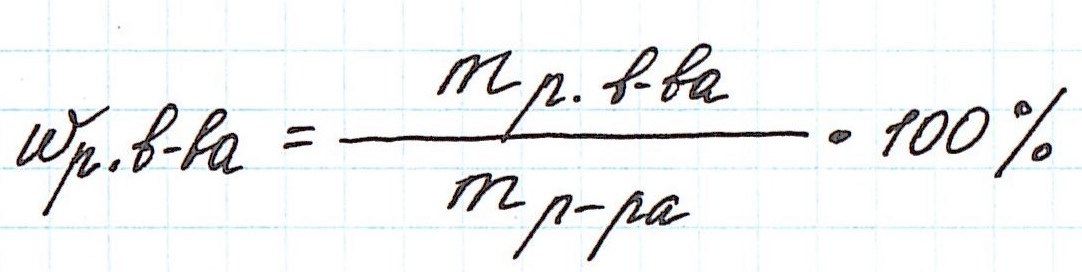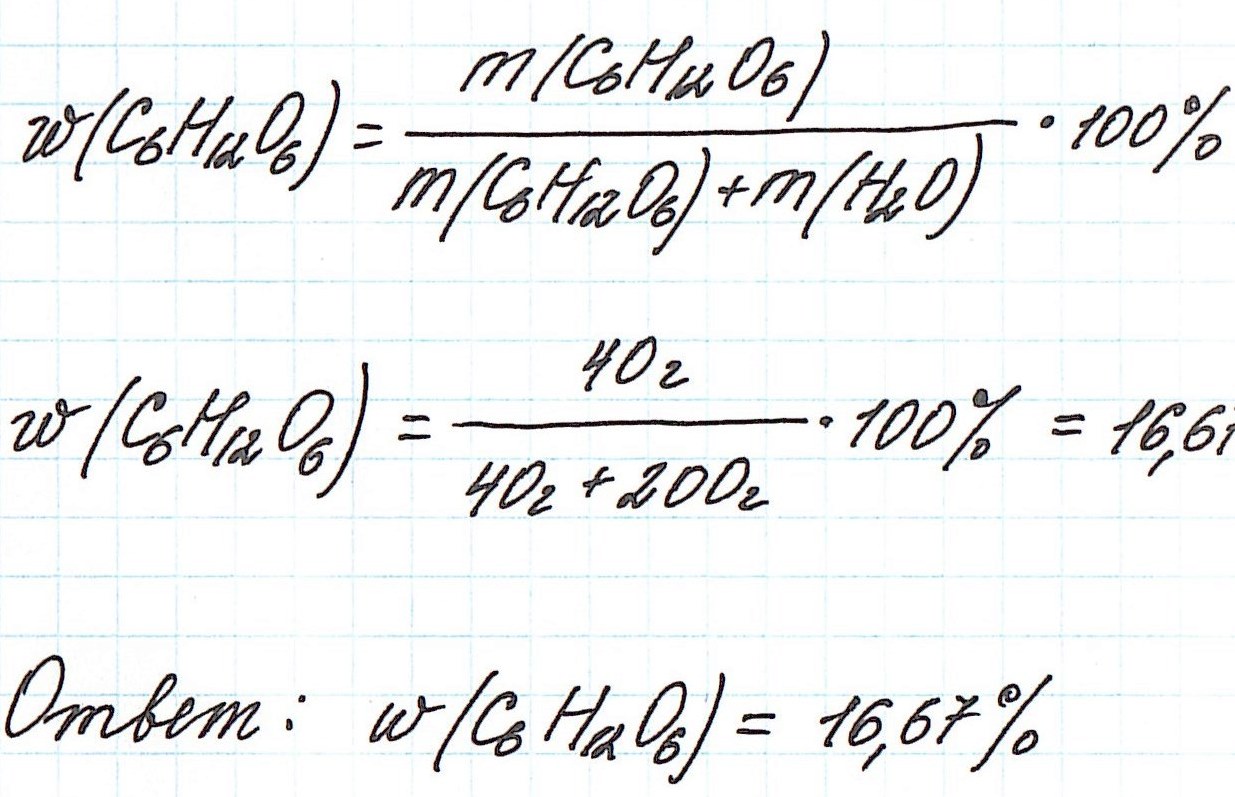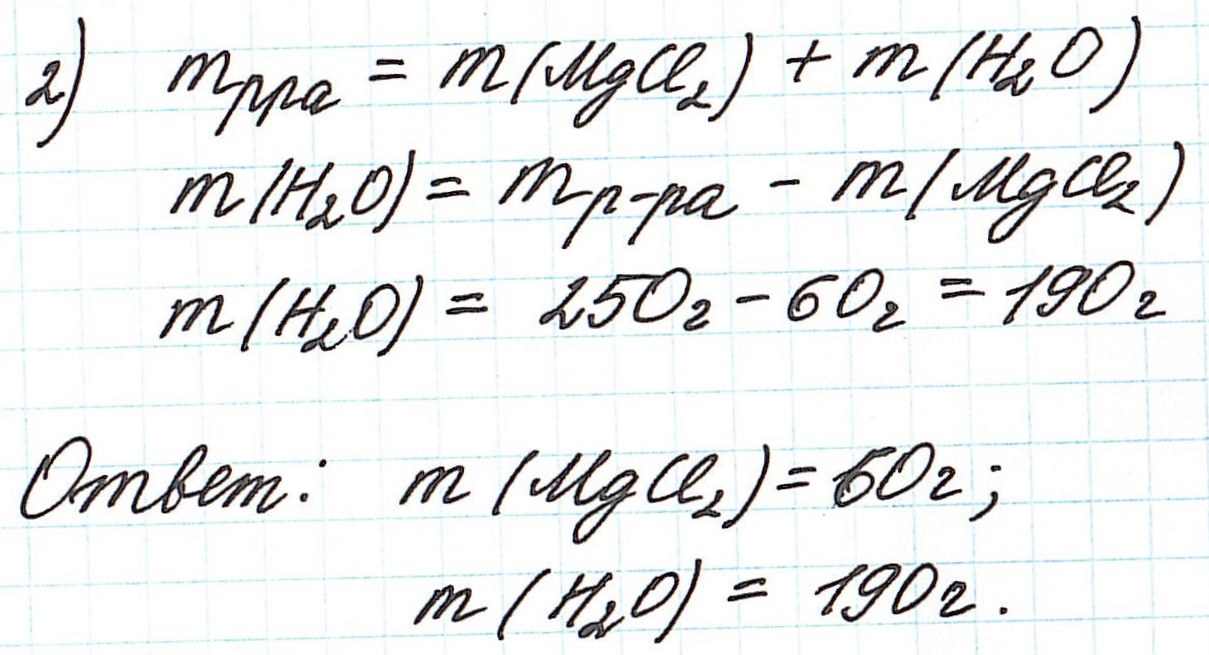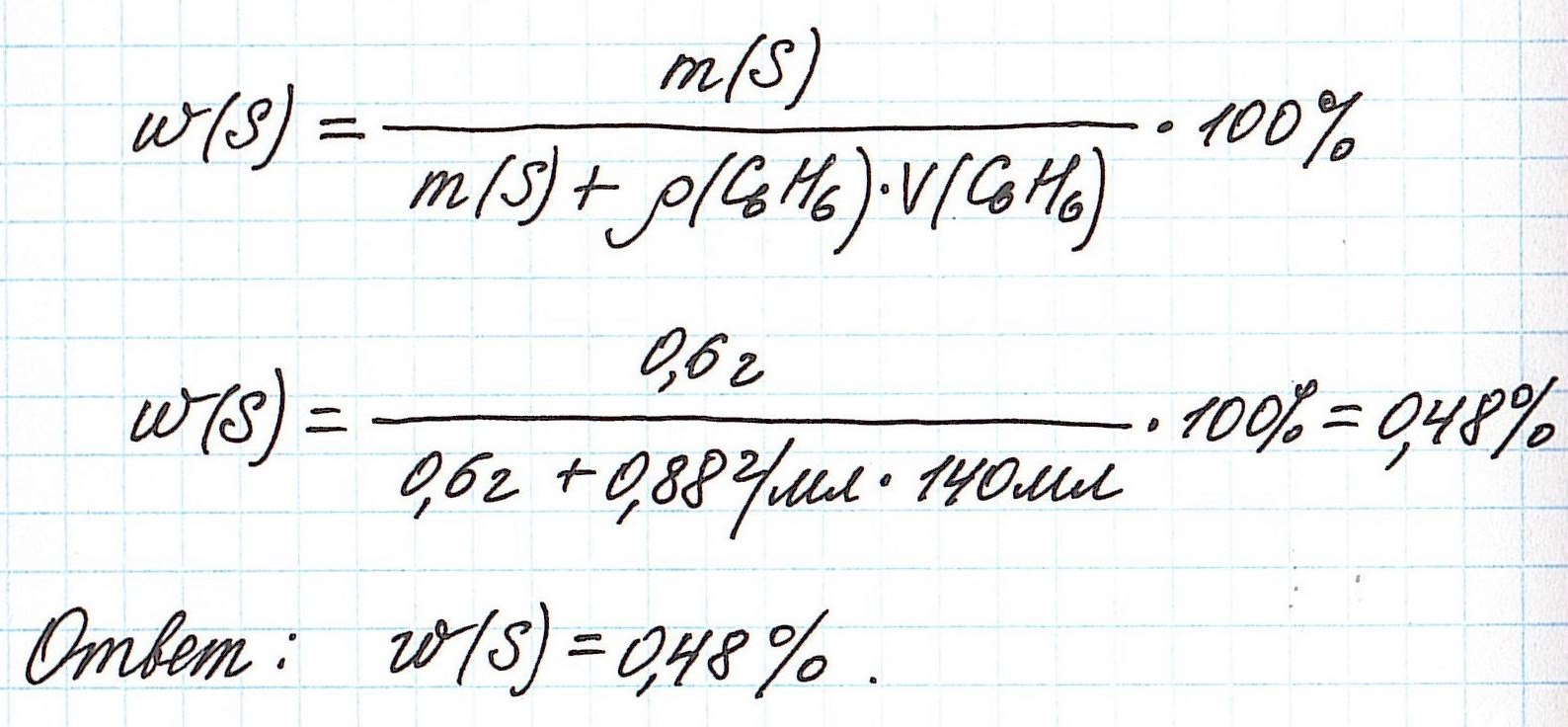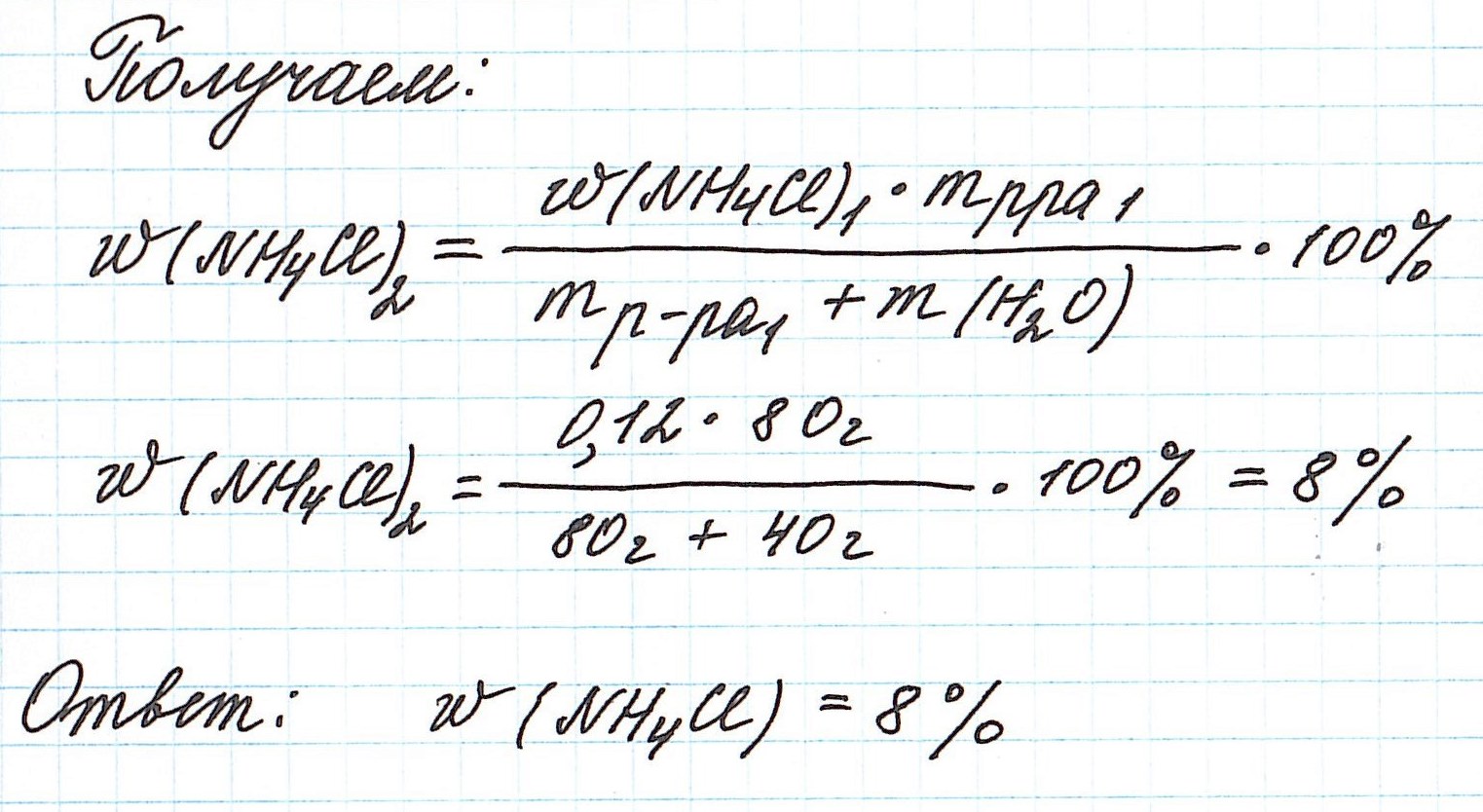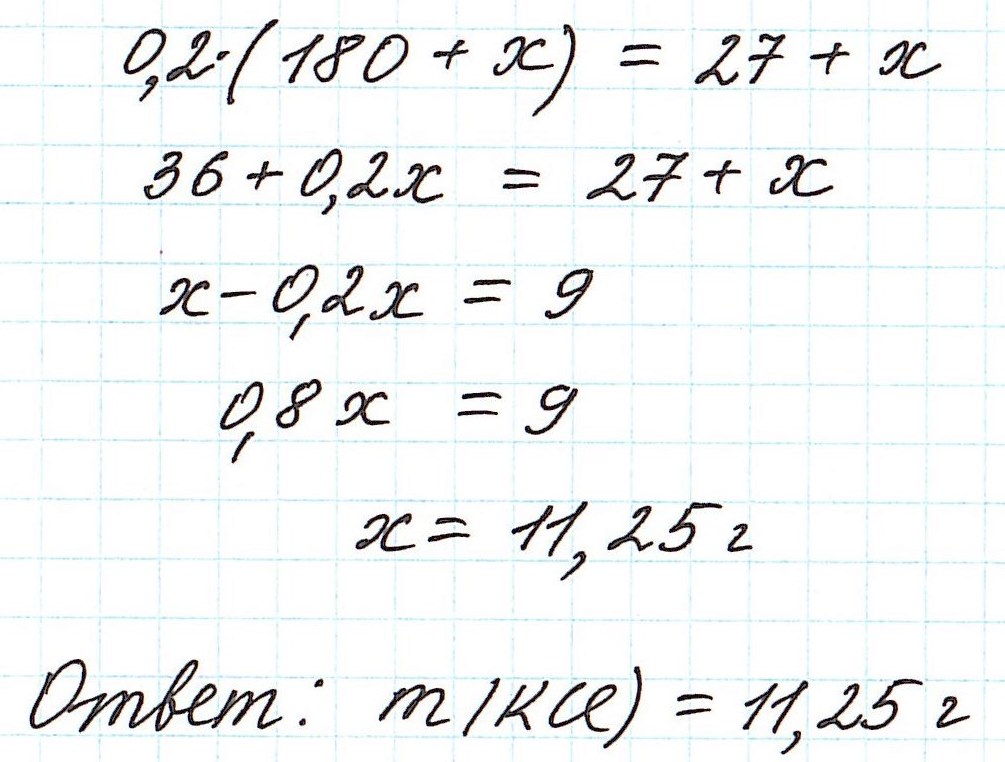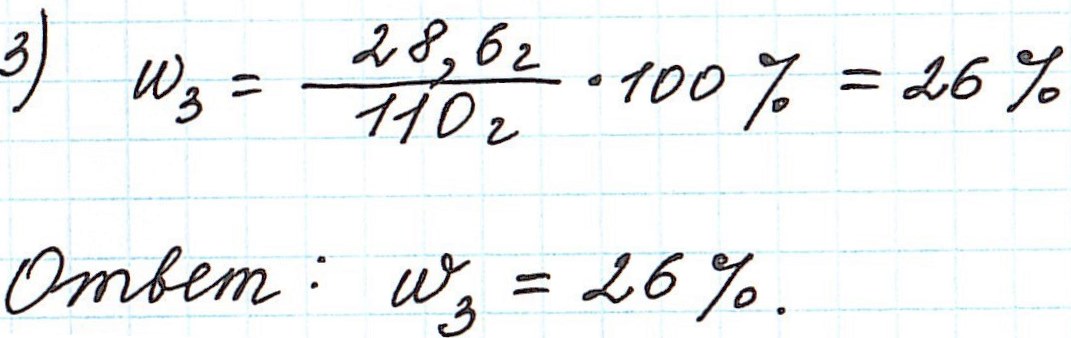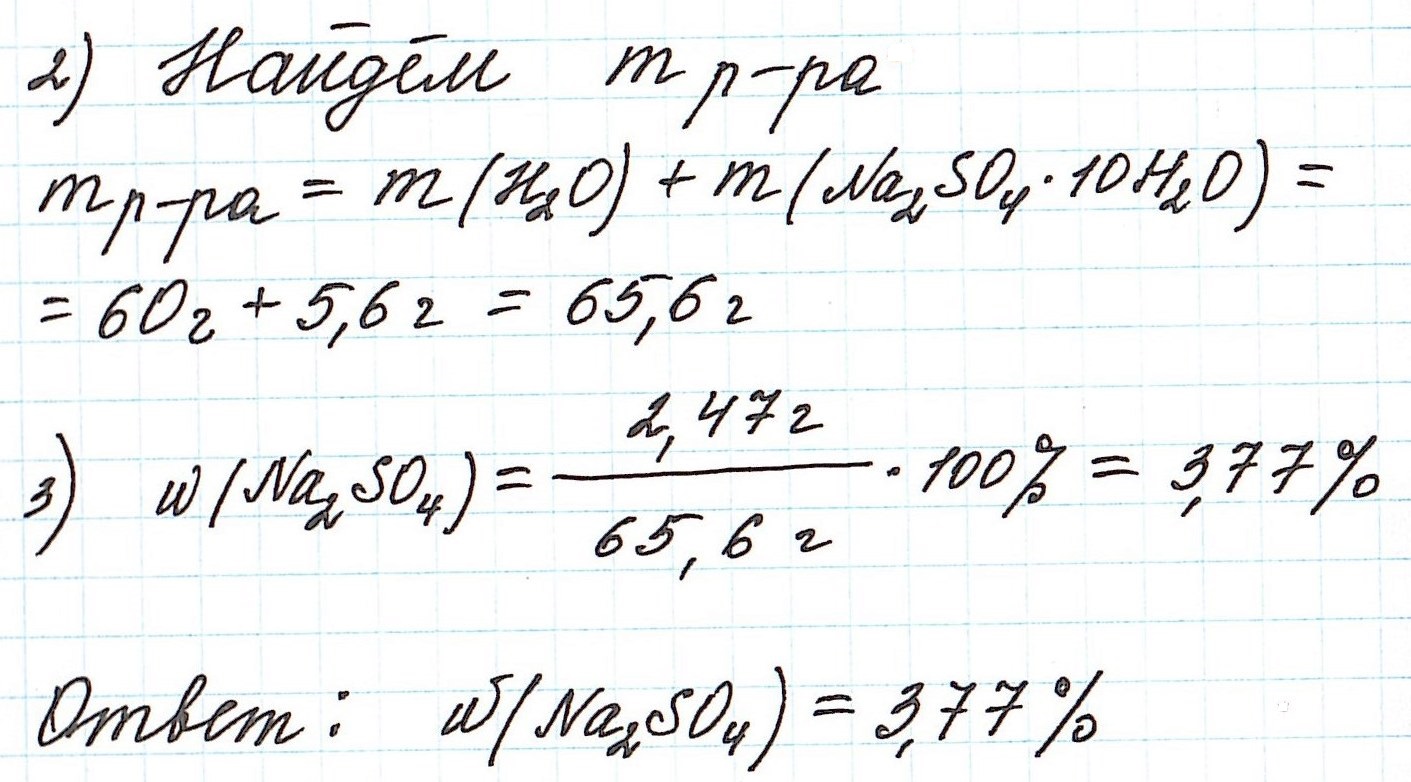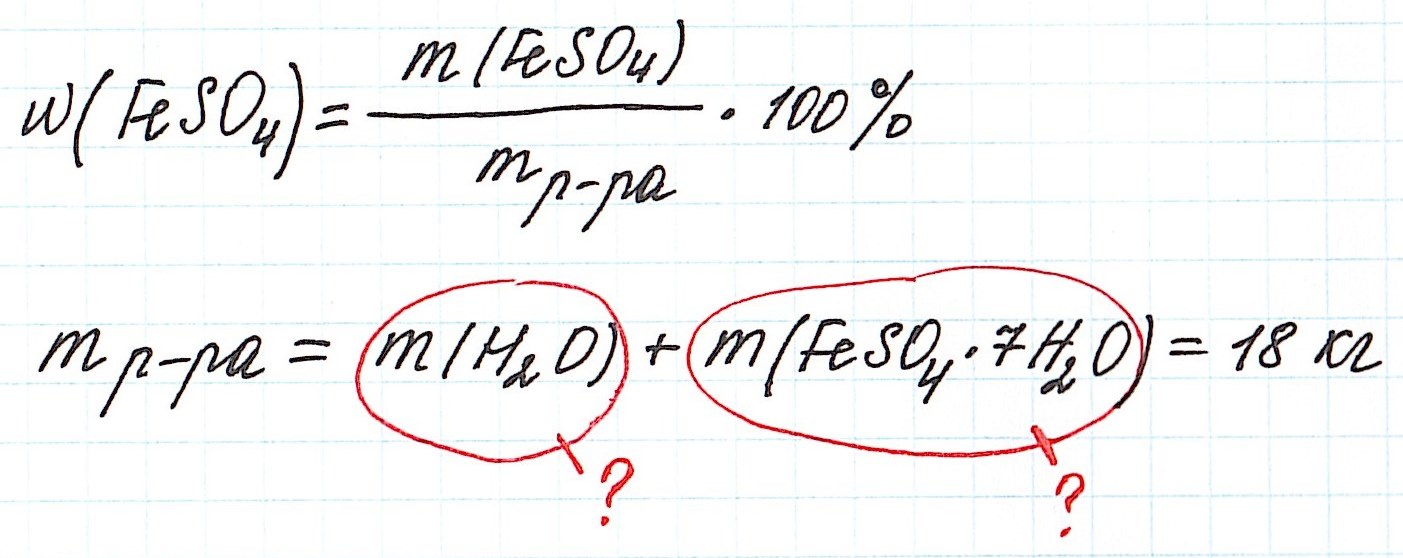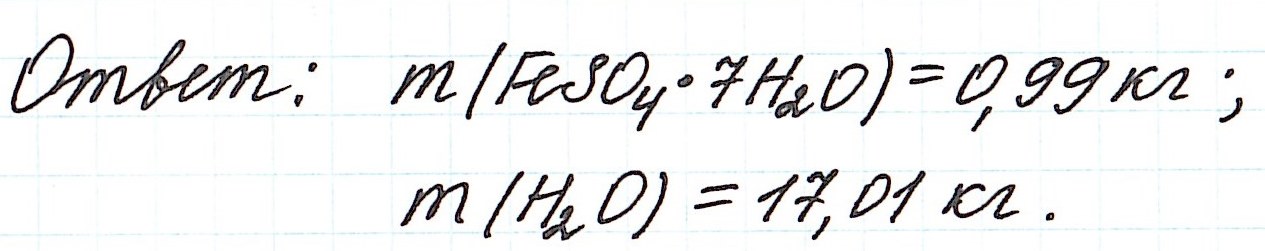как узнать процент жидкости
Как рассчитать концентрацию раствора
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество источников, использованных в этой статье: 7. Вы найдете их список внизу страницы.
Количество просмотров этой статьи: 162 474.
В химии концентрация раствора показывает, как много растворенного вещества содержится в растворителе. Согласно стандартной формуле C = m/V, где C — концентрация, m — масса растворенного вещества и V — общий объем раствора. При малых концентрациях удобнее вычислять концентрацию в миллионных долях (ppm). Во время лабораторной работы вас могут попросить также вычислить молярность, или молярную концентрацию раствора.
Совет: если необходимо использовать весы, вычтите из общей массы массу емкости, в которой находится взвешиваемая жидкость, чтобы получить правильный результат.
Совет: миллионные доли обычно используют для очень малых концентраций, когда легче записать и понять ответ в них, а не в процентах.
Совет: обычно нет необходимости учитывать объем растворенного вещества, так как он, как правило, не сильно влияет на общий объем. Однако если объем заметно изменится после того, как вы добавите растворимое вещество, используйте общий объем раствора.
Задачи на смеси и сплавы
Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
— масса раствора = масса воды + масса соли;
— масса сплава равна сумме масс металлов, входящих в этот сплав;
— масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Концентрация (процентное содержание) цинка в смеси:
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве .
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Концентрация растворов. Способы выражения концентрации растворов.
Концентрация раствора может выражаться как в безразмерных единицах (долях, процентах), так и в размерных величинах (массовых долях, молярности, титрах, мольных долях).
Способы выражения концентрации растворов.
1. Массовая доля (или процентная концентрация вещества) – это отношение массы растворенного вещества m к общей массе раствора. Для бинарного раствора, состоящего из растворённого вещества и растворителя:

ω – массовая доля растворенного вещества;
mв-ва – масса растворённого вещества;
Массовую долю выражают в долях от единицы или в процентах.
2. Молярная концентрация или молярность – это количество молей растворённого вещества в одном литре раствора V:

C – молярная концентрация растворённого вещества, моль/л (возможно также обозначение М, например, 0,2 М HCl);
n – количество растворенного вещества, моль;
V – объём раствора, л.
Раствор называют молярным или одномолярным, если в 1 литре раствора растворено 1 моль вещества, децимолярным – растворено 0,1 моля вещества, сантимолярным – растворено 0,01 моля вещества, миллимолярным – растворено 0,001 моля вещества.
3. Моляльная концентрация (моляльность) раствора С(x) показывает количество молей n растворенного вещества в 1 кг растворителя m:

С (x) – моляльность, моль/кг;
n – количество растворенного вещества, моль;
4. Титр – содержание вещества в граммах в 1 мл раствора:

T – титр растворённого вещества, г/мл;
mв-ва – масса растворенного вещества, г;
5. Мольная доля растворённого вещества – безразмерная величина, равная отношению количества растворенного вещества n к общему количеству веществ в растворе:

N – мольная доля растворённого вещества;
n – количество растворённого вещества, моль;
nр-ля – количество вещества растворителя, моль.
Сумма мольных долей должна равняться 1:
Иногда при решении задач необходимо переходить от одних единиц выражения к другим:
М(Х) – молярная масса растворенного вещества;
ρ= m/(1000V) – плотность раствора. 6. Нормальная концентрация растворов (нормальность или молярная концентрация эквивалента) – число грамм-эквивалентов данного вещества в одном литре раствора.
Грамм-эквивалент вещества – количество граммов вещества, численно равное его эквиваленту.
Эквивалент – это условная единица, равноценная одному иону водорода в кислотоно-основных реакциях или одному электрону в окислительно – восстановительных реакциях.
Для записи концентрации таких растворов используют сокращения н или N. Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.

СН – нормальная концентрация, моль-экв/л;
z – число эквивалентности;
Коэффициент растворимости – отношение массы вещества, образующего насыщенный раствор при конкретной температуре, к массе растворителя:
Расчет процентной концентрации растворов
Чтобы найти процентное выражение данного числа, нужно умножить это число на 100 (или, что одно и то же, перенести в нем запятую на 2 знака вправо).
найдем процентное выражение числа 2, для этого умножим 2 на 100% и получим 200%.
Число 0,357 = 0,357·100 = 35,7%; число 1,753 = 1,753·100 = 175,3%.
Чтобы найти число по его процентному выражению, нужно разделить процентное выражение на 100 (или, что одно и то же, перенести запятую через 2 знака влево).
Представим 25% в виде числа, для этого разделим 25% на 100 и получим 0,25.
13,5% = 0,135 (мы перенесли запятую на 2 знака влево);
2,3% =2,3:100 = 0,023; 145% = 145:100 = 1,45.
(в различных объемах жидкости)
Различают три основные задачи на проценты:
Задача №1. Найти указанный процент данного числа.
Чтобы найти указанный процент данного числа, необходимо данное число разделить на 100, и полученный результат умножить на число процентов.
Пример: В отделении за сутки в среднем расходуется 0,5кг хлорной извести. Во время генеральной уборки помещений было израсходовано 153% среднесуточного количества хлорной извести. Сколько хлорной извести израсходовал персонал отделения во время генеральной уборки помещения?
1) 0,5:100 = 0,005 (приходится на 1%)
2) 0,005·153 = 0,765 (кг) израсходовали.
Ответ: За сутки во время генеральной уборки израсходовано 0,765кг хлорной извести.
Задача №2. Найти число по данной величине указанного его процента
Чтобы найти число по данной величине указанного его процента, необходимо данную величину разделить на число процентов, и результат умножить на 100.
Вес хлорной извести в растворе составляет 10%. Сколько потребуется воды для разведения раствора, если известно, что хлорной извести взяли 0,2кг?
1) 0,2:10 = 0,02 (кг приходится на 1%)
Ответ: Потребуется 2л.
Задача №3. Найти выражение одного числа в процентах другого.
Чтобы найти выражение одного числа в процентах другого, нужно умножить первое число на 100, а затем полученный результат разделить на второе число.
За сутки отделение израсходовало 765г хлорной извести вместо среднесуточной нормы расхода 500г. На сколько процентов больше израсходовано хлорной извести?
1) 765 – 500 = 265(г) – израсходовано больше хлорной извести, чем положено по норме
3) 26500:500 = 53% составляет перерасход хлорной извести
Ответ: на 53% больше.
При изучении предметов «Фармакология», «Основы сестринского дела» вы часто сталкиваетесь с таким понятием как концентрация раствора. Что же мы подразумеваем под этим понятием?
По определению концентрации чистого вещества в растворе – это количество граммов в 100мл.
Следовательно, для расчета количества вещества в 1мл раствора необходимо имеющуюся массу чистого вещества в растворе разделить на 100.
Пример:
Рассчитать дозу сухого вещества кофеина бензола натрия на один прием при назначении на прием столовой ложки 0,5% раствора (столовая ложка = 25мл)
1) 25:100 = 0,25 (г) концентрация вещества в 1мл
2) 0,25·0,5 = 0,125 (г) доза сухого вещества в растворе
Ответ: 0,125г – доза сухого вещества в растворе.
Для решения вышеприведенных задач часто используют понятие пропорции.
Пропорция – это верное отношение 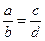
В данном отношении 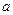
Справедливо следующее утверждение (свойство пропорции): произведение средних членов пропорции равно произведению ее крайних членов. 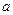
Рассмотрим пример:
Определите процентную концентрацию раствора 2:5000.
Пример: В отделении за сутки в среднем расходуется 0,5кг хлорной извести. Во время генеральной уборки помещений было израсходовано 153% среднесуточного количества хлорной извести. Сколько хлорной извести израсходовал персонал отделения во время генеральной уборки помещения?
Пропорция: 0,5:х = 100:153
Х = 0,5·153:100 = 0,765 (г)
Пример:
За сутки отделение израсходовало 765г хлорной извести вместо среднесуточной нормы расхода 500г. На сколько процентов больше израсходовано хлорной извести?
Пропорция: 500:765 = 100:х Х = 765·100:500 = 153%
153 – 100 = 53% (больше израсходовали вещества).
В медицине используют 3 основные метрические единицы.
1.МЕТР (м) – мера длины.
| Производная единица | Значение |
| Дециметр (дм) | 0,1м |
| Сантиметр (см) | 0,01м |
| Миллиметр (мм) | 0,001м |
| Микрометр (мкм) | 0,000001м |
2.ГРАММ (г) – мера массы
| Производная единица | Значение |
| Микрограмм (мкг) | 0,000001г |
| Миллиграмм (мг) | 0,001г |
| Сантиграмм (сг) | 0,01г |
| Дециграмм (дг) | 0,1г |
| Декаграмм (даг) | 10г |
| Гектограмм (гг) | 100г |
| Килограмм (кг) | 1000г |
3. ЛИТР (л) – мера объема.
| Производная единица | Значение |
| Децилитр (дл) | 0,1л |
| Сантилитр (сл) | 0,01л |
| Миллилитр (мл) | 0,001л |
| Микролитр (мкл) | 0,000001л |
| Декалитр (дал) | 10л |
| Гектолитр (гл) | 100л |
| Килолитр (кл) | 1000л |
Формула расчета количества таблеток и капсул, объема лекарственных средств для применения внутрь в жидком виде.
ТАБЛЕТКИ И КАПСУЛЫ
Формула расчета количества таблеток и капсул, объема лекарственных средств для применения внутрь в жидком виде.
Давая больному таблетки и капсулы, лекарственные средства в жидком виде, нужно помнить следующее правило:
дозировка препарата, имеющегося у вас, и дозировка, назначенная врачом, должны быть в одинаковых единицах.
Для пересчета дозы препарата можно использовать следующую формулу:
Требуемая доза – доза, назначенная врачом.
Доза имеющегося препарата – количество препарата в одной таблетке (выраженное в г, мг и т.д.).
Требуемое количество препарата – всегда Х (сколько таблеток вы должны дать больному).
Количество имеющегося препарата – объем (обычно в мл).
Так, если врач назначил 1г препарата, а у медсестры имеются таблетки препарата по 500мг, то она должна знать, что 1г=1000мг, и таким образом дать больному 1000/500=2 таблетки.
Жидкую форму лекарственных средств можно использовать в тех случаях, когда больной не может глотать таблетки.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
СПОСОБЫ ВЫРАЖЕНИЯ КОНЦЕНТРАЦИИ РАСТВОРА: ПРОЦЕНТНАЯ КОНЦЕНТРАЦИЯ (ИЛИ МАССОВАЯ ДОЛЯ РАСТВОРЕННОГО ВЕЩЕСТВА)
Формула концентрации раствора. Их множество. И каждая соответствует тому или иному способу выражения концентрации. А в химии их применяются достаточно: массовая доля растворенного вещества, молярная, нормальная, моляльная, титр и др.
А зачем так много? Ответ на этот вопрос очень прост. Каждый вид концентрации удобен в том или ином конкретном случае, тогда как применение другого вида концентрации неуместно.
Например, при исследовании содержания массы вещества в очень небольшом объеме раствора удобно пользоваться титром. А в каких-то технологиях вообще концентрация заменяется другими количественными характеристиками раствора. Так, в технологии посола рыбы для расчета необходимой концентрации тузлука (раствора поваренной соли) используют не его процентную концентрацию, а плотность.
Концентрация – что это такое
Любой раствор имеет различные характеристики: качественные и количественные. Одной из важнейших количественных характеристик является концентрация раствора.
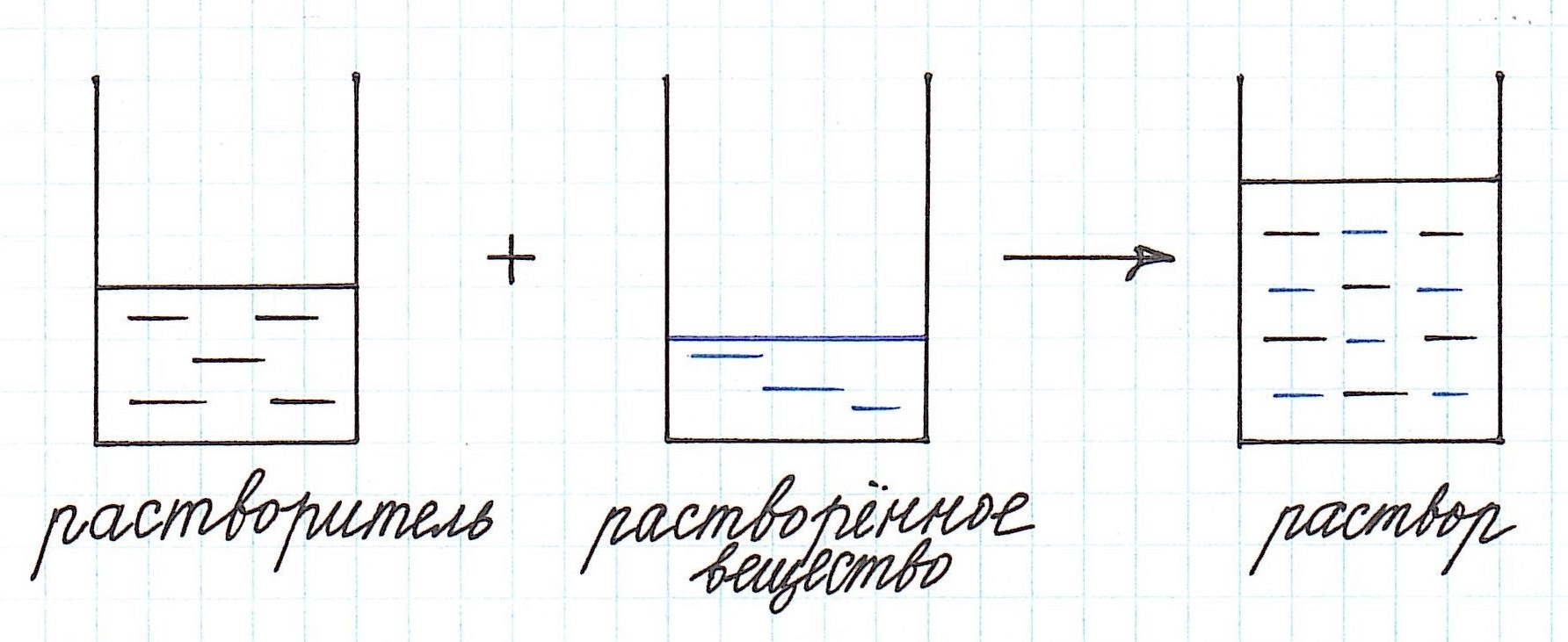
Концентрация раствора – это количество растворенного вещества, содержащееся в определенном количестве раствора.
Как видно из приведенного определения, основными компонентами раствора являются:
Растворенного вещества в растворе всегда меньше, а растворителя больше.
И вот именно с вычислением количественного содержания растворенного вещества чаще всего и связаны все расчеты, основанные на применении формулы концентрации раствора.
Существует несколько видов концентрации раствора:
— массовая доля растворенного вещества;
— объемная доля растворенного вещества;
— молярная доля растворенного вещества;
— молярная (или молярность);
— моляльная (или моляльность);
— нормальная (или эквивалентная);
Формула концентрации раствора: основные виды
Применение того или иного вида концентрации уместно в каждом конкретном случае. Не существует какой-то универсальной концентрации или универсальной формулы концентрации раствора.
Кстати, с помощью математических преобразований можно перейти от одной концентрации к другой или найти взаимосвязь между разными их видами.
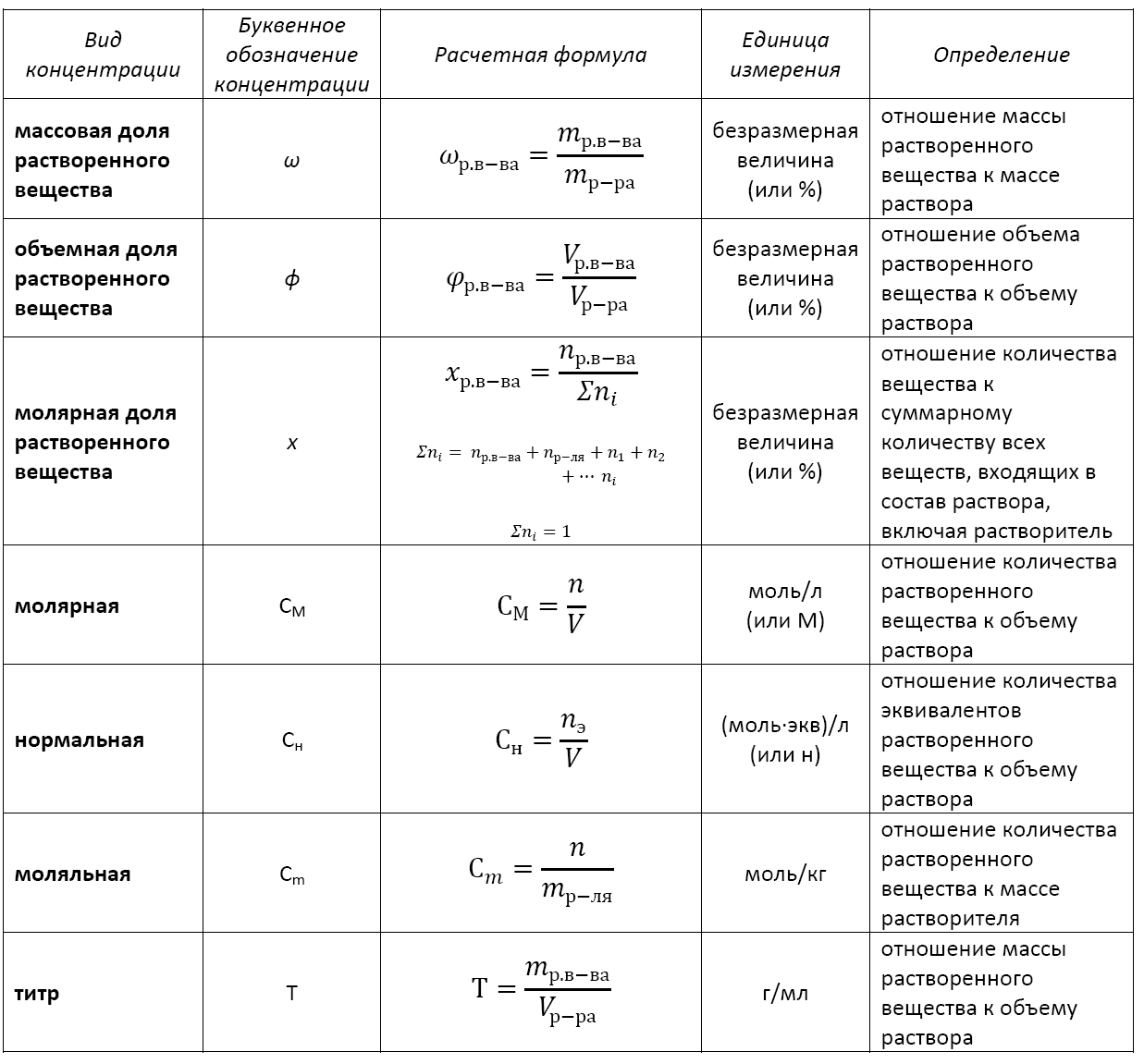
Основные расчетные формулы концентрации раствора приведены в таблице:
Массовая доля растворенного вещества и примеры ее вычисления
Массовая доля растворенного вещества – это отношение массы растворенного вещества к массе раствора.
Ее расчетная формула выглядит так:
где ωр.в-ва – массовая доля растворенного вещества, mр.в-ва – масса растворенного вещества, mр-ра – масса раствора.
ωр.в-ва представляет собой долю или от единицы или от 100%. Так, например, имеется двухпроцентный раствор NaCl. Его концентрация будет записана в первом случае ω(NaCl) = 0,02, а во втором – ω(NaCl) = 2%. Форма записи основной сути не меняет. Можно записывать и так, и так.
Что же означает выражение ω(NaCl) = 0,02 или ω(NaCl) = 2%? Буквально следующее: в 100 г водного раствора поваренной соли содержится 2 г этой соли и 98 г воды.
Тогда основную расчетную формулу для массовой доли растворенного вещества можно преобразовать:
Очень часто в расчетах с процентной концентрацией используются плотность и объем раствора:
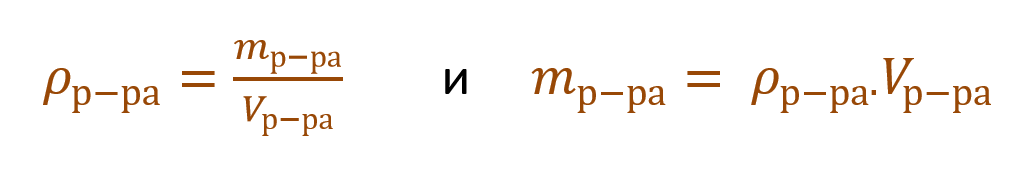
В других ситуациях могут использоваться объем и плотность не раствора, а растворителя. Тогда основная формула для расчета концентрации будет выглядеть так:
На практике бывает необходимо не только приготовить раствор с какой-либо определенной концентрацией, но и увеличить, либо уменьшить ее значение. Это достигается различными приемами:
— добавлением растворенного вещества;
— добавлением к раствору растворителя (например, воды).
Кроме того, приходится часто смешивать друг с другом растворы разных концентраций.
Разберем все возможные случаи.
Мы рекомендуем задачи, в которых речь идет о растворах, решать с использованием схематических рисунков. Это очень наглядно, особенно, когда речь идет о смешивании растворов.
Начнем с самого простого: вычислим концентрацию раствора.
Пример 1. В 200 г воды растворили 40 г глюкозы. Вычислите массовую долю глюкозы в полученном растворе.
Обратите внимание, что речи о каком-либо химическом взаимодействии не идет! Поэтому записывать уравнения реакций не требуется!
Запишем общую формулу для расчета массовой доли растворенного вещества:
В данной задаче глюкоза (C6H12O6) – растворенное вещество, а вода (H2O) – растворитель. Масса раствора будет складываться из массы глюкозы и массы воды:
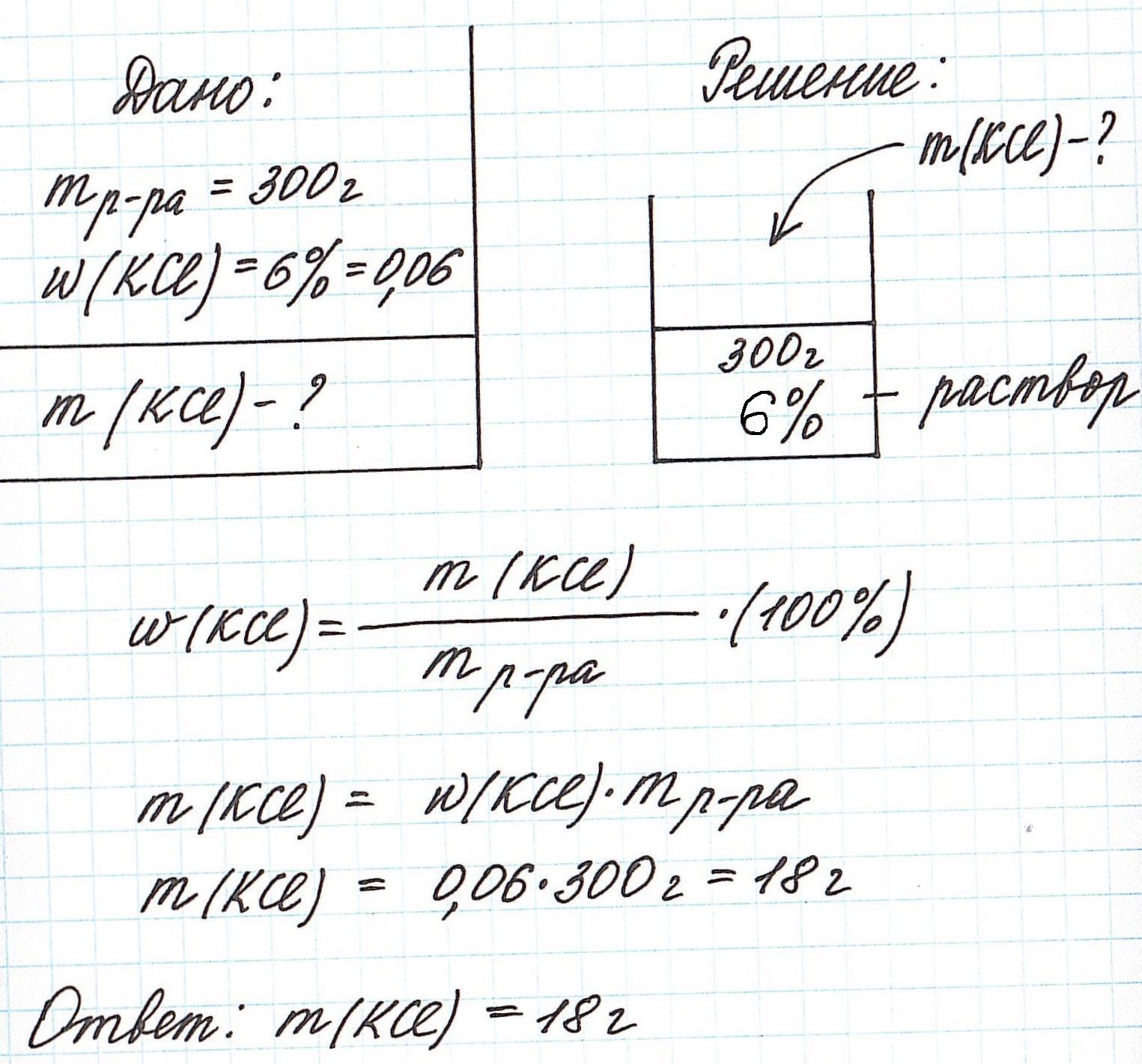
Пример 2. Рассчитайте, сколько потребуется хлорида калия, чтобы приготовить 300 г раствора с массовой долей соли 6%.
Обратите внимание, для того, чтобы расчеты были менее громоздкими, будем использовать выражение концентрации не в %, а в долях от единицы.
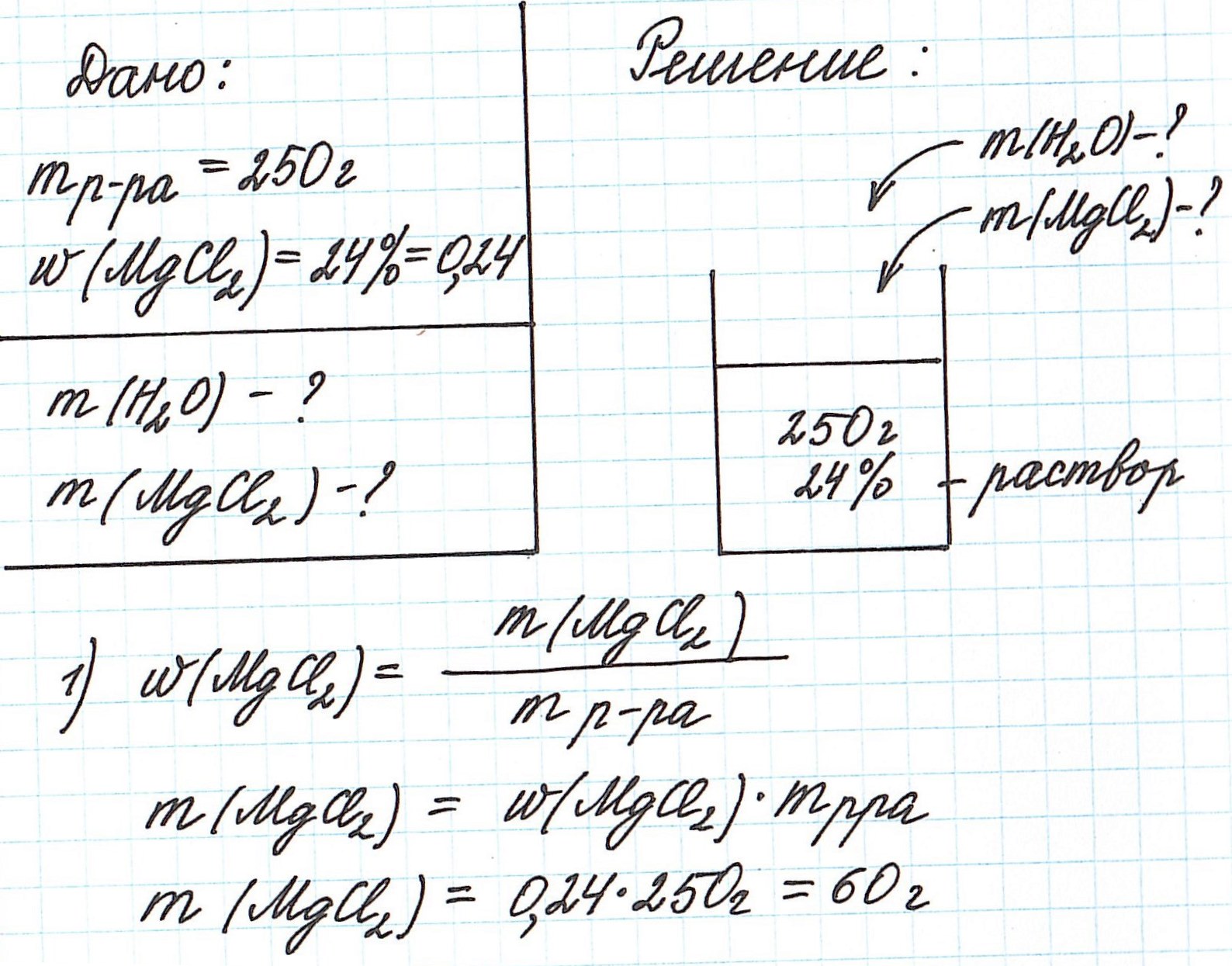
Пример 3. Необходимо приготовить 250 г раствора с массовой долей хлорида магния 24%. Рассчитайте массу требуемых воды и соли.
Так как раствор готовится из хлорида магния и воды, то и масса раствора равна сумме масс хлорида магния и воды:
Рассмотрим задачу, в которой в качестве растворителя выступает не вода, а другое вещество.
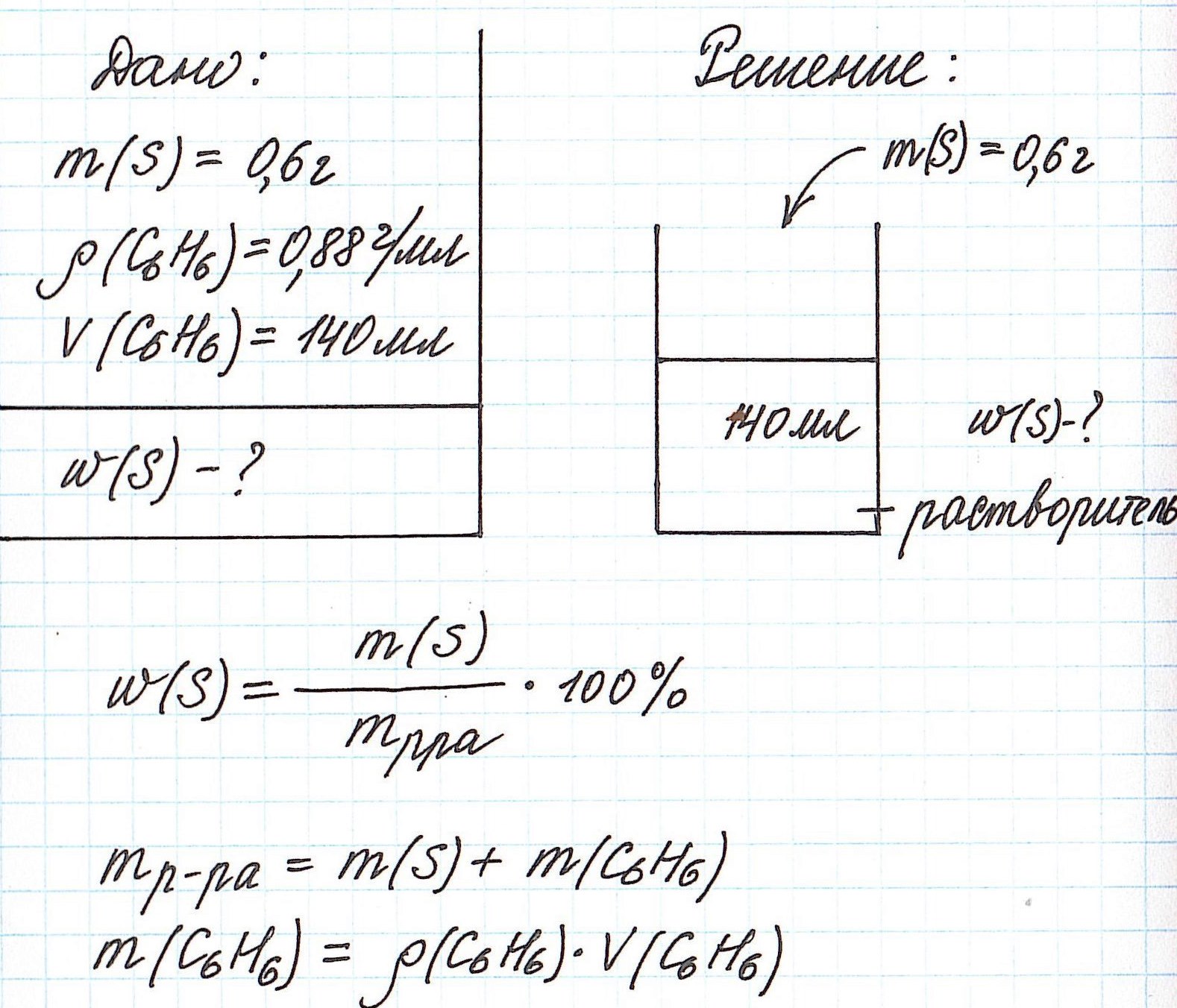
Пример 4. В органическом растворителе бензоле объемом 140 мл растворили серу массой 0,6 г. Вычислите массовую долю серы в полученном растворе, если плотность бензола составляет 0,88 г/мл.
Обратите внимание, что здесь:
— масса раствора не известна;
— масса растворителя (бензола) не известна;
— известны объем и плотность растворителя (бензола), что позволяет нам найти его массу;
— масса раствора состоит из массы растворителя (бензол) и массы растворенного вещества (сера).
Объединим все расчетные формулы в одну и подставим в нее имеющиеся численные значения:
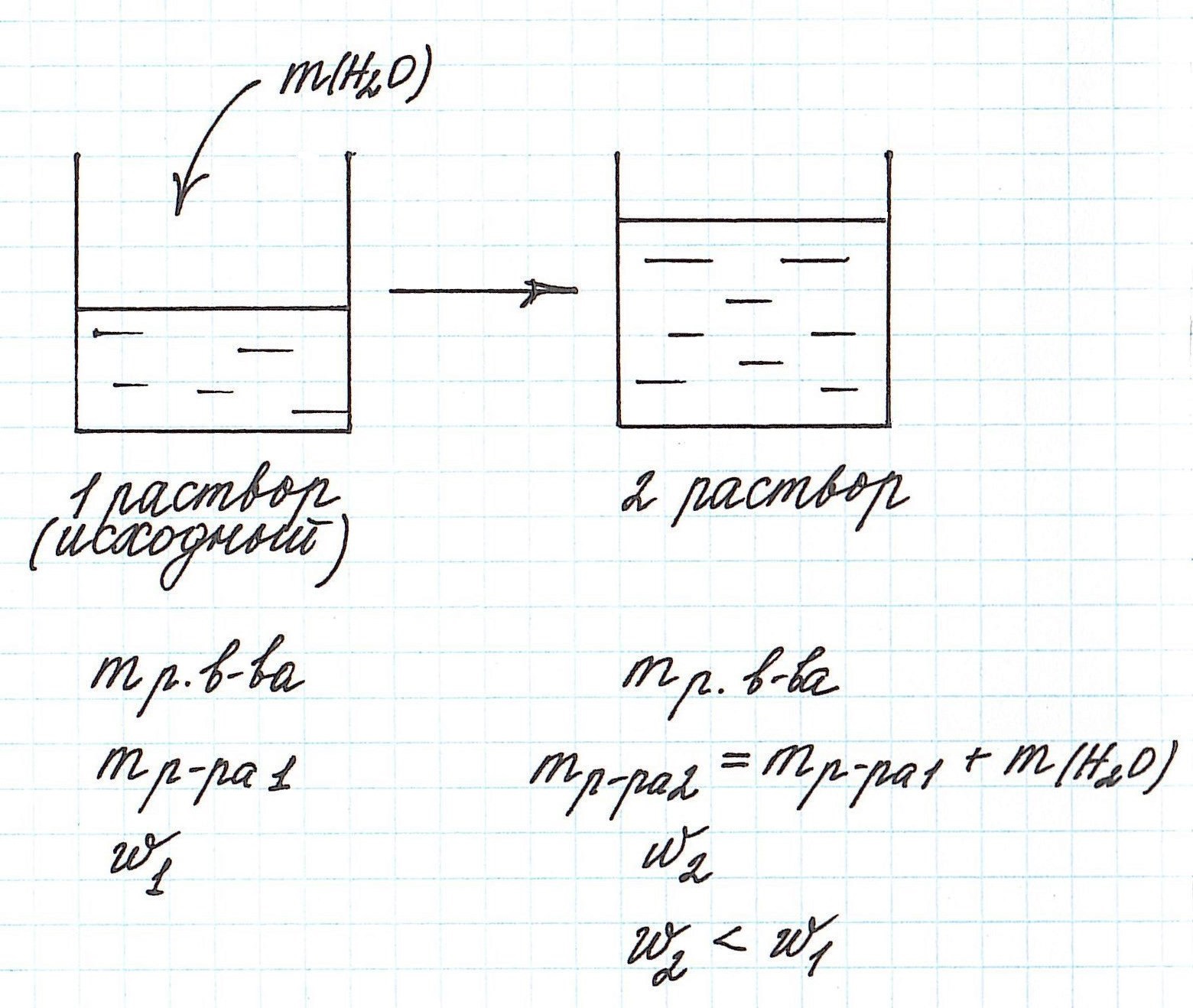
Вычисление массовой доли растворенного вещества при разбавлении раствора водой
Разбавление раствора водой приводит к уменьшению его концентрации.
Запомним, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворителя;
— масса растворенного вещества остается постоянной.
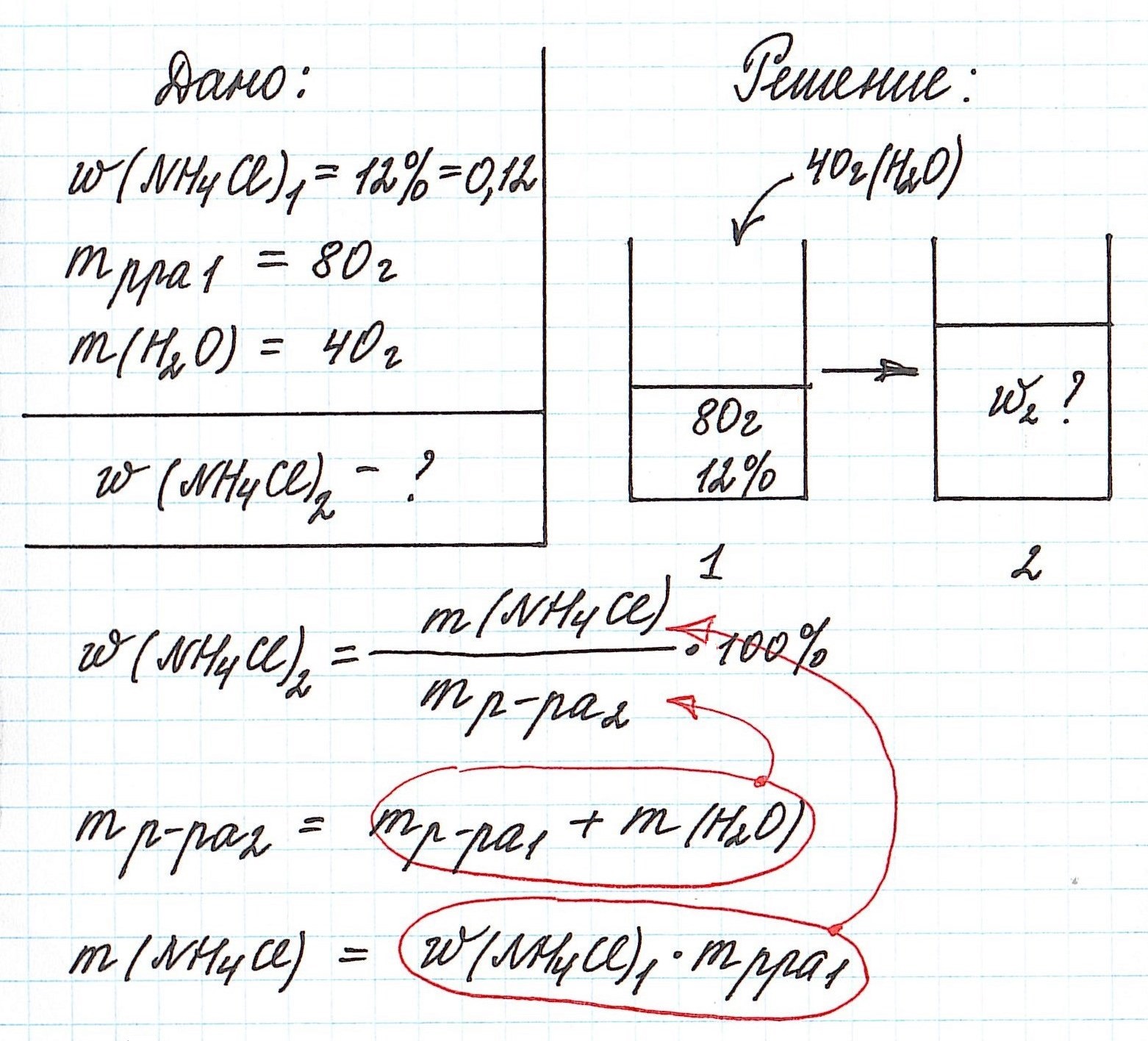
Пример 5. К 80 г раствора с массовой долей NH4Cl 12% добавили 40 г воды. Вычислите массовую долю хлорида аммония в полученном растворе.
Объединим все полученные формулы в одну и подставим имеющиеся данные:
Пример 6. Рассчитайте объем раствора фосфорной кислоты (массовая доля кислоты 12%, плотность 1,065 г/мл), который потребуется для приготовления раствора с массовой долей H3РO4 4% объемом 250 мл (плотность 1,02 г/мл).
В данной задаче речь напрямую о разбавлении раствора не идет. Но судя по тому, что исходный раствор имел концентрацию 12%, а конечный – 4%, становится ясно: последний раствор можно получить путем разбавления первого водой.
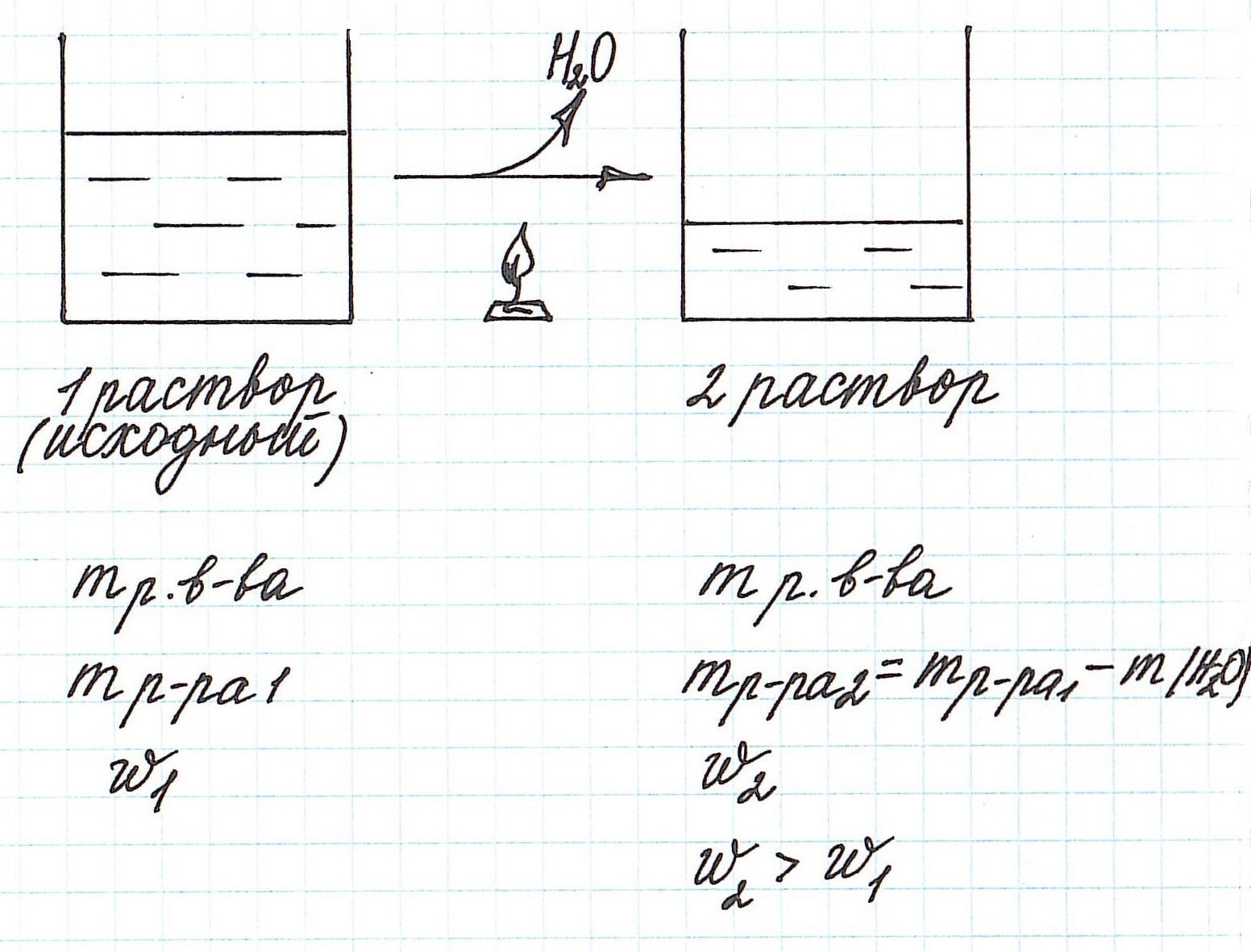
Вычисление массовой доли растворенного вещества при концентрировании раствора путем упаривания
Упаривание раствора, т.е. его нагревание, при котором происходит испарение воды, приводит к увеличению концентрации.
Учтите, что при этом:
— уменьшается масса раствора;
— уменьшается масса растворителя;
— масса растворенного вещества остается постоянной (при условии, что растворенное вещество не разлагается при данной температуре).
Пример 7. Из 200 г 27%-ного раствора глюкозы выпарили 20 г воды. Определите массовую долю глюкозы в полученном растворе.
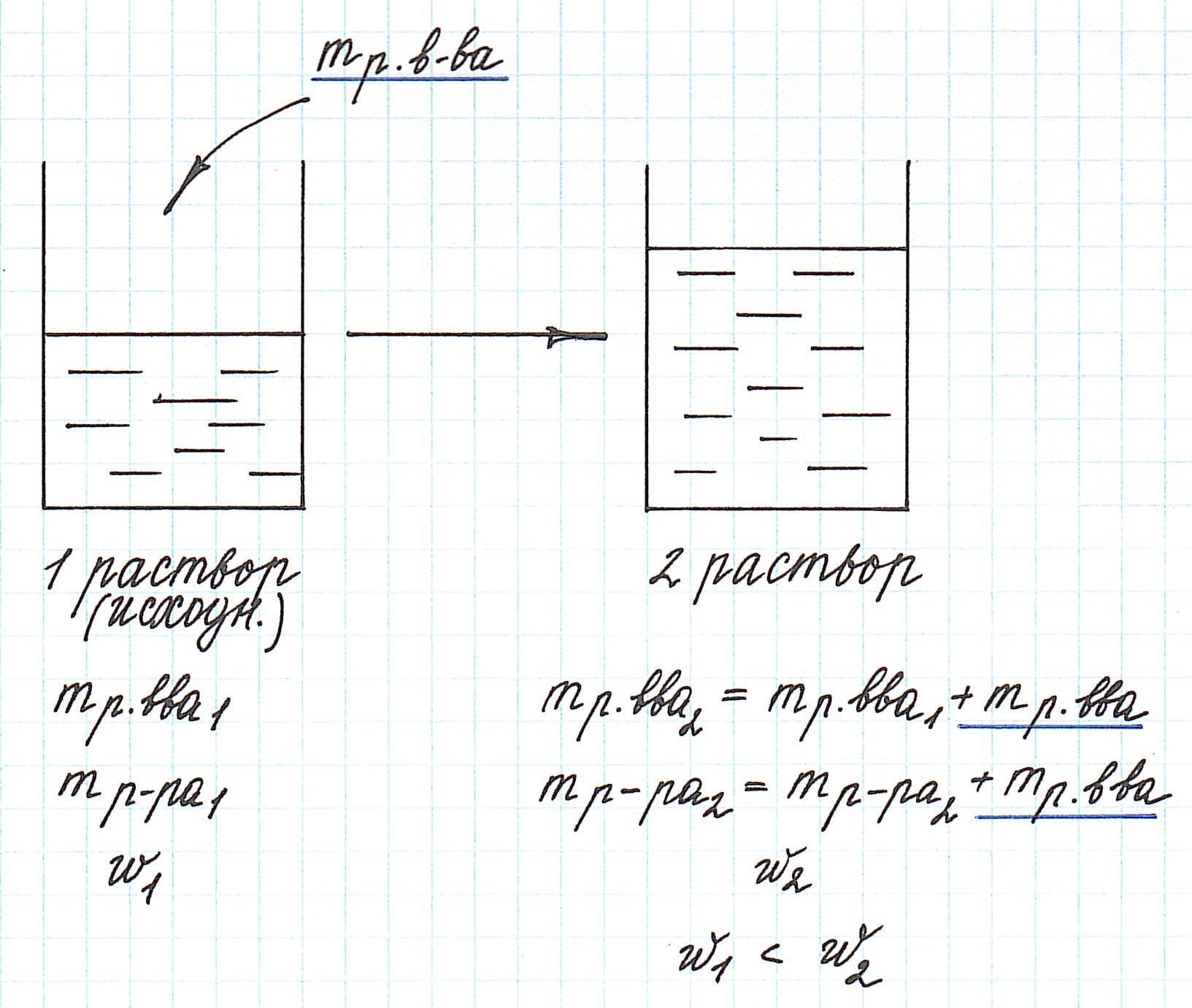
Вычисление массовой доли растворенного вещества при концентрировании раствора путем добавления растворенного вещества
Добавление к уже существующему раствору новой порции растворенного вещества приводит к увеличению концентрации раствора.
Помните, что в таких случаях:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества.
Пример 8. Определите массу хлорида калия, который надо добавить к 180 г 15%-ного раствора этой соли, чтобы получить 20%-ный раствор.
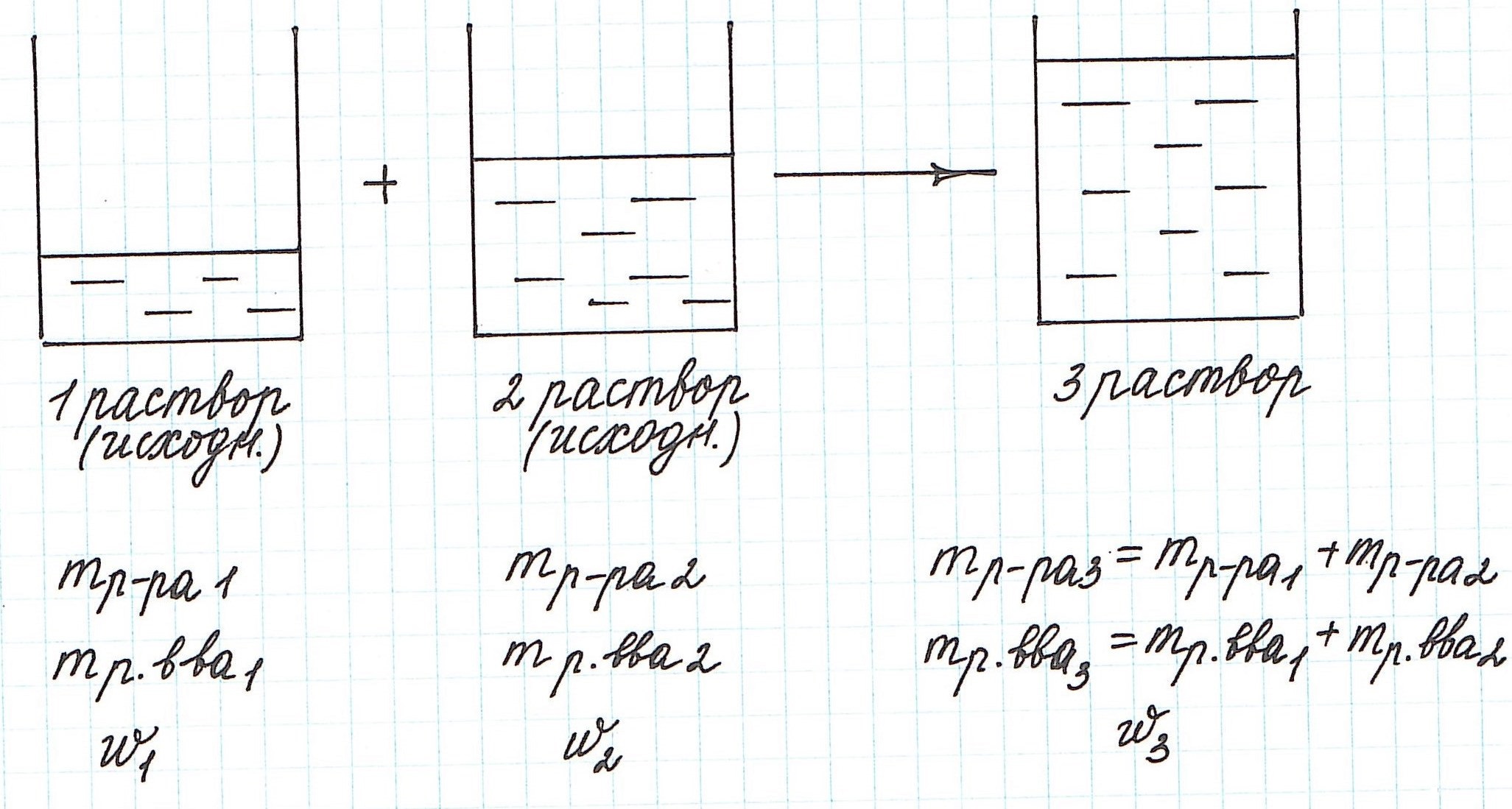
Вычисление массовой доли растворенного вещества при смешивании двух растворов
При смешивании двух растворов (речь о растворах одного и того же вещества конечно же) изменяются все количественные характеристики:
— увеличивается масса раствора;
— увеличивается масса растворенного вещества;
— изменяется массовая доля растворенного вещества.
Пример 9. Смешали 80 г 32%-ного раствора и 30 г 10%-ного раствора нитрата меди (II). Какова концентрация соли в полученном растворе?
Вычисление массовой доли растворенного вещества с применением кристаллогидратов для приготовления раствора
Кристаллогидраты используются для приготовления растворов довольно часто. Кристаллогидраты представляют собой вещества, в состав которых помимо основного вещества входят молекулы воды. Например:
CuSO4·5H2O – кристаллогидрат сульфата меди (II) (или медный купорос);
Na2SO4·10H2O – кристаллогидрат сульфата натрия (или глауберова соль).
Кристаллогидраты различаются прочностью связи между основным веществом и кристаллизационной водой. Одни из них теряют воду при комнатной температуре с течением времени и перестают быть кристаллогидратами (например, Na2СO3·10H2O). Другие – обезвоживаются только при сильном нагревании (например, CuSO4·5H2O).
При расчете концентрации с использованием кристаллогидратов для получения растворов часто приходится учитывать и кристаллизационную воду.
Но сначала поясним некоторые нюансы на конкретном примере:
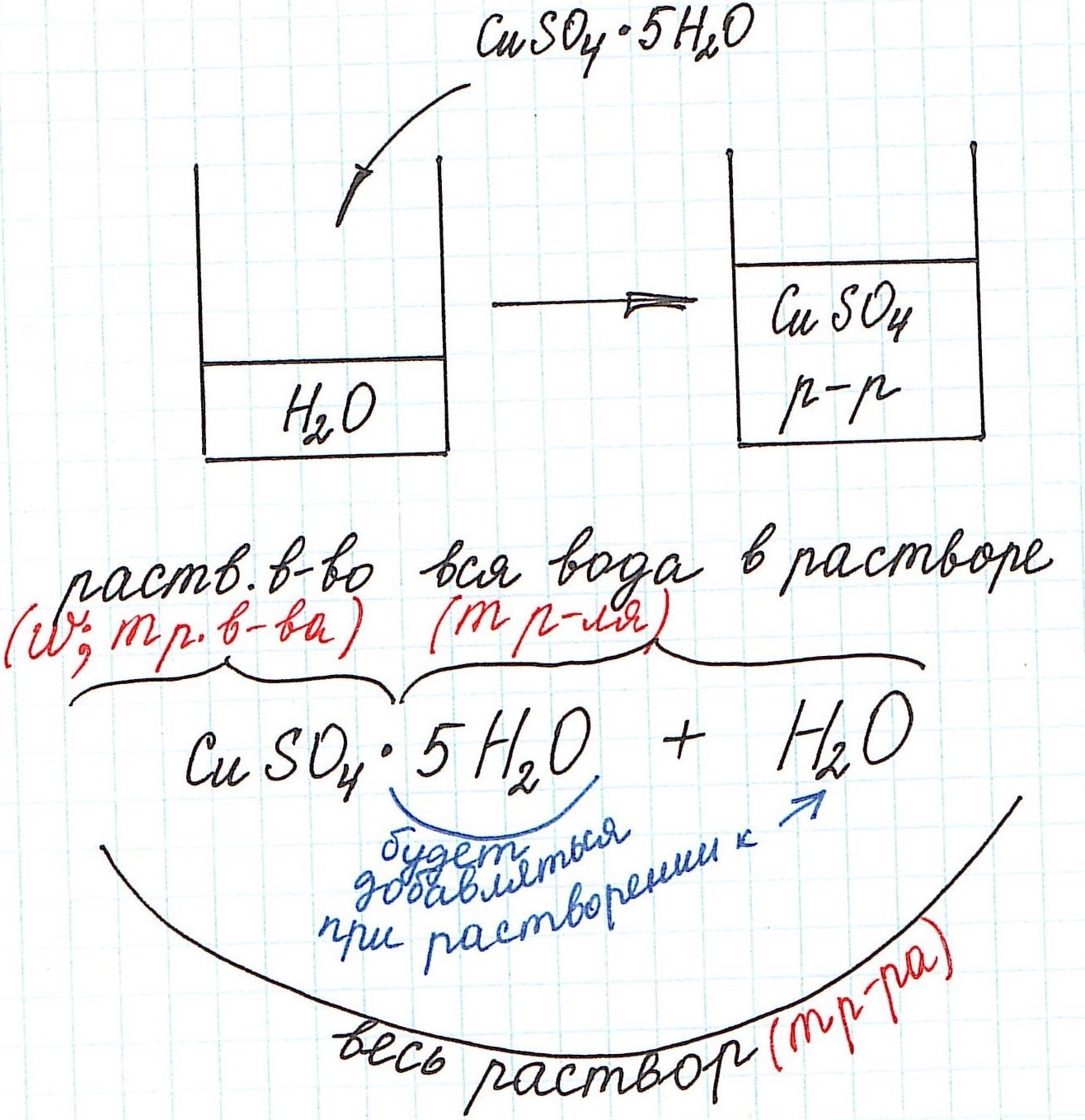
1) Формула CuSO4·5H2O означает, что 1 моль CuSO4·5H2O содержит 1 моль CuSO4 и 5 моль H2O. Это можно было бы записать так:
2) Относительная молекулярная (и численно молярная) масса будет складываться из относительной молекулярной массы вещества и относительной молекулярной массы воды. Например:
Mr(CuSO4·5H2O) = Mr(CuSO4) + 5·Mr(H2O) = 160 + 5·18 = 250 и, соответственно,
3) Еще одну особенность поясним с помощью рисунка:
Итак, разберем несколько типичных задач.
Пример 10. В 60 г воды растворили глауберову соль Na2SO4·10H2O массой 5,6 г. Какова массовая доля сульфата натрия в полученном растворе?
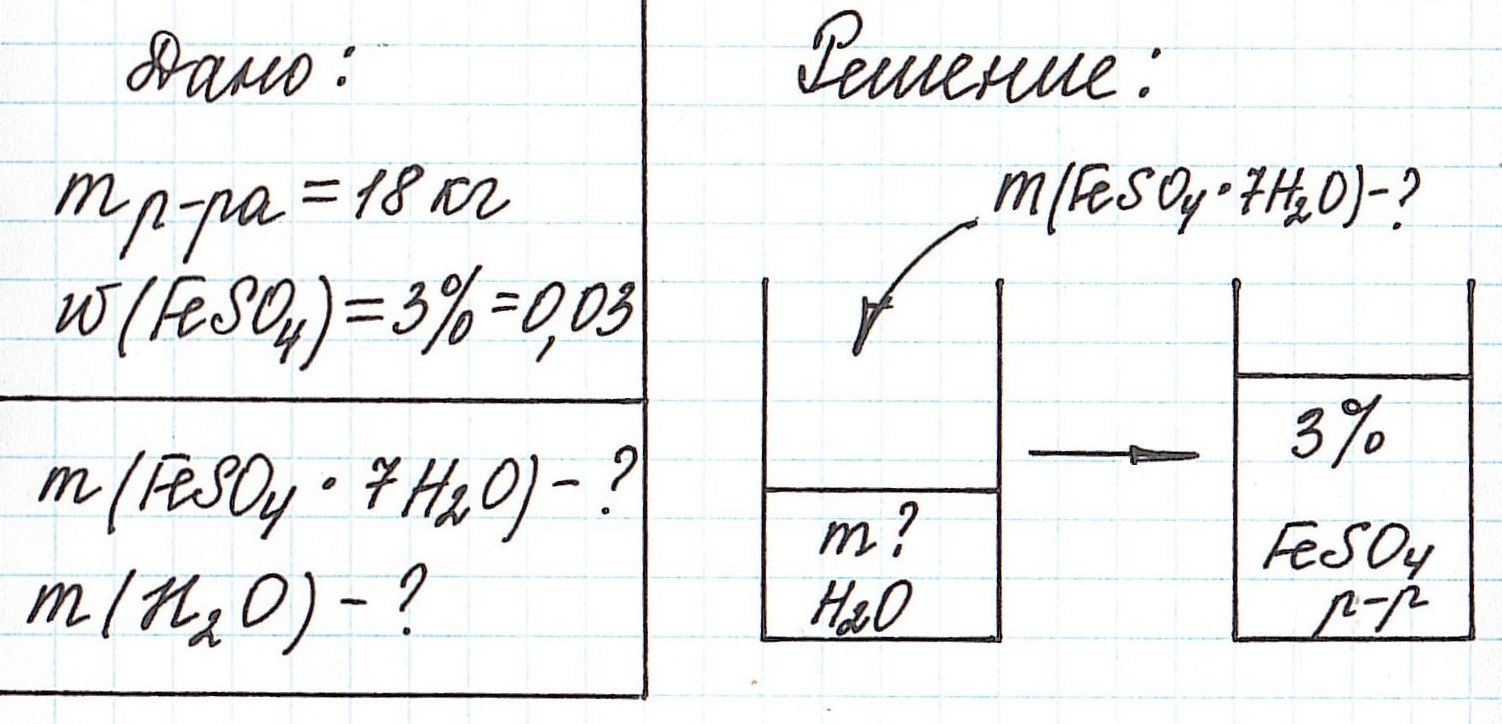
Пример 11. Какая масса железного купороса FeSO4·7H2O и воды потребуется для приготовления 18 кг раствора сульфата железа (II) с массовой долей FeSO4 3%?
Обратите внимание, что масса раствора дана не в граммах (г), а в килограммах (кг). Для того, чтобы привести в ходе расчетов все единицы измерения к единой системе, можно перевести килограммы в граммы и вычислять как обычно.
Но есть более простой способ. Можно считать количество вещества не в моль, а в киломоль (кмоль). Молярную массу вычислять не в г/моль, а в кг/кмоль. В этом случае ответ в задаче мы сразу получим в килограммах.
Пример 12. Вычислите массу кристаллогидрата сульфата никеля NiSO4·7H2O, который надо добавить к 180 г раствора с массовой долей сульфата никеля 1,5%, чтобы получить раствор с массовой долей соли 6%?
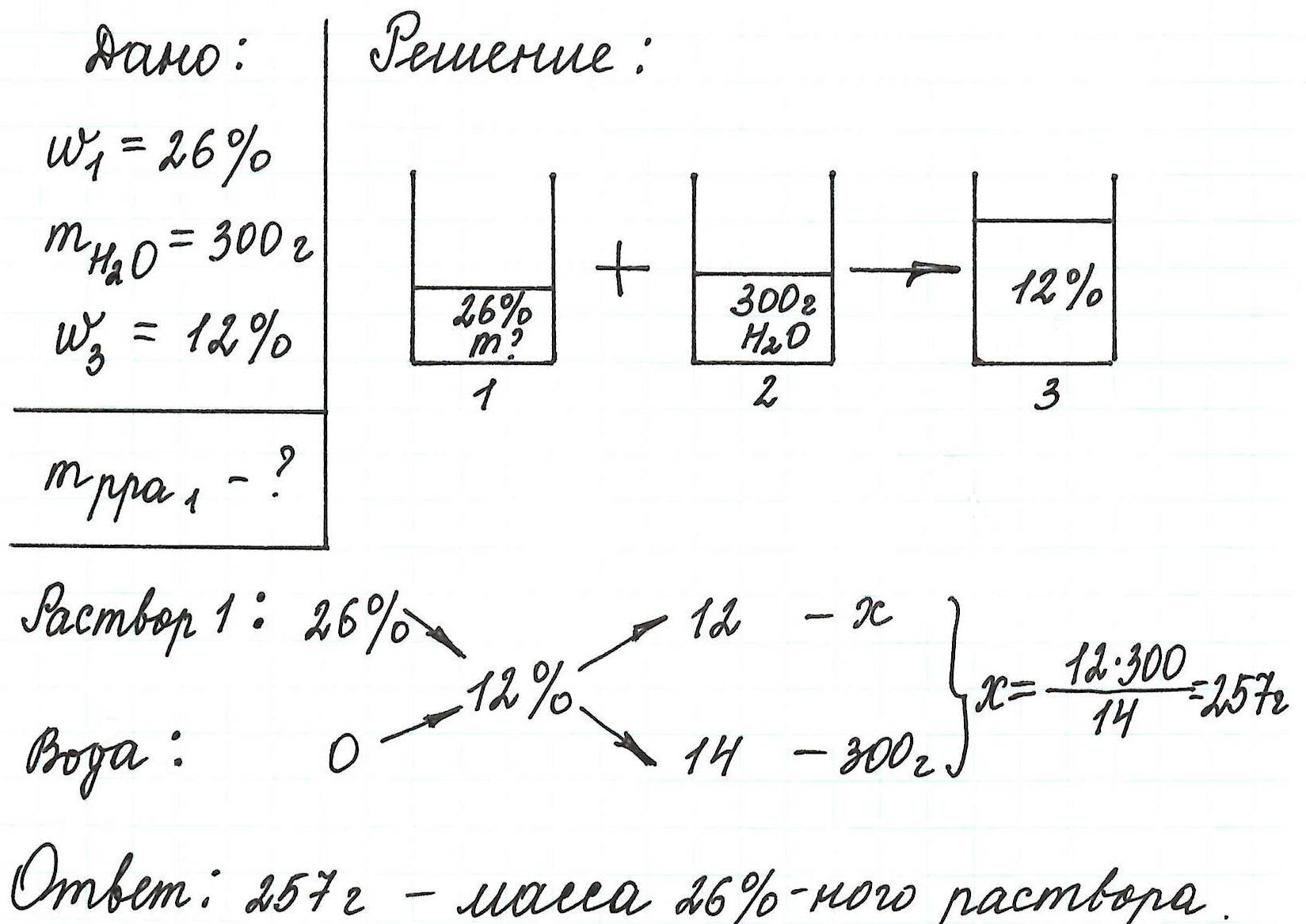
Правило «креста» в химии растворов как метод решения задач на процентную концентрацию растворов
Правилом «креста» (или «квадратом Пирсона») очень удобно пользоваться в расчетах, связанных с разбавлением или смешиванием растворов.
Общая схема вычислений выглядит так:
Пример 13. Какую массу 5%-ного раствора глюкозы надо добавить к 70 г 21%-ного раствора этого же вещества, чтобы получить 12%-ный раствор?
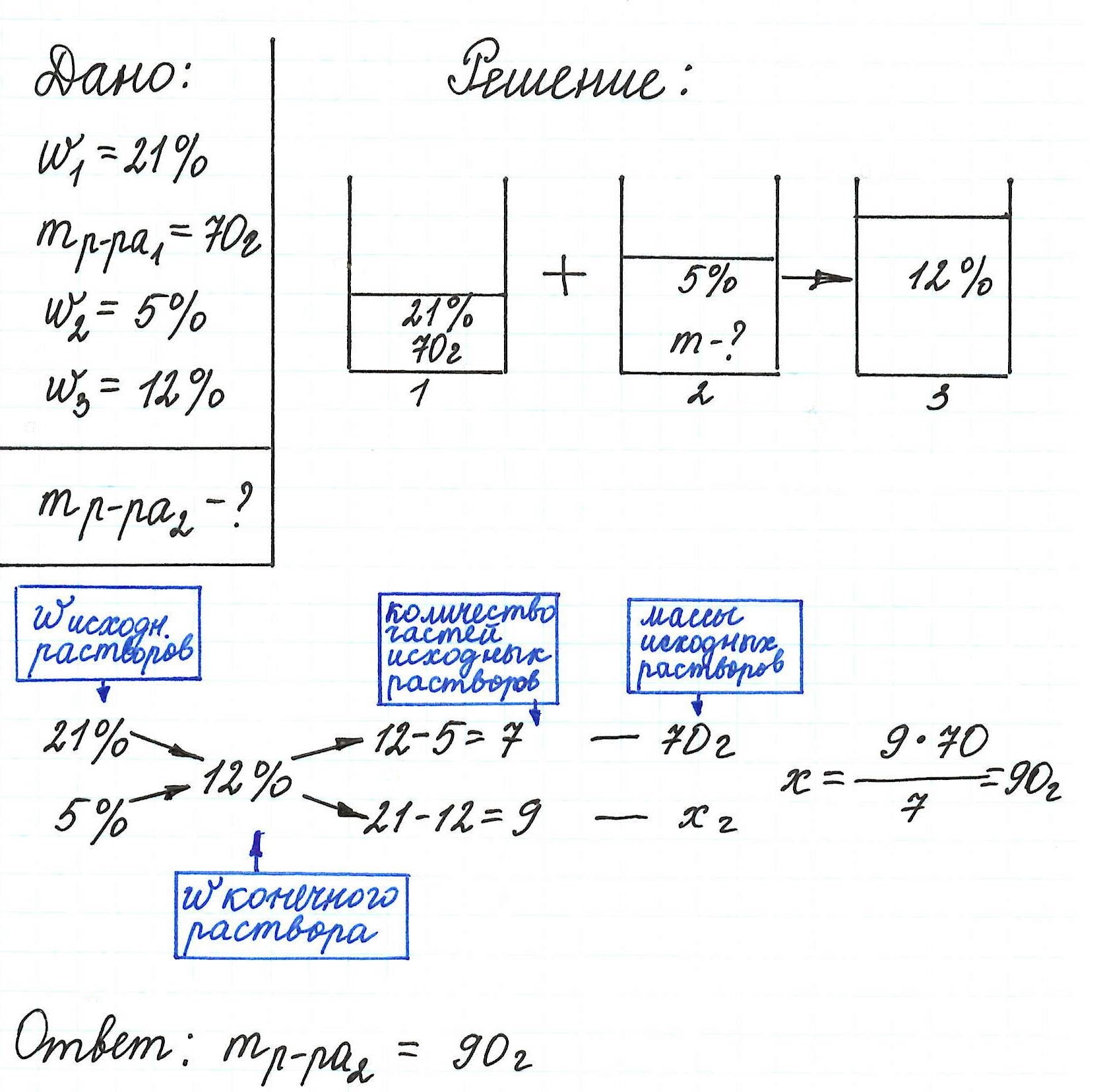
Еще примеры с применением правила «креста» можно посмотреть здесь.
Мы рассмотрели достаточно примеров расчетов, где используется формула такой концентрации раствора как массовая доля растворенного вещества. Как видим, ситуаций, в которых требуется ее применение, множество. Однако, есть достаточно случаев, когда более приемлемыми являются формулы других концентраций (молярной, нормальной, титра и т.д.). Об этом читайте в других статьях.