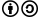как узнать радиус по длине и высоте
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Как найти радиус окружности
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как узнать радиус по длине и высоте

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент 
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте 
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Длина окружности через хорду и высоту
ремонт своими руками
Сегмент — плоская фигура, заключённая между дугой и её хордой. Как частный случай, круговой сегмент: часть круга, ограниченная дугой окружности и её хордой или секущей.
Для начала расчёта выберите известные параметры, по которым будут произведены расчёты, за тем введите их и нажмите кнопку «Рассчитать».
Если Вам необходим узнать по каким формулам ведется расчет для фигуры, а так же задать единицы измерения или сохранить расчет в PDF, то воспользуйтесь сайтом calc-online24.ru
Программа предназначена для вычисления высоты сегмента круга (окружности) при известных радиусе и хорде.
Сегментом можно назвать часть круга, лежащую между хордой данной окружности и дугой этой же окружности.
Формула для вычисления высоты сегмента круга (окружности) при известных радиусе и хорде имеет следующий вид:
Чтобы найти высоту сегмента круга (окружности), введите значения радиуса и хорды, и нажмите кнопку «ВЫЧИСЛИТЬ».
Программа определит высоту сегмента круга h.
Исходные данные и результат вычислений можно копировать в буфер обмена для дальнейшего использования в других программах.
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Как определить радиус окружности, зная ее длину
Содержание статьи
«Учат в школе, учат в школе…»
По учебной программе шестого класса учащиеся общеобразовательных школ в курсе геометрии изучают круг и окружность как геометрическую фигуру, и все, что с этой фигурой связано. Ребята знакомятся с такими понятиями, как радиус и диаметр, длина окружности или периметр круга, площадь круга. Именно на этой теме они узнают про загадочное число Пи – это лудольфово число, как оно называлось раньше. Число Пи иррационально, так как его представление в виде десятичной дроби бесконечно. На практике используется его усеченный вариант из трех цифр: 3.14. Эта константа выражает отношение длины любой окружности к ее диаметру.
Шестиклассники решают задачи, выводя по одной данности и числа «Пи» остальные характеристики окружности и круга. В тетрадях и на классной доске они в масштабе вычерчивают абстрактные сферы и производят мало что говорящие вычисления.
А на практике
На практике такая задача может возникнуть в ситуации, когда, например, возникает необходимость проложить трассу определенной протяженности для проведения каких-либо состязаний со стартом и финишем в одном месте. Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона. Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.
Радиус из окружности
Итак, предположим, что вам для проведения соревнований по автокроссу необходима круговая трасса длиной 10 000 м. Вот нужная формула для определения радиуса (R) окружности при известной её длине (C):
R=C/2п (п – число, равное 3.14).
Подставив имеющиеся значения, вы легко получаете результат:
R = 10 000:3.14 = 3 184. 71 (м) или 3 км 184 м и 71 см.
От радиуса к площади
Зная радиус окружности, легко можно определить площадь, которая будет изъята из ландшафта. Формула площади круга (S): S=пR2
При R = 3 184. 71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.
Подобные вычисления могут быть полезными при огораживании. Например, у вас имеется материал на ограду на столько-то погонных метров. Взяв эту величину за периметр круга, вы легко определите его диаметр (радиус) и площадь, а, следовательно, зримо представите величину будущего огороженного участка.