как узнать радиус скругления
Простая формула для определения радиуса дуги
Полезно знать математический способ, позволяющий рассчитать радиус дуги. Он особенно удобен, когда требуется точно разметить плавную дугу с помощью большого импровизированного циркуля, а не гибкого лекала, после того как вам стали известны три опорные точки или два главных размера.

Например, если нужно построить дугу длиной 240 и высотой 30 мм, следует действовать так:
Сначала подставьте эти размеры в формулу. В нашем случае L=120, Н=30, поэтому (1202+302): (2×30) = (14400+900): 60= 153000:60 = 255.
Теперь сделайте для этого радиуса циркуль, как показано на фото внизу. Выровняйте один конец с серединой дуги на заготовке. Проведите из этой точки под прямым углом по линейке прямую линию и поставьте на нее второй конец циркуля. Теперь вы можете начертить идеальную дугу, которая соединит все три опорные точки.
September 12, 2013
При создании макетов в Photoshop дизайнеры очень любят использовать скругление углов для самых различных блоков.
Причем, они любили это делать всегда, с самых незапамятных времен. Спору нет, блоки с такими углами смотрятся гораздо приятнее, что положительным образом сказывается на самом дизайне сайта.
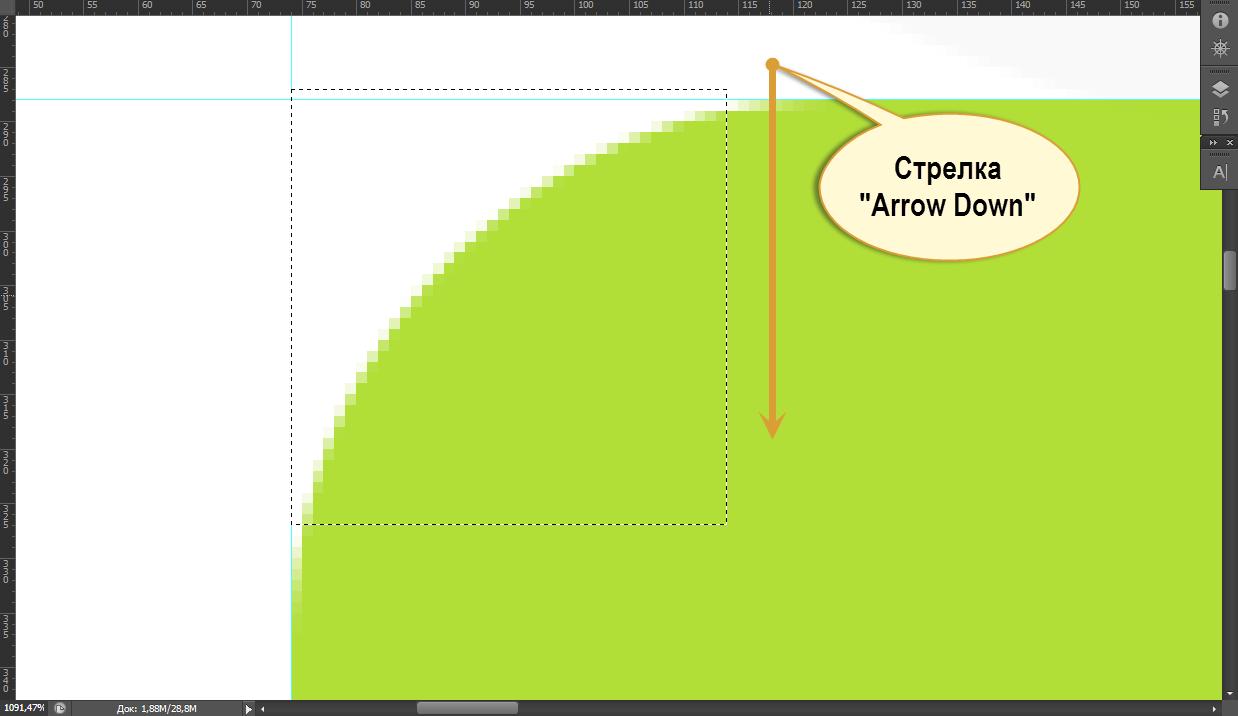
Но речь в данной статье не об этом. Точнее, не о том, как создать скругленный угол в CSS3. А о том, как померить этот угол на psd-макете. Допустим, у нас есть присланный дизайнером макет сайта:
Скажу, что сразу ответ на этот вопрос я не получил. По привычке отправился на форум forum.htmlbook.ru, но конкретного ничего не вынес оттуда. После поисков в Инете все-же решение было найдено. И оно оказалось очень простым.
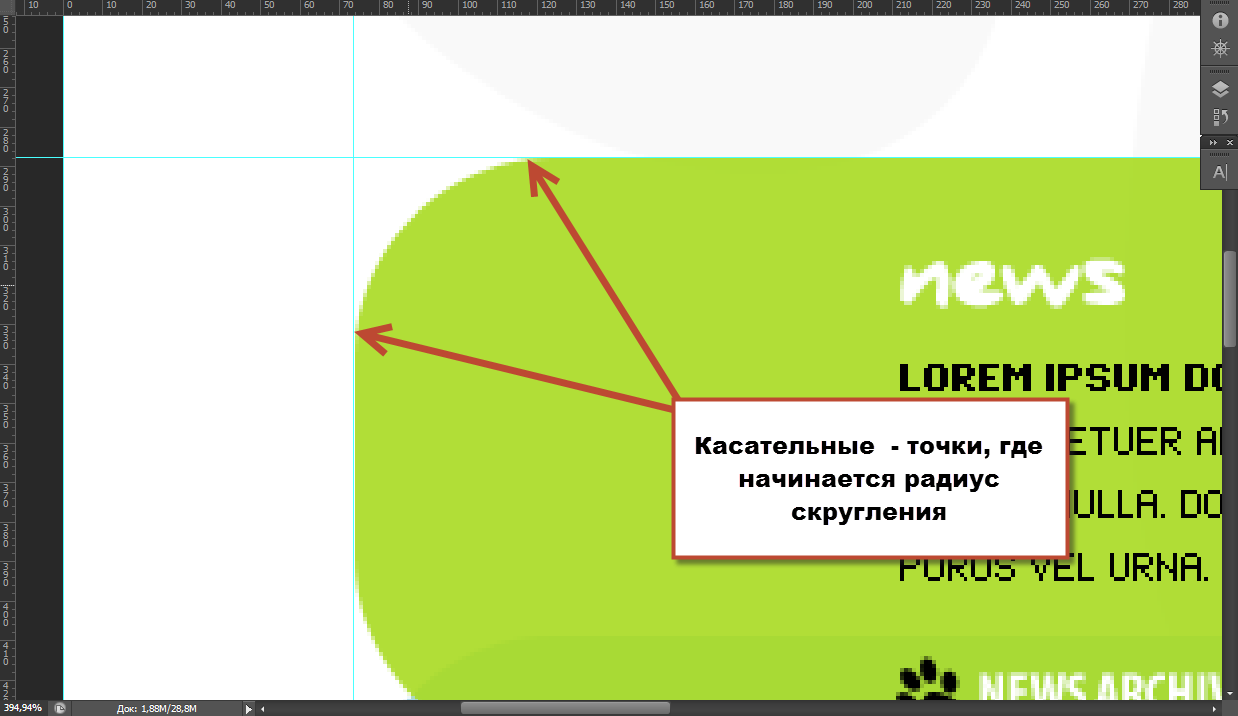
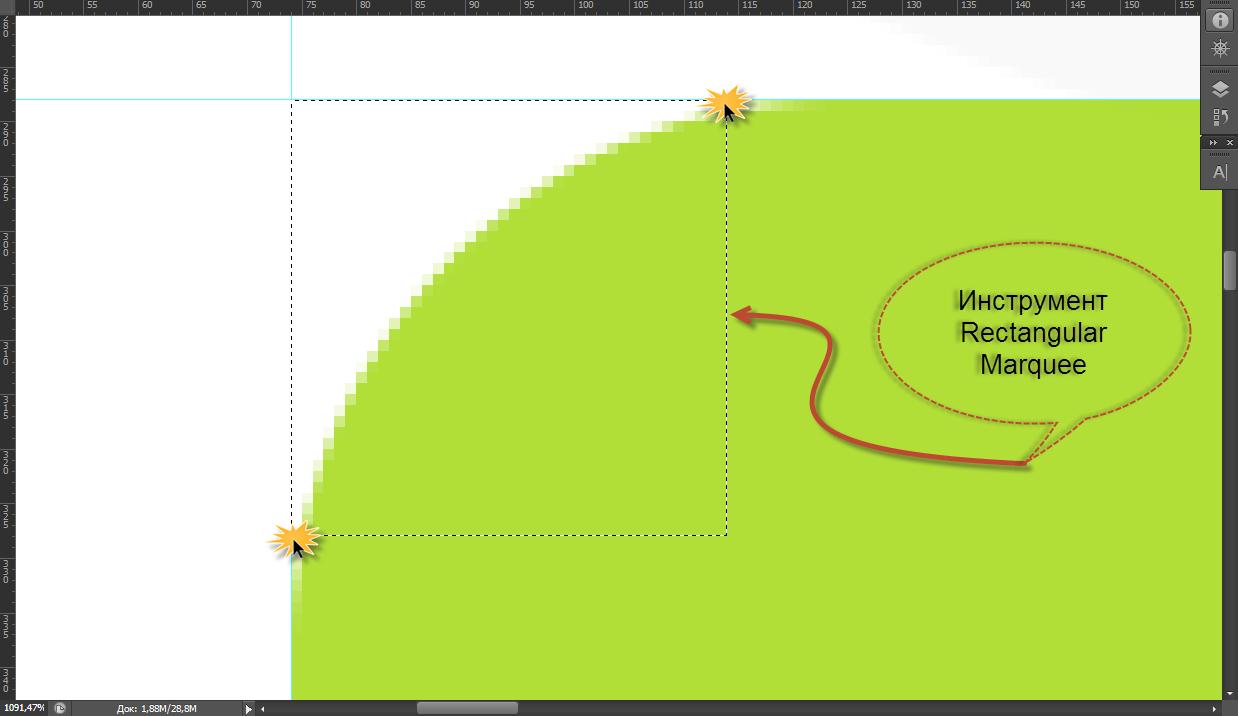
Можно выполнить построение другим способом. Начать выделение из одной точки (касательной) и закончить в другой, то есть, как бы по диагонали. Результат будет тот же самый, но не нужно создавать направляющие:
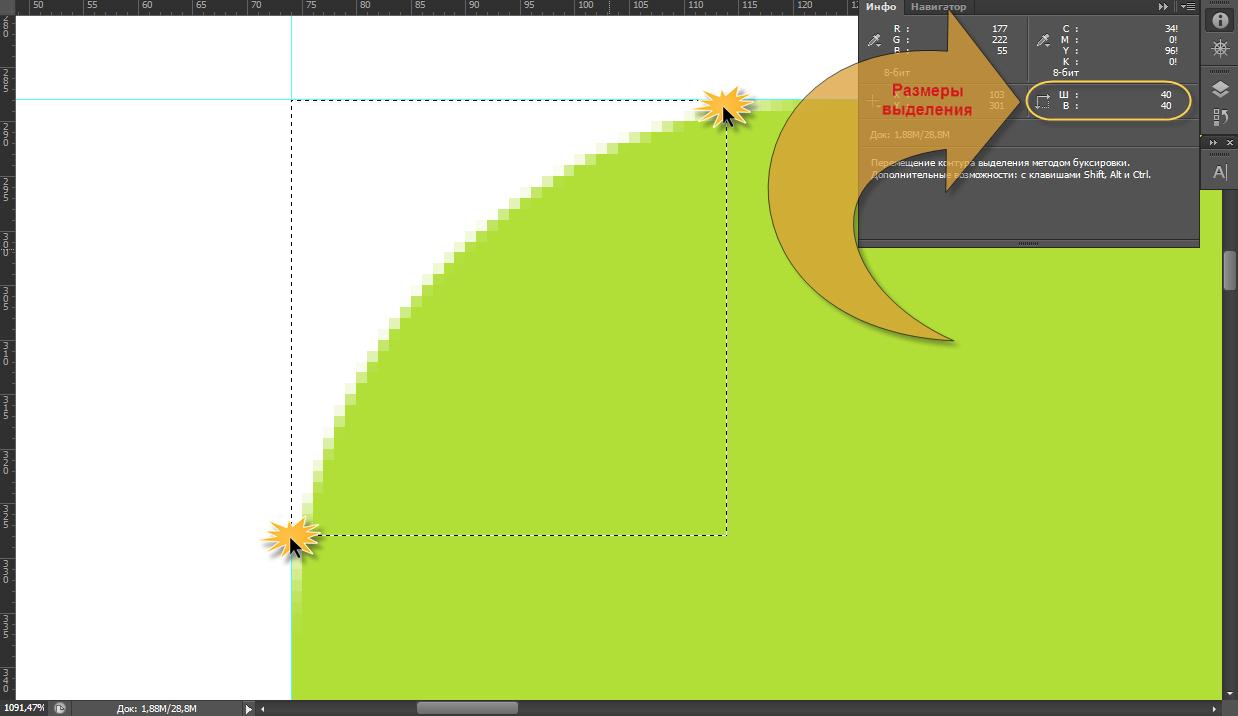
Теперь откроем панель “Инфо”, и взглянем на размеры построенного квадрата. Длины сторон и будут радиусом скругления для данного блока на макете:
При построении квадрата выделения на psd-макете бывает, что невозможно точно попасть так, чтобы стороны квадрата совпали с направляющими guideline. Для себя нашел такой выход. Ну, не попал, так не попал.
Как видно, все оказалось очень просто. Теперь, зная точное значение радиуса скругления, можно создать шаблон сайта, максимально соответсвующий psd-макету.
На рисунке с изображением круга и квадрата, созданных в AutoCAD, имеется неточность. В выноске указано, что построен прямоугольник, хотя на самом деле это конечно же квадрат.
Как узнать радиус скругления

| Математические головоломки | |||||
|---|---|---|---|---|---|
|
| Математический портал | ||
|---|---|---|
|
| Математика в афоризмах | ||||||
|---|---|---|---|---|---|---|
|
| Математические фокусы | |||||
|---|---|---|---|---|---|
|
| Занимательная арифметика | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
| Решение математических задач | ||||||
|---|---|---|---|---|---|---|
|
Д. Пойа
Серьезный человек, изучающий математику, намеревающийся сделать математику делом своей жизни, должен учиться доказательным рассуждениям, это его профессия и отличительный признак его науки. Однако для действительного успеха он должен учиться и правдоподобным рассуждениям; это тот тип рассуждений, от которого будет зависеть его творческая работа [247, с. 11].
Радиусы скруглений. Размеры и предельные отклонения
Источник: ОСТ 92-0093-69
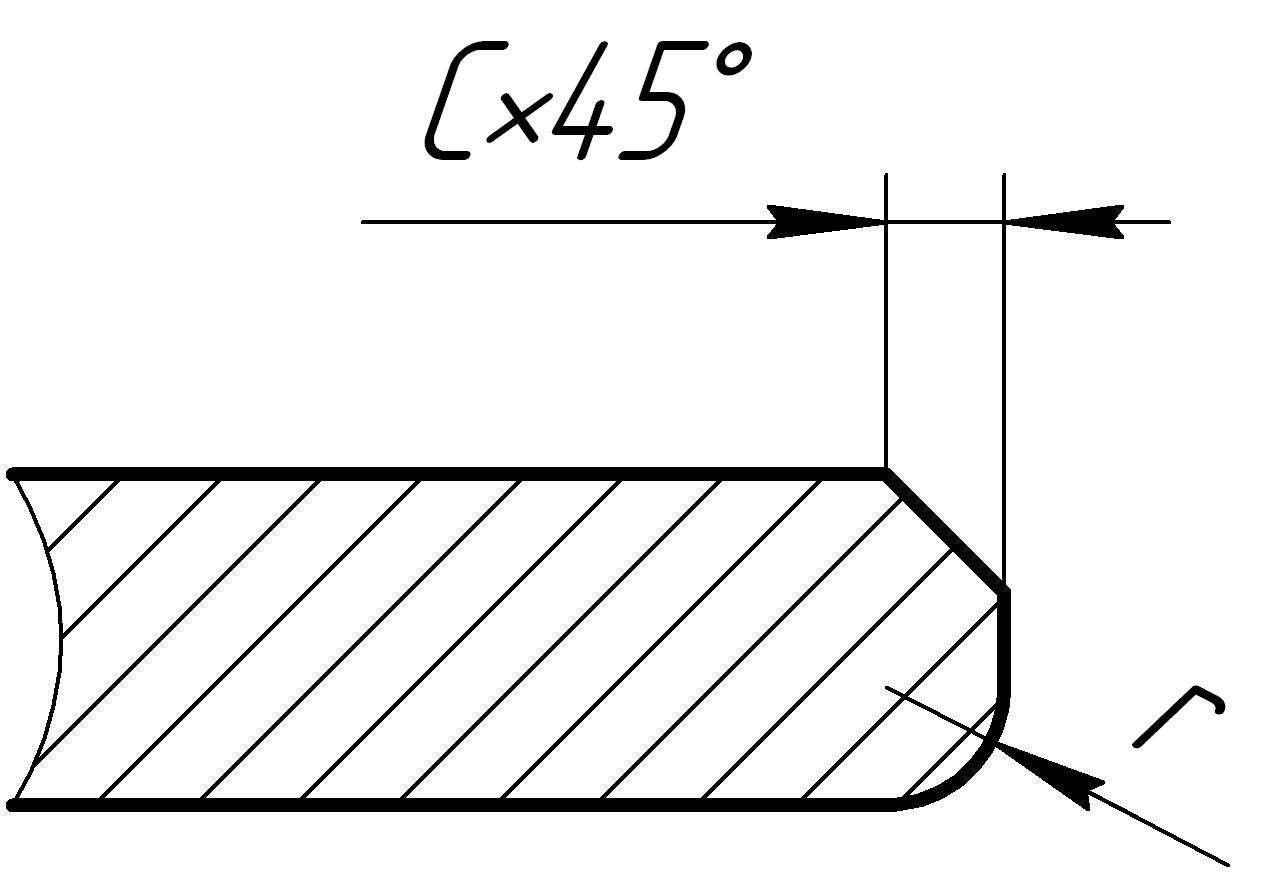
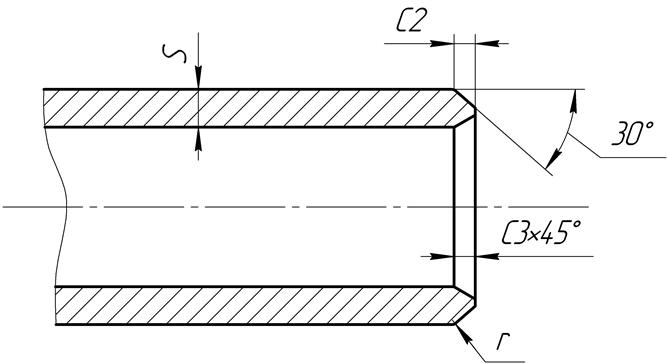
Рис 1. Размеры и предельные отклонения радиусов скруглений и фасок для сопряжений типа «вал – отверстие»
Таблица 1. Рекомендуемый подбор сопряжений радиуса с радиусом и радиуса с фаской, мм
Таблица 2. Размеры и предельные отклонения радиусов скруглений или фасок для сопрягаемых поверхностей валов и втулок, мм
При применении радиусов скруглений или фасок размером св. 6 до 10 мм предельное отклонение ±1,5 мм; св. 10 до 20 – ±2 мм; св. 20 до 32 – ±2,5 мм и свыше 32 – ±3 мм.
Таб 3. и Рис.2 Размеры и предельные отклонения радиусов скруглений валов и корпусов, сопрягаемых с шарико- и роликоподшипниками, мм
Рис 3. и Таб 4. Размеры фасок и радиусов и предельные отклонения на механически обрабатываемые плоские детали
Рис. 4 и Таб. 5. Размеры и предельные отклонения фасок на валах под запрессовку
Таб. 6
Рис. 5 и Таб.7. Размеры и предельные отклонения фасок на втулках под запрессовку
Примечание: величину радиуса скругления и предельные отклонения на него выбирать по таблице 5.
Размеры радиусов и фасок сопрягаемых поверхностей типа «вал – отверстие», валов и корпусов с шарико- и роликоподшипниками, а также валов и втулок под запрессовки, должны быть указаны в чертежах с числовыми значениями предельных отклонений.
Размеры радиусов скруглений и фасок несопрягаемых поверхностей валов и втулок и размеры фасок и радиусов на плоских деталях должны быть указаны в чертежах. Предельные отклонения этих размеров на изображении не наносятся, а в технических требованиях чертежа пишется: «Неуказанные предельные отклонения размеров радиусов и фасок по ОСТ 92-0093-69».
Предельные отклонения на угловые размеры фасок ± 3°.
К оглавлению
Главконструктор работает с компаниями в городах:
Санкт-Петербург, Москва, Севастополь, Воронеж, вся Россия.
Радиусы скруглений. Размеры и предельные отклонения
Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Я достаточно подробно ответил на ваш вопрос в статье «Расчет арочной перемычки», где вы задали подобный вопрос.
Сначала термины:
Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h).
Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2.
А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).