как узнать расстояние до объекта зная его размер
Измерения расстояний на местности
Человеку, находящемуся в какой-либо местности может понадобится возможность измерение расстояний до определенных объектов, а также определение ширины и высоты этих обьектов. Такие измерения лучше и точнее можно провести с иcпользованием специальных средств (лазерных дальномеров, дальномерных шкал оптический приборов и.т.д.), но таковые не всегда могут оказаться под руком. Поэтому в данной ситуации на выручку придет знание «дедовских», проверенных временем, способов.
К таковым относятся:
Определение расстояний на глаз;
По угловой величине;
По звуку;
Определение расстояний на глаз.
Данный способ является наиболее простым и быстрым способом. Определеяющим здесь является умение мысленно откладывать на местности равные отрезки в 50, 100, 500 и 1000 м. Данные отрезки расстояний необходимо изучить и хорошо закрепить в зрительной памяти. При этом необходимо принимать во внимание следующие особенности:
Дистанции более 1 км определяются с большей погрешностью, достигающей 50%. У опытных людей, собенно на малых дистанциях погрешность составляет менее 10%. Глазомер необходимо постоянно тренировать в различных условиях видимости, на различной местности. При этом огромную положительную роль вносит занятие туризмом, альпинизмом, охотой.
1 тысячная 0-01, читается как ноль, ноль один
5 тысячных 0-05, читается как ноль, ноль пять
10 тысячных 0-10, читается как ноль, десять
150 тысячных 1-50, читается как один, пятьдесят
1500 тысячных 15-00, читается как пятнадцать, ноль ноль
Для того, чтобы определить угловую величину, необходимо знать, что отрезок в 1 мм, удаленному на 50 см от глаза соответствует углу в 2 тысячные (0-02). На основании этого существует метод определения расстояний при помощи линейки:
1). Линейку с миллиметровыми делениями вытянуть на расстояние 50 см
2). Засечь, во сколько делений на линейке укладывается ширина или высота объекта.
3).Полученное кол-во миллиметров умножить на 2, и подставить в выше приведенную формулу
Еще удобней для этих целей использовать штангенциркуль, который для компактности можно укоротить.
Также существует более простая формула определения дистанции при помощи линейки:
Д = (высота или ширина объекта в см / кол-во миллиметров на линейке) x 5
Пример: ростовая фигура имеет высоту 170 см и на линейке закрывает 2 мм, следовательно дистанция до нее будет:(170см / 2мм) x 5 = 425 м

Определение расстояний при помощи линейки и сподручных предметов
| Объект | Высота, м | Длина, м |
| Телеграфный столб деревянный | 6 | —- |
| Телеграфный столб бетонный | 8 | —- |
| Расстояние между столбами ЛЭП 6м | —- | 50 |
| Расстояние между столбами высковольт. линий | —- | 100 |
| Товарный вагон, 4-х осный | 4 | 14-15 |
| Пассажирский вагон цельнометаллический | 4 | 24 |
| Цистерны, 2-х осные | 3 | 6,75 |
| Цистерны, 4-х осные | 3 | 9 |
| Один этаж панельного дома | 3 | —- |
| Дом сельского типа | 6-7 | —- |
| Высота железнодорожной будки | 4 | —- |
| Ростовая фигура (средн.) | 1,7 | —- |
| Голова без каски | 0,25 | 0,20 |
| Голова в каске | 0,30 | 0,30 |
| Танк | 2,5-3 | —- |
| Грузовой автомобиль | 2-2,5 | —- |
Линейные размеры распространенных объектов
При отсутствии линейки угловые величины можно измерять помощи подручных предметов, зная их линейные размеры. Это может быть, например спичечный коробок, спичка, карандаш, монета, патроны, пальцы рук и.т.д
Определение расстояний без специальных средств
Человеку, находящемуся в какой-либо местности может понадобится возможность измерения расстояний до определенных объектов, а также определение ширины и высоты этих обьектов. Такие измерения лучше и точнее можно провести с иcпользованием специальных средств (лазерных дальномеров, дальномерных шкал оптический приборов и.т.д.), но таковые не всегда могут оказаться под рукой. Поэтому в данной ситуации на выручку придет знание «дедовских», проверенных временем, способов. К таковым относятся:
Определение расстояний на глаз
Данный способ является наиболее простым и быстрым. Определяющим здесь является умение мысленно откладывать на местности равные отрезки в 50, 100, 500 и 1000 м. Данные отрезки расстояний необходимо изучить и хорошо закрепить в зрительной памяти. При этом необходимо принимать во внимание следующие особенности:
Еще удобней для этих целей использовать штангенциркуль, который для компактности можно укоротить.
Также существует более простая формула определения дистанции при помощи линейки:
Д = (высота или ширина объекта в см / кол-во миллиметров на линейке) x 5
Пример: ростовая фигура имеет высоту 170 см и на линейке закрывает 2 мм, следовательно дистанция до нее будет:(170см / 2мм) x 5 = 425 м
Определение расстояний при помощи линейки и сподручных предметов
Линейные размеры распространенных объектов
| Объект | Высота, м | Длина, м |
| Телеграфный столб деревянный | 6 | — |
| Телеграфный столб бетонный | 8 | — |
| Расстояние между столбами ЛЭП 6м | — | 50 |
| Расстояние между столбами высковольт. линий | — | 100 |
| Товарный вагон, 4-х осный | 4 | 14-15 |
| Пассажирский вагон цельнометаллический | 4 | 24 |
| Цистерны, 2-х осные | 3 | 6,75 |
| Цистерны, 4-х осные | 3 | 9 |
| Один этаж панельного дома | 3 | — |
| Дом сельского типа | 6-7 | — |
| Высота железнодорожной будки | 4 | — |
| Ростовая фигура (средн.) | 1,7 | — |
| Голова без каски | 0,25 | 0,20 |
| Голова в каске | 0,30 | 0,30 |
| Танк | 2,5-3 | — |
| Грузовой автомобиль | 2-2,5 | — |
При отсутствии линейки угловые величины можно измерять помощи подручных предметов, зная их линейные размеры. Это может быть, например спичечный коробок, спичка, карандаш, монета, патроны, пальцы рук и.т.д Например, спичечный коробок имеет длину — 45 мм, ширину 30 мм, высоты 15 мм, следовательно если его вытянуть на расстояние 50 см, его длина будет соответствовать 0-90, ширина 0-60, высота 0-30.
Определение расстояний по звуку
Человек обладает способностью улавливать и различать звуки различной природы, как в горизонтальной плоскости, так и в вертикальной, что позволяет весьма успешно навскидку определять расстояния до источников звука. Слух, как и глазомер необходимо постоянно тренировать.
Средняя дальность слышимости различных источников
| Объект | Расстояние, км |
| Выстрел их охотничьего ружья | 3,5 |
| Шум поезда | 10 |
| Паровозный гудок | 7-10 |
| Сигнал автомобиля | 2-3 |
| Рокот работающего трактора | 3-4 |
| Топот лошадей | 1-1,5 |
| Крики человека | 1-1,5 |
| Лай собак | 2-3 |
| Негромкая речь, шум шагов | 0,3-0,5 |
| Всплески от весел | 0,25-0,5 |
| Кашель | 0,05 |
| Движение автомобиля (ровный шум мотора) | 1 |
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Измерение расстояния до объекта и его скорости
Технологию, которую я собираюсь Вам представить, я не встречал в найденных мной методах определения расстояния до объекта на изображении. Она не является ни универсальной, ни сложной, суть её заключается в том, что видимое поле (будем считать, что мы используем видеокамеру) калибруется линейкой и затем сопоставляется координата объекта на изображении с отметкой на линейке. То есть измерение ведётся по одной линии или оси. Но нам не нужно хранить отметку на линейке для каждого пикселя, алгоритму для калибровки нужно только знать размер линейки в пикселях и в метрах, а также координату пикселя, который является фактической серединой линейки. Очевидное ограничение — работает только на плоских поверхностях.
Кроме самого метода в статье рассмотрена его реализация на языке Python с использованием библиотеки OpenCV, а также рассмотрены особенности получения изображений с вебкамер в Linux, используя video4linux2 API.
На практике нужно было измерить расстояние до автомобиля и его скорость на каком-нибудь прямом участке дороги. Я использовал длинную рулетку, растягивал её в доль дороги, по середине полотна, затем настраивал камеру так, чтобы вся рулетка как раз входила в поле зрение камеры и была выравнена с осью X изображения. Следующим шагом было положить что-нибудь яркое на середину рулетки, закрепить камеру так, чтобы она никуда не съехала, и записать координаты пикселя этой середины.
Все расчёты сводятся к одной единственной формуле:
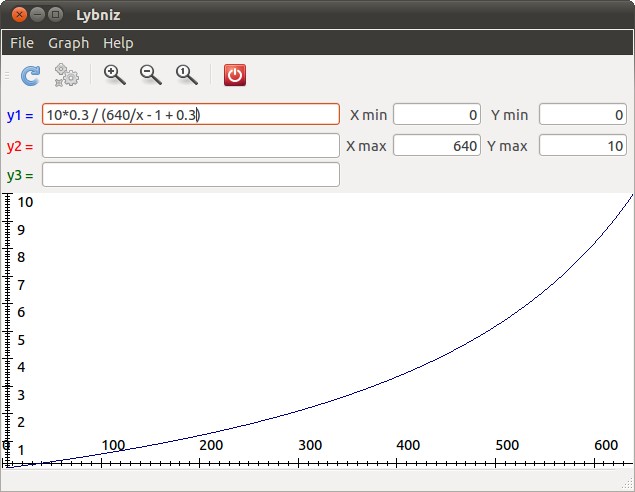
l = L*K / ( W/x — 1 + K ), где
l – искомое расстояние до объекта, м;
L – длина «линейки», м;
W – длина «линейки» в пикселях, обычно совпадает с шириной изображения;
x – координата объекта на изображении;
K = (W — M) / M – коэффициент, отражающий наклон камеры, здесь M – координата середины «линейки».
В выводе этой формулы мне очень пригодились школьные знания тригонометрии.
График зависимости этой функции приведён на рисунке:
Чем больше наклон камеры, тем круче идёт график. В граничном случае, когда ось камеры направлена перпендикулярно плоскости «линейки» ( M = W / 2), график становится прямой линией.
Но статья была бы слишком короткой, если бы на этом и остановиться. Поэтому я решил сделать демонстрационную программу, которая бы подключалась к вебкамере компьютера и следила бы за каким-нибудь объектом, вычисляя расстояние до него и его скорость. В качестве языка программирования я выбрал Python, язык с очень большим количеством достоинств, для построения графического интерфейса был выбрал фреймворк Tkinter, идущий вместе с Python, так что его не нужно устанавливать отдельно. Для слежения за объектом хорошо подходит OpenCV, я использую версию 2.2, но в репозитории текущей версии ubuntu (10.10) имеется только версия 2.1, а у них API немного изменилось в лучшую сторону и программа под версией 2.1 не заработает. В принципе можно было бы построить всю программу на OpenCV, возложив на неё функции графического интерфейса и захвата изображения, но я хотел отделить её от основной части программы, чтобы можно было если что заменить эту библиотеку на что-нибудь другое или просто убрать, выключив слежение. Я начал перерабатывать старую программу, удаляя всё ненужное, и на моё удивление от программы осталось всего несколько строк с непосредственным расчётом расстояния и скорости, что в принципе было логично, так как в оригинале программа не использует графический интерфейс, следит за автомобилем по другому алгоритму да и вместо вебкамеры используется мегапиксельная сетевая камера с подключением по RTSP.
Что касается получения изображений с вебкамеры, то тут не всё так просто. Под Windows программа использует DirectX для подключения к камере через библиотеку VideoCapture, здесь всё достаточно просто. Но под Linux внятных статей об использовании вебкамер из Python очень мало, а те примеры что есть как правило оказываются неработоспособными из-за какой-нибудь очередной смены API. В прошлом я использовал ffmpeg для этих целей и программа была на C, но ffmpeg это немного «по воробьям из пушки», да и дополнительными зависимостями не хотелось отягощать конечную программу. Можно было воспользоваться OpenCV, которая так же использует ffmpeg, но был выбран путь написания собственной обёртки video4linux2 API для Python.
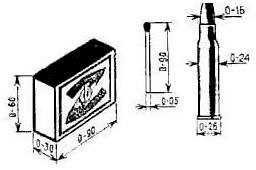
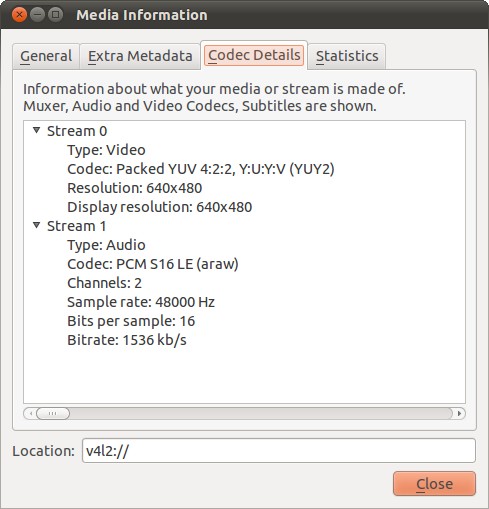
Также подразумевается, что вебкамера отдаёт изображение в YUYV формате (YUV422), от RGB он отличается тем, что цветовой информации в нём в 2 раза меньше. В YUYV два пикселя кодируются 4 байтами, а в RGB шестью, отсюда экономия в полтора раза. Y — компонента яркости, для каждого пикселя она своя. U и V — цветоразностные компоненты, которые определяют цвет пикселя, так вот каждые два пикселя используют одни и те же значения U и V. Если представить поток байт от вебкамеры в этих обозначениях, то он будет выглядеть как YUYV YUYV YUYV YUYV YUYV YUYV — это 12 пикселей. Выяснить в каком формате у Вас работает вебкамера можно с помощью VLC плеера, открываете захватывающее устройство с его помощью и затем запрашиваете информацию о кодеке, должно быть как на рисунке:
Вот так выглядит исходный код библиотеки для доступа к вебкамере:
main_v4l2.cpp
Алгоритм вполне понятен — сначала открываем устройство, имя которого задаётся вначале («/dev/video0»), а затем на каждый запрос getFrame считываем кадр с вебкамеры, конвертируем его в RGB формат и отдаём ссылку на кадр тому, кто его просил. Я предоставляю также Makefile для быстрой компиляции данной библиотеки, если вам это понадобится.
А вот так выглядит обёртка этой библиотеки для Python:
v4l2.py
Как видите абсолютно ничего сложного. Библиотека подключается с помощью модуля ctypes. В написании обёртки не было никаких проблем, за исключением строчки:
Осталось только показать исходный код основного скрипта, который формирует графический интерфейс и загружает все остальные модули.
main.py
Способы определения расстояний без специальных средств
Ведёте ли вы автомобиль, путешествуете ли с рюкзаком, умение определять расстояния — это важный и полезный навык, как в городе, так и в дали от городской суеты. В данной статье, я расскажу о том, как рассчитывать расстояния и тренировать глазомер.
Варианты определения расстояний до объектов
Среди полезных умений, которые рекомендуется освоить всем, кто предпочитает спокойному отдыху активный, относится определение расстояния на местности. Ситуаций, когда этот навык может пригодиться, множество – отсутствие картографического материала или его порча, утеря, необходимость определить ширину реки на глаз, расстояние до цели, произвести расчет высоты дерева, которое нужно использовать в качестве моста и другое.

Существующие варианты отличаются различной погрешностью измерений и инструментарием. Узнать расстояние можно:
Определение расстояния «на глаз» или по линейным объектам
Метод измерения расстояния «на глаз» подходит, когда есть объект с известным размером (длина, ширина или высота). Такой расчет считается точным на 90%, а иногда и больше, если набраться опыта.
Линейные размеры самых часто встречающихся объектов:
L Как определять стороны света в природе, рассказываю в статье: Как определить север и юг без компаса днем и ночью
Как определить расстояние до объекта
Возьмите линейку и расположите ее на уровне измеряемого объекта в 50 см от глаз. Размеры предмета (длину, ширину или высоту) измеряют по линейке и учитывают в миллиметрах.

Теперь воспользуйтесь формулой:
Расстояние, м =(реальный размер в см/измеренный размер по линейке в мм)*5.
Этот академический метод в туристической среде был немного упрощен. Определение расстояния туристы проводят по большому пальцу.
Рассмотрим на примере измерения расстояния до столба связи (высота 8 м). Длина большого пальца около 6 см. Вытяните руку перед собой, сожмите ладонь в кулак так, чтобы большой палец смотрел вверх. Расстояние от глаз до пальца будет около 60 см. Определите какой длине соответствует столб, к примеру трети пальца (2 см).
Далее осталось рассчитать пропорцию:
Х = (8 м * 60 см)/2 см =240 м.
Вычисление расстояния шагами
Умение определять расстояния собственными шагами может пригодиться как для любителей туризма (например, при составлении схем местности и наоборот, при поиске объекта, указанного на карте или плане), так и обычным горожанам, которые занимаются, скажем, спортивной ходьбой.

Шаги используют в качестве мерной единицы по причине того, что человек обычно делает одинаковые по длине шаги, когда идет размеренным шагом по ровной поверхности. Именно эту длину своего шага рекомендуется вычислить и запомнить, как эталонную.
На изменение эталонной длины влияет:

Смысл такого измерения в том, что нужно «наследить» мокрыми ногами, затем взять рулетку и узнать расстояние от одной пятки до другой. Для чистоты расчетов, следует сделать несколько шагов, померить расстояния и вычислить среднее значение.
Имея длину шага, теперь можно без труда считать расстояния в походе или на прогулке. Интересно, что если ввести такой подсчет в привычку, то скоро вы заметите, что считаете шаги уже по инерции. Есть два способа учитывать шаги.
Чтобы не сбиться при подсчете, когда количество шагов переваливает за отметку 100, можно на каждую сотню загибать палец или перекладывать спички из одного кармана в другой.
Видимость объектов – как способ узнать расстояние
По тому различимы объекты, находящиеся вдали глазом или нет, также можно достаточно точно определять расстояние. Тренировкой возможно добиться снижения погрешности в определении длины до 10-20% на 1 км.

Используя этот метод, нужно учитывать, что глаз по-разному воспринимает расстояния:
Данные, приведенные ниже, рассчитаны на определение расстояния до объекта днем в ясную погоду на равнинной местности.
L Как определить погоду в походных условиях, вы узнаете из статьи: Способы как узнать погоду по приметам на завтра
Заключение
В походе нет неважных навыков. Чем больше вы умеете, тем уверенней вы себя чувствуете, особенно в экстремальных ситуациях. Точно определять расстояния «на глаз» можно научиться, всего лишь чаще тренируйте свой глазомер, используя методы, описанные в данной статье.
 bootsector
bootsector
Ретротехника, самоделки и борьба с идиотизмом
В связи с известным событием по всему интернету развернулись бурные дискуссии, участники которых обвиняют своих оппонентов то в незнании программы средней школы, то в непонимании того очевидного факта, что в военное время косинус угла может достигать четырёх.
Не желая в эти дискуссии ввязываться, я лучше на наглядном примере покажу вам, как, имея на руках фотографию какого-либо известного объекта и немного вспомогательной информации, можно с большой точностью по совсем не сложным формулам рассчитать, на каком расстоянии этот объект находился от фотографа в момент съёмки. По возможности я постараюсь каждый шаг сопровождать иллюстрацией, расчётом или ссылкой на источник. Итак, приступим.
Как известно, простейший объектив для фотоаппарата можно сделать из одной двояковыпуклой линзы. Конечно, существуют фотоаппараты вообще без объектива (так называемые пинхол-камеры, предок которых — камера-обскура), но в данном случае они нам не слишком интересны. Для начала мы рассмотрим, как строится изображение в простейшем однолинзовом объективе, а затем я покажу, что те же методы хорошо подходят и для сложных объективов, сочетающих в себе более десятка последовательно расположенных линз.
Напомню вам схему хода лучей в тонкой линзе из школьного курса геометрической оптики:
На этой схеме d — расстояние от линзы до объекта, D — расстояние от линзы до изображения объекта (на матрице или плёнке), а f — фокусное расстояние линзы.
Формула тонкой линзы из того же курса связывает эти три расстояния:
Теперь ещё раз посмотрим на оптическую схему: h — это линейный размер объекта съёмки, а H — размер его уменьшенного изображения. Нетрудно заметить, что h = d tan α, а H = D tan α (это следует из свойств прямоугольного треугольника). Подставив эти величины в формулу тонкой линзы, увидим, что tan α сокращается, и в результате получим следующее уравнение:
«Неудобная» величина D ушла, а остальные мы знаем или можем легко вычислить. На основе этого уравнения получаем вот такую формулу расстояния до объекта:
Ну а теперь давайте проверим её на практике.
Вот фотография, которую я сделал из своего окна:
На ней запечатлён дом 1 по 3-му Дорожному проезду, что в Москве. Это 22-этажная башня серии И-700А.
Какую полезную информацию можно извлечь из данной фотографии? Напомню, для расчёта нам нужны неизвестные пока величины h, H и f. h — это реальная высота дома (в метрах). Сходу я её не нагуглил, зато выяснил вот что: высота потолков в этом доме — 2,64 м, а толщина перекрытий — 0,22 м. Наверняка при измерении высоты потолков не учитывалась толщина напольного покрытия. Точно она мне не известна, так что, немного округлив, примем высоту одного этажа равной 2,9 м. Хорошо видны 23 панели, таким образом, высота видимого участка составляет примерно 66,7 м. Запомним эту величину и приступим к анализу фотографии.
H — это размер изображения дома на матрице фотоаппарата. По фотографии мы можем подсчитать его в пикселях, но, как известно, размер пикселя — это всё равно что размер ангела: точных данных ни у кого нет. Но здесь нужно вспомнить, что конкретные физические размеры имеет матрица фотоаппарата. Лезем в поисковик и узнаём, что для камеры Nikon D90 размер матрицы составляет 2,36 × 1,58 см, а разрешение — 4288 × 2848 пикс. Наша фотография не была кадрирована или повёрнута, поэтому мы можем узнать точный линейный размер изображения дома на матрице, составив пропорцию. Но чтобы делать это не вручную, воспользуемся программой Adobe Photoshop, где есть масса полезных инструментов.
По умолчанию Photoshop, конечно, не знает, какого размера должна быть наша фотография, и указывает ей разрешение 300 пикс./дюйм, или 118,11 пикс./см:
Но мы, зная физический размер матрицы и количество пикселей по длинной стороне снимка, делаем такой расчёт: 4288 / 2,36 (размер матрицы в сантиметрах), и получаем правильное разрешение — 1817 пикс./см. Вписываем его в соответствующее окошко и, чтобы не изменились реальные размеры фотографии, а лишь были пересчитаны её длина и ширина в см, указываем в верхних полях «100 проц»:
Как видите, при этом в поле «Размер печатного оттиска» появились уже известные нам размеры матрицы: 2,36 × 1,57 см. Точнее, в спецификации было указано 1,58 см, но это несущественная погрешность.
Теперь при помощи инструмента «Линейка» измерим высоту видимого участка дома (23 панели) на фотографии (смотрите в правый верхний угол):
Получается, что высота изображения дома на матрице составляет 1,92 см, или 0,0192 м.
Осталось только выяснить фокусное расстояние, но для этого, к счастью, ничего считать не нужно: оно сразу прописывается при съёмке в метаданных фотографии (EXIF). Открываем их в фоторедакторе и видим:
Фокусное расстояние при съёмке составляло 105 мм, или 0,105 м, то есть я снимал дом с максимально возможным для этого объектива приближением.
Ну что ж, теперь у нас есть все данные для расчёта. Подставляем их в формулу
и получаем: d = (0,105(0,0192 + 66,7)) / 0,0192 = 364,9 м. Внимательный читатель наверняка заметил, сколь ничтожно мала величина H в сравнении с h, поэтому нашу формулу смело можно упростить до вида
Для любых фотографий относительно крупных объектов, сделанных с расстояния больше 10 м, она будет давать практически тот же результат.
Ну а теперь самое интересное — нужно проверить, верна ли была использованная нами формула? Ведь в начале я говорил, что мы рассматриваем упрощённую конструкцию объектива, а не реальную. Может быть, наши расчёты не имеют ничего общего с действительностью? К счастью, это легко выяснить. Заходим на Яндекс.Карты и переходим в точку с координатами 55.604364, 37.611455. Затем активируем инструмент «Линейка» и ставим на карте две точки: одну — возле окна, из которого было сделано фото, а другую — возле стены дома, на которой мы считали панели:
Получаем 365 м. Ну не красота, а? Величины совпали с точностью до 0,1 м! Конечно, такая точность в известной мере является результатом везения, потому что и при измерении размеров изображения, и при подсчёте высоты этажей, и при расстановке точек на карте я вполне мог допускать погрешности в 1–3%. Но, как бы то ни было, в конечном итоге расчётная и измеренная величины сошлись.
Скептически настроенный читатель может подумать, что я подгонял цифры, и что для другой фотографии всё будет по-другому. Что ж, у меня есть ещё одно фото того же дома, сделанное с аналогичной точки, но совсем с другим фокусным расстоянием:
Проделаем для него те же измерения и расчёты. У меня получилось, что размер изображения дома составляет 0,39 см, а фокусное расстояние — 21 мм. Подставляем эти числа в упрощённую формулу и получаем d = (0,021 × 66,7) / 0,0039 = 359,2 м. Результат немного отличается, но всё равно в рамках погрешности совпадает с измеренным по карте. Расхождение несложно объяснить: камера указывает фокусное расстояние как целое число, то есть и 20,51, и 21,49 мм она покажет как 21 мм. А это уже даёт погрешность 2,4%.
Впрочем, самых въедливых скептиков наверняка не убедил и этот пример. Ведь в обоих случаях я использовал один и тот же объектив — а что, если формула работает для него чисто по совпадению? Справедливое замечание. Чтобы проверить, так ли это, я возьму кадр, сделанный не только другим объективом, но и другим фотоаппаратом, причём не цифровым, а плёночным.
Вот фотография, которую мы будем анализировать:
Её много лет назад сделал мой отец на свой «Зенит-Е» с объективом Гелиос-44-2. Фокусное расстояние этого объектива составляет 58 мм. Определить физический размер изображения дома очень просто: у меня есть слайд, который я оцифровал с определённым разрешением, и сканер прописал его в свойствах файла. Тут даже пересчитывать ничего не нужно, достаточно воспользоваться линейкой.
Участок из тех же 23-х панелей имеет на слайде высоту 1,06 см. Подставляем значения в формулу: d = (0,058 × 66,7) / 0,0106 = 365 м. Полное совпадение!
Что ж, мы получили интересные результаты: выходит, простая формула для тонкой линзы позволяет получать весьма точные (и легко проверяемые) результаты при анализе реальных фотографий, а не «сферических коней в вакууме». Почему же так происходит, если реальный объектив представляет собой не одну линзу, а целый бутерброд из линз? Ответ на этот вопрос поможет дать статья Википедии. Для сложного объектива при расчёте вводят не одну, а две главные плоскости. Фактически, расстояния d и D, которые вы видели на схеме в самом начале этого поста, в этом случае отсчитываются от разных (хотя и не слишком удалённых друг от друга) точек. Но расстояние D, даже небольшое изменение которого могло бы существенно повлиять на результат просто в силу небольших размеров этого плеча оптической системы, нам, к счастью, знать не нужно, потому что производитель объектива уже рассчитал и нанёс на его корпус фокусное расстояние, через которое величину D, как было показано выше, легко выразить. А что касается изменения расстояния от передней главной плоскости до объекта, то какими бы толстыми ни были линзы и каким бы длинным ни был объектив (мы, конечно, говорим о реальных конструкциях, а не воображаемых объективах размером с дом), при расстоянии до объекта съёмки в несколько сотен метров, как в нашем случае, величиной в десяток-другой сантиметров можно смело пренебречь.
На основании вышеизложенного легко вывести формулу для соотношения расстояний до объектов, запечатлённых на одной и той же фотографии. Причём знать фокусное расстояние объектива и размер матрицы в этом случае уже будет не нужно, поскольку они сократятся при составлении пропорции.
Как видите, даже знаний из программы средней школы достаточно, чтобы убедиться в полной некомпетентности отдельных «экспертов». Любите математику и не давайте себя обмануть!



 bootsector
bootsector



