как узнать размер матрицы
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
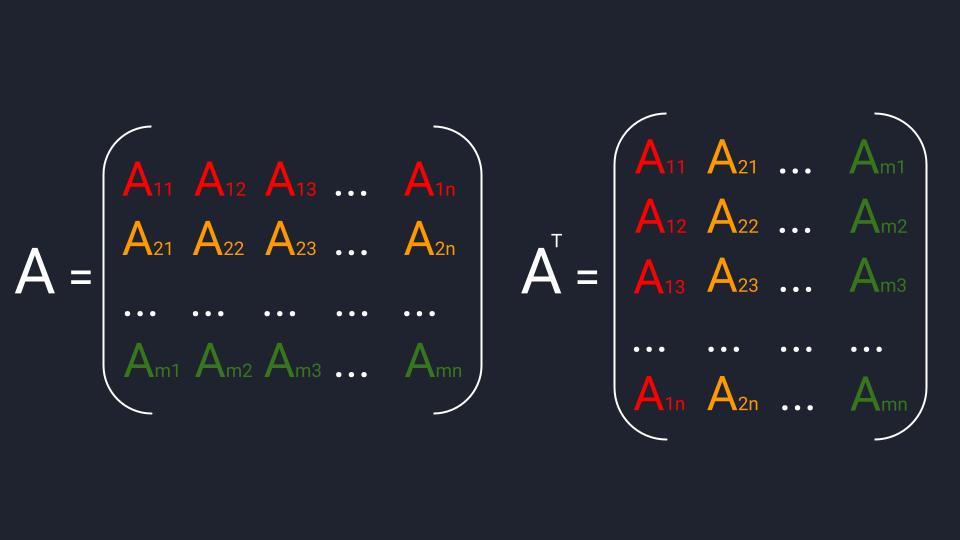
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Знакомство с матрицами
Понятие и базовые операции.
Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.
Общая схема матрицы 
Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три
Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре 
Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений
Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.
Пример умножения матрицы на число
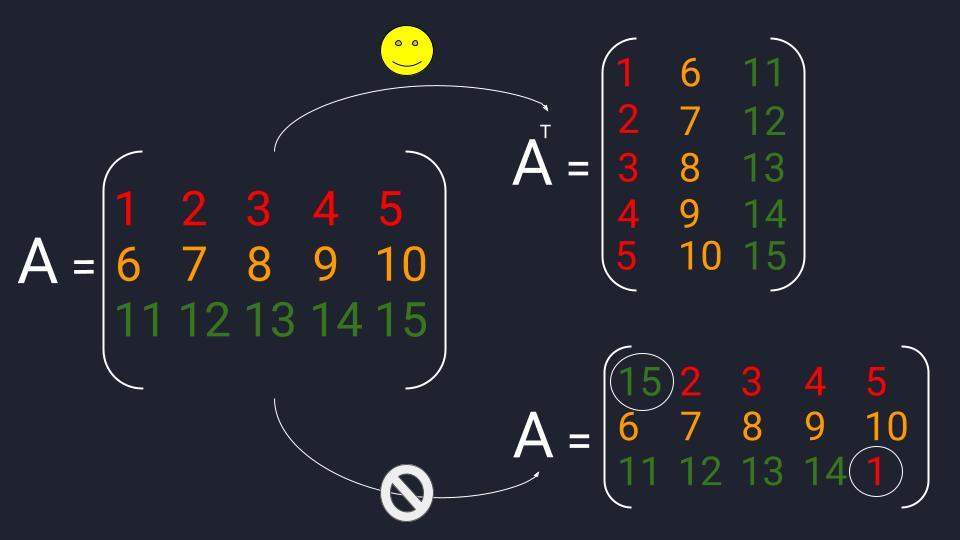
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.
Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы 
Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» 
Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил
Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами 
Пример вычитания двух матриц
Умножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
Формула умножения матриц 
Пример умножения квадратных матриц размерностью 2×2
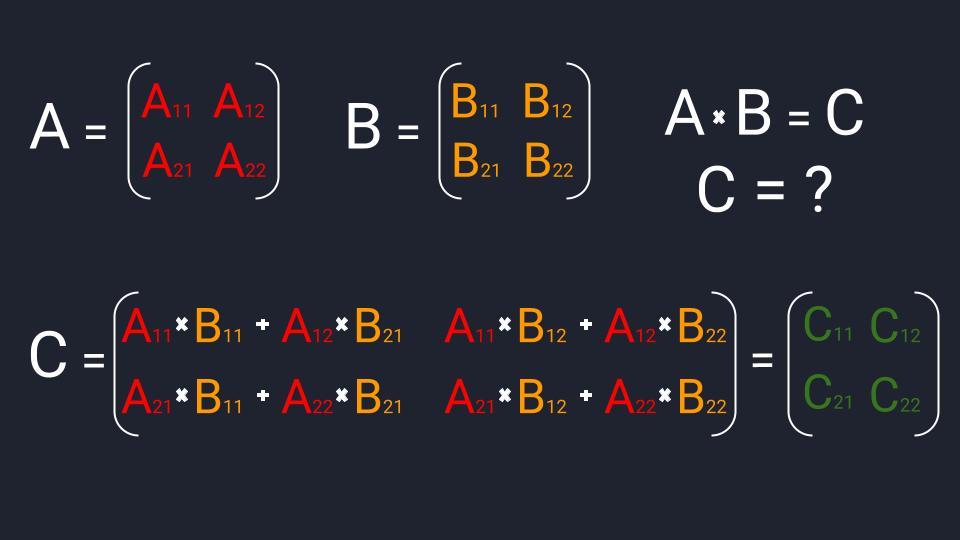
Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽
Камера смартфона для «чайников» №3. Погружаемся в матрицу!
Мы продолжаем погружаться в удивительный мир фотографии и в этой части подробно поговорим не только о матрицах и пикселях, но и о мобильной фотографии в целом.
Моя статья о влагозащите фитнес-браслетов для многих стала откровением, так как противоречила всему тому, о чем писали другие сайты. Эта статья, надеюсь, вызовет похожий эффект.
Проблема с интернетом заключается в том, что при смене технологий, популярные ресурсы не удаляют старый материал (да и с чего бы им это делать?). Затем приходят молодые авторы, читают и пересказывают информацию, которая уже давно не соответствует действительности.
Так было с часами и влагозащитой. В 2010 году многое изменилось, но куда девать все те статьи, что были написаны в течение двух предыдущих десятилетий? То же происходит и с камерами. Каждый человек видит просто феноменальный прорыв в области мобильных камер за последнее десятилетие, но продолжает повторять одну и ту же ерунду о маленьких матрицах и прочих ограничениях камерофонов.
Пришло время разобраться, на что именно влияет размер матрицы и пикселя, что такое шум и от чего он зависит, почему современные смартфоны снимают гораздо лучше, чем первые мобильные камеры и можно ли уменьшать размеры, увеличивая качество.
Чтобы сделать эту статью максимально понятной, я постараюсь избегать сложных терминов, заменяя их более простыми аналогиями. Тем не менее, информации будет очень много, поэтому на легкое чтение рассчитывать не стоит.
Для тех, кто попал сюда впервые
Вначале давайте вкратце вспомним, о чем говорилось ранее. В первой части мы разобрались с тем, каким образом свет переносит изображение в пространстве. Как оказалось, даже через окна в наши дома попадает не «простой свет», а картинка всего того, что происходит за окном. Но так как окна слишком большие, эта картинка получается настолько размытой, что мы не видим никаких четких очертаний.
У камеры смартфона есть такое же окошко — небольшое отверстие в объективе, через которое свет попадает внутрь устройства. Размер этого окошка обозначается в характеристиках смартфона буквами f/1.8 или f/2.4. Первая часть подробно объяснила, как понимать эти значения и на что они влияют.
Во второй части мы проследили за тем, что происходит дальше, когда свет прошел через отверстие объектива. В частности, мы детально рассмотрели, чем отличаются объективы смартфонов, что такое фокусное расстояние, за счет чего происходит приближение картинки и как определить настоящий (оптический) зум.
Вторая часть объяснила еще один важный параметр любой камеры, который в характеристиках указывается в миллиметрах, например, 26 мм или 130 мм.
Если посмотреть на типичные характеристики камеры любого смартфона, то мы увидим, что осталось еще много непонятных букв и цифр:
Основная камера: 108 Мп, 1/1.33″, f/1.8, 26 мм, 0.8 мкм, PDAF
В этой части я расскажу, как понимать характеристики, выделенные жирным шрифтом. Все они относятся к матрице: ее размерам, количеству пикселей и размеру одного пикселя.
Собираем отпечатки света
Для начала нужно понять, каким образом свет, прошедший через объектив и попавший на матрицу камеры, оставляет там свои «следы».
Если кто-то не знает, матрица — это аналог пленки, на которую объектив камеры проецирует изображение. Если бы вместо матрицы мы просто разместили белый фон, на нем бы точно также появилось качественное цветное изображение, но вот сохранить его нам бы не удалось.
Вместо белого фона мы размещаем специальную пластинку, сделанную из песка. Точнее, делается она из кремния, а кремний в соединении с кислородом (диоксид кремния) и есть песок.
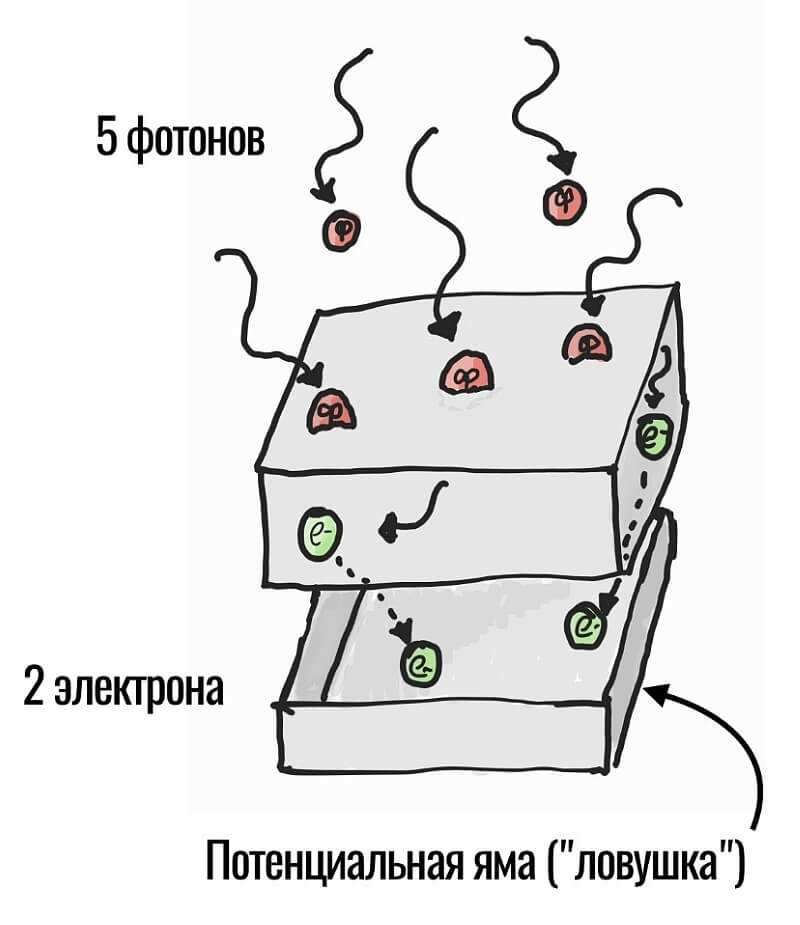
Так вот, если специально обработать чистый кремний и подключить к нему небольшое питание, можно добиться от него очень интересного поведения. Когда фотон (мельчайшая частичка света) попадает на такую пластинку, он поглощается кремнием и тут же высвобождает электрон:
Правда, фотон должен обладать достаточной энергией, чтобы выбить электрон из атома кремния, поэтому поглощается далеко не весь свет, а только тот, длина волны которого колеблется в пределах примерно от 400 до 1100 нанометров. И так уж совпало, что видимый нами свет идеально попадает в этот диапазон.
Матрица камеры смартфона состоит из миллионов крохотных пикселей — таких вот необычных кусочков кремния, реагирующих на свет. Помимо светочувствительного кремния, пиксель содержит еще множество других элементов, но для простоты восприятия пока упустим эти детали.
Итак, фотон успешно проник внутрь кремния и, «растворившись» в нём, образовал один электрон. Что же происходит с этим электроном дальше? Он попадает в специальную ловушку и оказывается на дне потенциальной ямы, выбраться самостоятельно из которой очень непросто.
Бывают ситуации, когда фотон подлетает к пикселю, но это не приводит к появлению электрона. Почему? Причины могут быть разными. К примеру, если длина волны этого фотона очень короткая, он будет поглощен еще в самом верхнем слое пикселя, а для очень длинной световой волны кремний и вовсе окажется прозрачным, фотон пролетит его насквозь, даже не заметив.
И здесь мы подходим к первому важному понятию, которое частично объясняет, почему современные смартфоны снимают так хорошо — это квантовая эффективность пикселя. Звучит страшно, но по сути это очень простое явление.
Если к поверхности пикселя подлетают 10 фотонов, но только 3 из них поглощаются кремнием (и, соответственно, высвобождаются 3 электрона), то 7 фотонов просто потерялись. Они оказались бесполезными. Получается, эффективность такого пикселя составила всего 30%, то есть, только 3 из 10 фотонов, попадающих на пиксель, будут высвобождать электроны. А значит, квантовая эффективность равняется 30%.
Исследовательские центры крупных производителей смартфонов постоянно работают над увеличением этого показателя.
Одним из главных «врагов» квантовой эффективности в матрицах являются перегородки между пикселями, которые позволяют избежать перекрестных помех (когда фотоны из одного пикселя попадают на другой). Находя новые (более светоотражающие) материалы для этих перегородок помимо всего прочего значительно улучшают данную характеристику.
Если в «древности» квантовая эффективность не превышала 10%, то в современных мобильных матрицах она легко превышает 85% в зависимости от длины волны света.
Еще каких-то пару лет назад квантовая эффективность пикселей была на 20-30% ниже. Получается, пиксели уменьшаются, а их квантовая эффективность возрастает. То есть, современный маленький пиксель будет более светочувствительным, нежели крупный пиксель старого камерофона.
Но вернемся к нашим электронам на дне ямы. В момент, когда происходит снимок, каждый из миллионов пикселей на матрице начинает ловить фотоны и поглощать их, высвобождая при этом электроны, которые сваливаются в ловушки. Снимок сделан!
Теперь камере нужно просто подсчитать, какое количество электронов оказалось в потенциальной яме каждого пикселя. Чем больше этих электронов, тем ярче будет нарисована соответствующая этому пикселю точка на фотографии. Именно так свет превращается в картинку.
Маленький или большой пиксель — что лучше?
Предположим, у нас есть две матрицы одного физического размера. На первой из них размещено 12 миллионов крупных пикселей (12 Мп), а на второй — в несколько раз больше, но размером они поменьше.
И возникает вопрос — есть ли какая-то разница между этими матрицами? Ведь они обе имеют один и тот же физический размер, а пиксели покрывают всю площадь.
Я сразу хочу отбросить теорию о том, что между пикселями есть пространство и много света просто теряется, так как он не попадает на светочувствительный элемент. Да, пространство между пикселями действительно есть, кроме того, внутри самого пикселя далеко не вся поверхность — это светочувствительный кремний.
Однако над каждым пикселем установлена специальная микролинза, которая собирает весь свет и фокусирует его на кремний:
И если раньше даже между линзами были какие-то зазоры, то сейчас их нет вовсе и расстояние между пикселями не играет никакой роли.
Теперь давайте определимся с терминами. Размер одного пикселя практически всегда указывается в характеристиках любого смартфона. Если вы посмотрите на параметры камеры, которые я приводил вначале, то увидите, что размер пикселя там составляет 0.8 мкм (микрометра). Есть пиксели размером 1 мкм, есть и более крупные, например, 1.4 мкм и даже 1.8 мкм (в Samsung Galaxy S20 или Sony Xperia 1 II).
И здесь любой профессиональный фотограф скажет вам, что размер пикселя важнее их количества. Почему? На это есть две причины.
Размер ловушки
Когда мы делаем снимок, в ловушку попадают электроны. Естественно, потенциальная яма пикселя не резиновая и в зависимости от освещения очень быстро заполняется до отказа. Если снимок всё еще делается, новые электроны будут попадать в яму и сразу же «вываливаться» оттуда в специально отведенное место — эдакий дренаж.
Одной из самых популярных мобильных матриц 2019-2020 гг является Sony IMX586. Она установлена в огромном количестве самых разных моделей от средне-бюджетного до премиального сегмента. В наших обзорах она также встречалась очень часто.
Так вот, размер пикселя этой матрицы составляет 0.8 микрометра, а емкость потенциальной ямы — минимум 4500 электронов. Если в ловушке уже оказалось 5000 электронов, а смартфон еще продолжает делать снимок, принимая новые фотоны света, этот пиксель будет переполнен и уже никакой информации, кроме яркой белой точки, в этом месте на снимке не будет.
В другом популярном сенсоре от Samsung на 64 Мп (используется в Redmi Note 8/9 Pro, Galaxy S20, Galaxy Note20) емкость потенциальной ямы — 6000 электронов.
Для сравнения, емкость потенциальной ямы одного пикселя многих зеркальных камер составляет 25 тысяч электронов, что всего в 4-5 раз больше микроскопических пикселей (0.8 мкм) от Sony и Samsung.
Основная задача таких внушительных «ловушек» — обеспечить широчайший динамический диапазон. То есть, чтобы на снимке не было ни одной белой точки с потерянными деталями. Посмотрите на эти две фотографии с разным динамическим диапазоном:
Слева мы видим, как пиксели, отвечающие за цвет неба в правом углу и плитку на полу, не справились со своей задачей. Их ловушки электронов просто переполнились от огромного количества фотонов, прилетевших с неба и отразившихся от плитки. А вот на снимке справа у пикселей оказались достаточно глубокие ловушки, что позволило рассмотреть детали даже в самых светлых областях.
Но этой проблемы практически не существует сегодня в мире смартфонов. Дело в том, что ее научились компенсировать двумя способами:
Выходит, даже маленькие пиксели по 0.8 мкм идеально справляются с динамическим диапазоном. Но, есть и другая проблема.
Ах эти грязные фотоны! Или откуда шум на снимках?
Оказывается, на снимках откуда-то появляется непонятный шум! Особенно, когда света очень мало, на фотографиях по всей площади можно заметить характерные маленькие точки или отклонения яркости и цвета. Даже если мы сделаем снимок белого листа бумаги при плохом освещении, то получим такой грязный кадр:
Откуда берется эта грязь? И какое отношение к этому шуму имеет размер пикселя?
Этот мусор на матрицу приносят с собой фотоны. И дело совершенно не в том, что существуют нечистоплотные фотоны. Конечно нет. Всё дело в самой природе света.
Представьте, что на улице идет град и вы решили подсчитать, какое количество градин упадет в ведро за одну минуту. Чтобы увеличить точность эксперимента, вы решаете использовать сразу десять ведер. Итак, ведра расставлены — град идет. Проходит одна минута и вы делаете подсчет. Будет ли в каждом ведре одинаковое количество градин? Конечно же, нет! Любой человек ответит на этот вопрос и без каких-либо экспериментов.
Ровно то же происходит и с фотонами! Если какой-то пиксель за одну секунду поймал 100 фотонов, то в следующую секунду их могло легко оказаться 70, а может и 120. Добавьте к этому еще тот факт, что не каждый фотон будет поглощен в кремнии.
В общем, это ровно такое же непредсказуемое явление, как и пример с градом. Но если градины ни на что не влияют, то вот количество фотонов, упавших на пиксель, напрямую влияет на яркость этого пикселя на итоговом снимке.
Если бы у нас была матрица только с одним гигантским пикселем и мы делали снимок белой стены каждую секунду, на такой фотографии не было бы никакого шума, просто цвет стены каждый раз немного бы отличался. Собрали больше фотонов — снимок ярче, меньше фотонов — темнее.
Но у нас-то пикселей миллионы! И здесь происходит интересная вещь. Несмотря на то, что мы делаем снимок белой стены, на один пиксель может попасть 80 фотонов, на пиксель рядом — 120, а еще на другой — 100.
В итоге мы получаем вместо однородного белого цвета какие-то пятна, точки и прочие артефакты. Это и есть фотонный шум, связанный с самой природой света, который невозможно никак ни отследить, ни предугадать.
Конечно, существуют и другие источники шума, но этот — основной.
Помните, вначале я говорил, что мы подаем небольшое питание на кусочек кремния, чтобы он мог ловить фотоны и преобразовывать их в электроны? Так вот, когда ни один фотон не попадает на такой пиксель, слабый ток из-за небольшого нагрева кремния вызывает ровно тот же эффект — генерацию электронов, а матрица собирает их и считает, что это были фотоны. Но для того, чтобы этот шум был хоть как-то заметен, нужны длинные выдержки и мало света. На смартфонах длинные выдержки — большая редкость.
Кроме того, сам процесс считывания электронов может вносить шум. Но, опять-таки, он просто ничтожен в случае со смартфонами, так как смартфоны используют CMOS-сенсоры, а этот шум характерен для CCD-сенсоров (ниже я расскажу об этом чуть подробнее).
Так причем здесь размер пикселя?
Дело в том, что чем больше фотонов упадет на один пиксель, тем больше в нем появится электронов. А чем больше электронов, тем больше разница между шумом и реальной картиной. Когда мы говорим о шуме, нужно брать каждый пиксель, а не матрицу в целом.
Это очень просто понять даже интуитивно. Вот смотрите, если на все пиксели в среднем падает 9 фотонов, то мы можем легко посчитать уровень шума для всей матрицы. Согласно распределению Пуассона, шум — это просто квадратный корень из количества попавших на пиксель фотонов.
То есть, если в среднем пиксели ловят по 9 фотонов, значит шум всей матрицы — это квадратный корень из 9 или 3 фотона. На один пиксель упало 9 фотонов, на второй — 6, на третий — 10, на четвертый — 8 и так далее. Но в среднем, их количество отличается на +/- 3 фотона. Эта неравномерность и выльется в шум на снимке. И мы его прекрасно заметим, так как яркость точек на фотографии будет отличаться очень сильно (на 30% в среднем или на +/- 3 фотона на каждые 9 фотонов).
Но что произойдет, если пикселей будет в 4 раза меньше и они будут в 4 раза крупнее? Каждый пиксель будет собирать в среднем уже не по 9, а по 36 фотонов. И шум матрицы составит 6 фотонов (корень из 36).
Теперь разница в яркости между точками будет отличаться не более, чем на 16% (+/-6 фотонов на каждые 36 фотонов). Мы ничего, кроме размера пикселя, не изменили. Но фотография стала в 2 раза чище.
То есть, мы видим закономерность, что с увеличением количества фотонов, шум становится совершенно незначительным (относительно общего числа фотонов). Им можно пренебречь. Для 100 фотонов шум составит 10 фотонов. Если же увеличить количество фотонов в 100 раз, чтобы их было 10 тысяч, то шум возрастет только в 10 раз (корень из 10 тысяч = 100). И сигнал будет еще чище.
Получается, нам важно, чтобы как можно больше фотонов падало на один пиксель. Даже если на матрицу упало 1000 фотонов, лучше, чтобы пикселей было всего 10, тогда на каждый из них попадет в среднем по 100 фотонов. А если пикселей будет 100 (при том же размере матрицы), на каждый из них в среднем попадет по 10 фотонов. В первом случае шум будет едва заметен, так как яркость точек будет отличаться незначительно (+/- 10 фотонов на каждые 100 фотонов), а во втором случае — гораздо сильнее (+/- 3 фотона на каждые 10 фотонов).
Именно по этой причине большие пиксели меньше «шумят», чем маленькие (при одинаковом размере матрицы). У них соотношение сигнала (количества фотонов) к шуму (погрешности) гораздо выше.
И здесь я снова должен сказать «но»…
Но ведь у нас есть Quad Bayer и даже Nonacell!
Производители смартфонов нашли элегантное решение этой проблемы. Все современные матрицы смартфонов с размером пикселя 
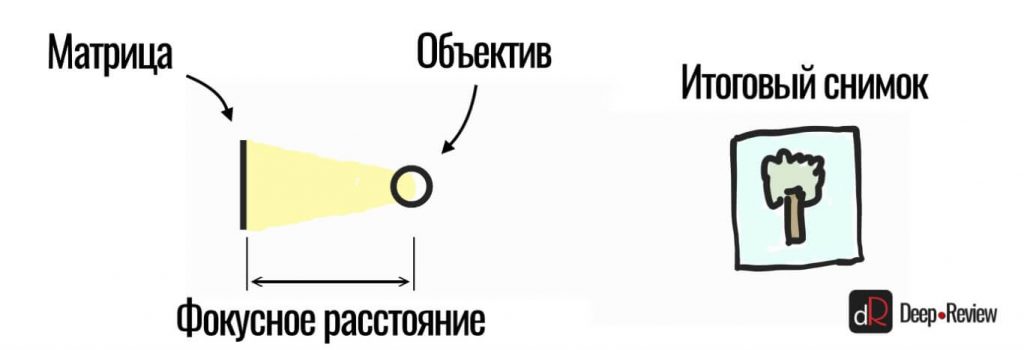
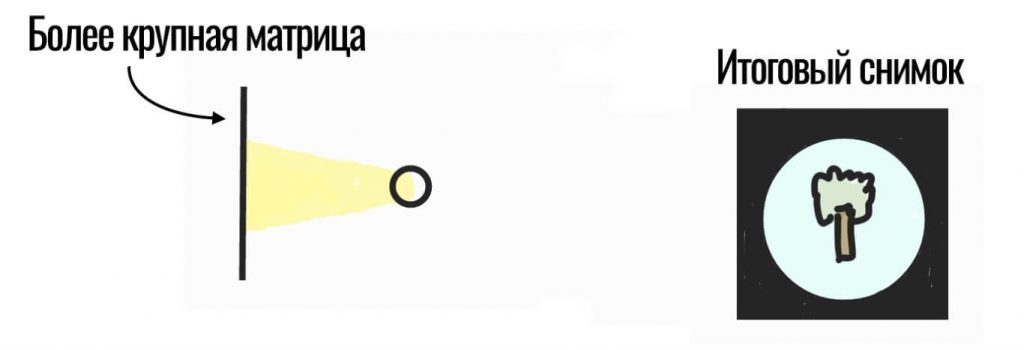
Что произойдет, если мы просто заменим маленькую матрицу на более крупную? На самом деле — ничего:
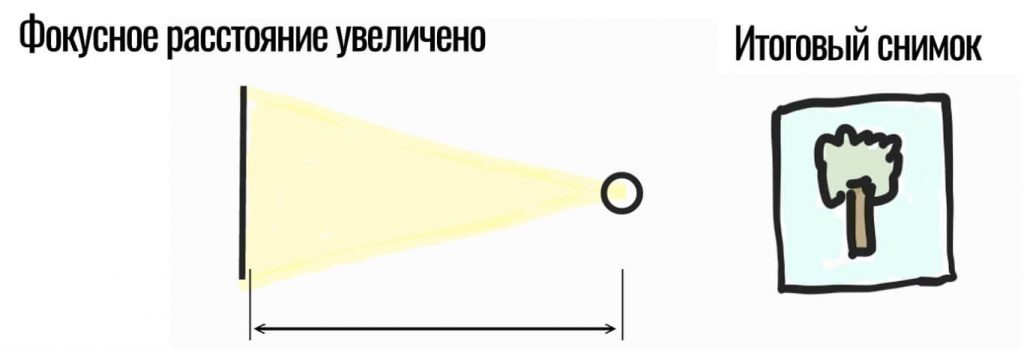
Мы будем получать фотографии с огромными черными рамками вокруг, так как линза проецирует такое же пятно света, как и раньше. Если мы хотим полностью задействовать весь сенсор, не меняя при этом угла обзора, нам нужно увеличить фокусное расстояние объектива, то есть, отодвинуть линзы подальше от сенсора:
Теперь фотоны падают на весь сенсор, а так как он гораздо крупнее, то и фотонов ловит больше. Верно? Нет, конечно.
Свет теперь покрывает весь сенсор, но интенсивность этого света упала (на картинке желтый цвет стал менее насыщенным), то есть, теперь на каждый условный квадратный миллиметр попадает меньше фотонов, чем раньше, так как нам пришлось заполнить тем же количеством фотонов большую площадь матрицы. Общее количество фотонов не возросло, так как диаметр отверстия остался прежним.
Это как фонарик: чем более узконаправленно он светит, тем ярче пятно света (выше интенсивность света).
Выходит, мы заменили маленький сенсор на большой, поставили другой объектив с более длинным фокусным расстоянием, но это никак не повлияло на качество снимков. Хотя кое-что уже изменилось в дизайне смартфона!
Так как нам пришлось увеличить фокусное расстояние, то есть, отодвинуть линзы подальше от сенсора, теперь объектив заметно выступает над корпусом. Вспомните Galaxy Note 20 Ultra:
Чтобы от всей проделанной нами работы был какой-то смысл, единственное, что еще остается сделать — это увеличить диаметр отверстия объектива. Вот теперь все звезды сошлись! В камеру попадает больше фотонов, интенсивность света увеличивается, а так как матрица крупная, то и каждый пиксель этой матрицы более крупный (или работает в режиме объединения пикселей), что приводит к более высокому качеству изображения.
Другими словами, сам по себе размер матрицы ничего не решает. Но именно с более крупными матрицами используют и объективы с большим диаметром отверстия, чтобы обеспечить соразмерное количество света. А это уже меняет всё.
Можно сделать такой вывод: если в смартфоне используется более крупная матрица, тогда диаметр входного зрачка объектива, скорее всего, также крупнее. Кроме того, выступ камеры над корпусом может косвенно свидетельствовать о том, что внутри установлен более крупный сенсор и компании пришлось отодвигать линзы подальше, чтобы компенсировать размер.
Неправильные дюймы. Или как узнать реальный размер матрицы в смартфоне?
Но как посчитать размер матрицы? Что означают цифры 1/2.55″ или 1/1.33″ в характеристиках смартфонов? Возможно, для кого-то это прозвучит странно, но такая маркировка используется производителями лишь по одной банальной причине — скрыть реальный размер матрицы, запутав пользователя.
Когда мы видим число с двойным штрихом, то понимаем, что это дюймы. А в одном дюйме — 25.4 мм. Если бы диагональ матрицы составляла 2″, мы бы легко перевели это в миллиметры, умножив 2 на 25.4 и получив 50.8 мм.
Было бы логичным предположить, что, если диагональ матрицы указана, как 1/1.33″, то нужно просто единицу разделить на 1.33, а потом умножить на 25.4 и мы получим диагональ в миллиметрах: 1 / 1.33 * 25.4 = 19 мм. Но в реальности матрица 1/1.33″ имеет диагональ 12 мм! Как же так?
Все дело в том, что производители используют не обычные дюймы, а видиконовские. Лет 70 назад были популярными телевизионные камеры с электронно-лучевыми трубками внутри. Работали они примерно, как и ЭЛТ-телевизоры. В трубке была маленькая мишень — аналог матрицы современного смартфона, и в эту матрицу выстреливались электроны.
Так вот, если диаметр трубки равнялся одному дюйму, то размер самой мишени («матрицы») внутри составлял 2/3 от диаметра трубки. Соответственно, в дюймовой трубке (25.4 мм) находилась мишень с диагональю 16.93 мм (25.4*2/3).
«Это же просто отличный способ маркировать современные прямоугольные матрицы!» — подумали производители и стали вместо человеческих миллиметров и дюймов использовать видиконовские дюймы, о которых еще помнят 10 человек, заставших 50-е годы прошлого столетия.
Получается, чтобы примерно высчитать диагональ матрицы в миллиметрах, нужно умножать полученное значение не на 25.4 мм (обычный дюйм), а на 16.93 (видиконовский дюйм). Теперь можно легко посчитать размер упомянутой выше матрицы: 1 / 1.33 * 16.93 = 12.7 мм.
Повторю еще раз. Когда вы видите в характеристиках смартфона размер матрицы, скажем, 1/3.2″, нужно просто единицу разделить на 3.2, а затем полученное число умножить на 16.93. Вот вам и диагональ в привычных миллиметрах!
Делаем выводы
Качество камер современных смартфонов возросло очень сильно при том, что размеры одного пикселя продолжают уменьшаться. Так что, маленький пиксель — это не приговор.
Производители постоянно работают над тем, чтобы как можно больше фотонов попадало на один пиксель. Для этого улучшаются материалы цветных фильтров и линз, чтобы они блокировали как можно меньше света. Внутри одного пикселя сокращаются размеры транзисторов и увеличивается площадь светочувствительного элемента (того самого кусочка кремния).
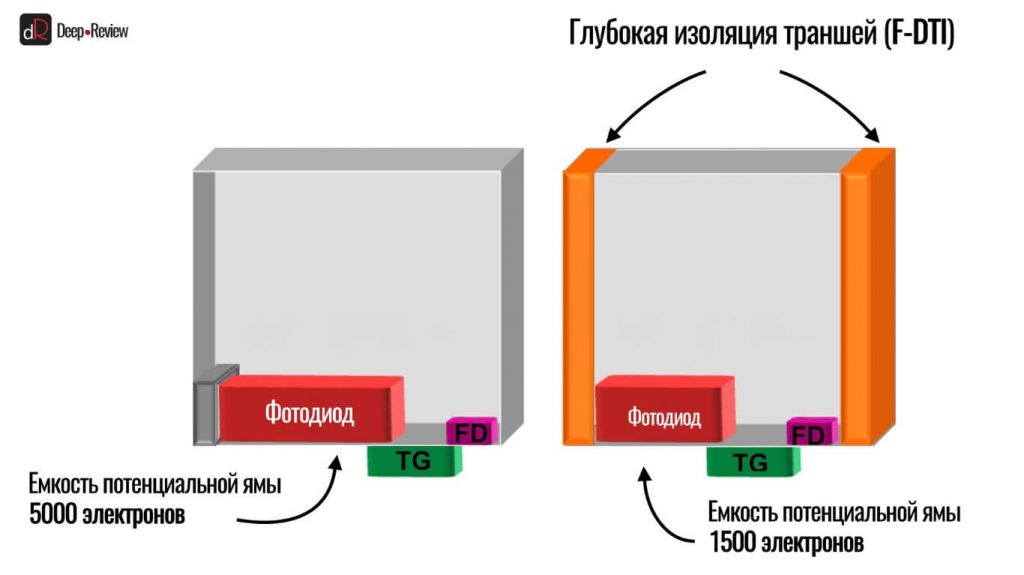
Новые технологии изоляции пикселей (DTI и F-DTI) позволили значительно сократить их размеры без ущерба качеству, а ведь раньше это приводило к тому, что электроны из одного пикселя могли спокойно перескакивать на соседние:
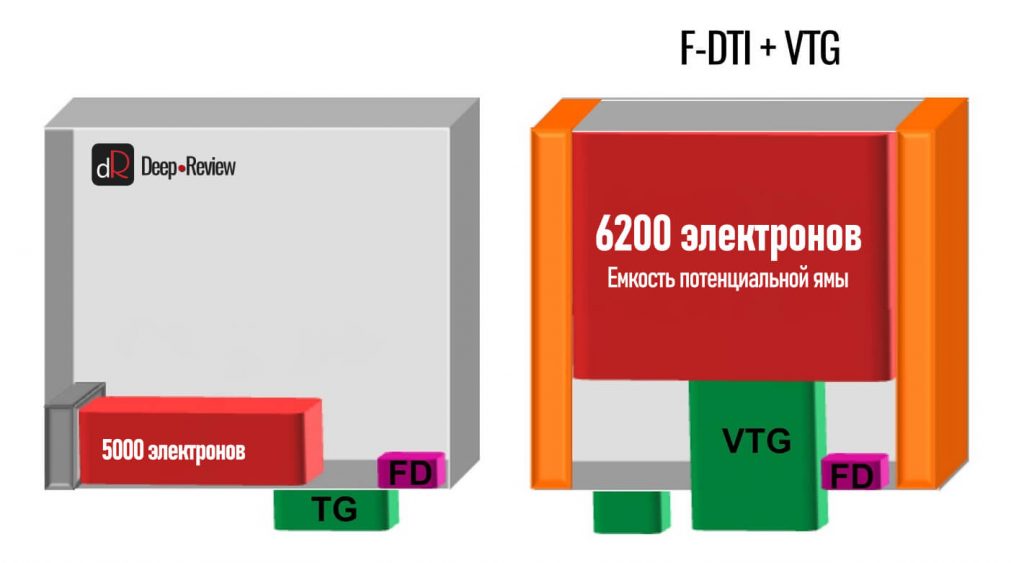
Но, как вы заметили, с уменьшением пикселя, уменьшался и светочувствительный элемент, а значит и емкость его потенциальной ямы. Эту проблему решили другие технологии, в частности VTG (Vertical Transfer Gate), которая позволила размещать фотодиод внутри пикселя над другими компонентами, а не рядом с ними:
В итоге, пиксель всё уменьшался, а его светосила — увеличивалась.
И в этой связи довольно забавно читать, как многие люди на форумах с грустью вспоминают старые-добрые времена, когда пиксели в смартфонах еще были большими, а не то, что эти модные 0.8 мкм.
Но в действительности, современные маленькие пиксели захватывают больше света, чем старые крупные, так как технологии с тех пор очень сильно ушли вперед и матрицы стали намного качественнее именно с точки зрения физики. Не говоря уже об алгоритмах, нейросетях и машинном обучении.
20 лет назад все говорили, что невозможно нарушить законы физики и телефоны никогда не смогут заменить фотоаппарат. Но проблема оказалась не в законах физики, а в несовершенстве технологий. Физика со своими законами осталась там же, где и была 20 или 2000 лет назад, но технологии продолжают показывать экспоненциальный рост, о чем, собственно, у меня есть отдельная интересная статья…
Позвольте еще раз привести характеристики камеры случайно выбранного смартфона:
Теперь все эти цифры и буквы не должны вас пугать, так как мы подробно разобрались буквально с каждым параметром, за исключением PDAF и OIS. Но об этом поговорим в другой раз!
Алексей, глав. редактор Deep-Review
P.S. Не забудьте подписаться в Telegram на первый научно-популярный сайт о мобильных технологиях — Deep-Review, чтобы не пропустить очень интересные материалы, которые мы сейчас готовим!
Как бы вы оценили эту статью?
Нажмите на звездочку для оценки
Внизу страницы есть комментарии.
Напишите свое мнение там, чтобы его увидели все читатели!
Если Вы хотите только поставить оценку, укажите, что именно не так?