как узнать результирующую силу

Второй закон Ньютона

С точки зрения физики правильнее выражать второй закон Ньютона следует так:

Такая формулировка гораздо более понятна.

Единицы измерения силы

В системе СИ:
ΣF = кг·м/с 2 = ньютон (Н)

В системе СГС:
ΣF = г·см/с 2 = дина

Результирующая сила

Для получения результирующей силы-вектора необходимо сложить все силы-векторы, действующие на тело.

Если дело обстояло именно так, то воз вряд ли будет покоиться на месте.

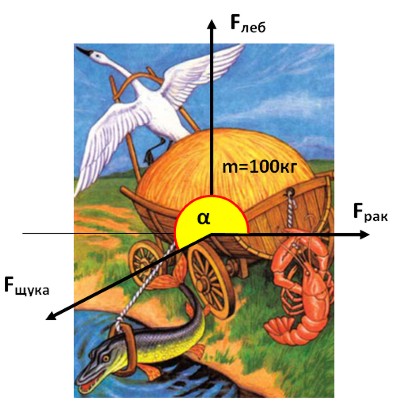
Предположим, что на воз, массой 100 кг действуют силы, указанные на рисунке:

Fлеб = 150 Н; Fрак = 125 Н; Fщука = 65 Н; α = 210°

Давайте попытаемся определить местоположение воза через 10 секунд. Для этого надо:

I. Ищем результирующую силу

Находим составляющие векторов. Для первых двух сил это просто (т.к. они направлены по осям X и Y):

Fлеб = (0;150Н); Fрак = (125Н;0)

Для щуки немного сложнее:

Fщука = (Fщ_x;Fщ_y) = (Fщ·cosα;Fщ·sinα) = (65·cos210°;65·sin210°) = (65·(-0,87);65·(-0,5)) = (-57Н;-33Н)

Теперь складываем вектора:

Мы нашли не только величину результирующей силы, но и ее направление!

II. Определяем ускорение

a = ΣF/m = (68Н;116Н)/100кг = (0,68м/с 2 ;1,18м/с 2 )

III. Находим расстояние

Но, поскольку изначально воз стоял на месте:

S = 1/2a(t₁) 2 = 1/2(0,68м/с 2 ;1,18м/с 2 )·(10) 2 = (34м;59м)

Таким образом, можно утверждать, что через 10 секунд после того, как Лебедь, Рак и Щука начнут тянуть воз (согласно нашей диаграмме), он переместится на расстояние 34 метра вдоль оси X и на 59 метров вдоль оси Y.

Попробуйте самостоятельно решить обратную задачу:

Какую силу необходимо приложить к автомобилю весом 1 тонна, чтобы разогнать его с места до 100 км/ч за 10 секунд? Трением можно пренебречь.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Источник

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Разложение вектора силы по направлениям

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Модуль равнодействующей определим с помощью теоремы Пифагора:

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Дано:

F 1 → = F t g β ≈ 577 Н ;

Источник

Формула силы

Определение и формула силы

Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень» (интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.

Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.

Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.

Второй закон Ньютона

Равнодействующая всех сил приложенных к телу (векторная сумма всех сил) ($\bar$) равна производной от импульса тела по времени:

Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней (второй закон Ньютона) можно представить в виде:

Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:

Единицы измерения силы

Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с 2

Примеры решения задач

Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:

Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения. Для этого найдем производные по времени от соответствующих координат:

Так как модуль ускорения равен:

то, учитывая выражения (1.2) и (1.3), получаем:

Так как a_y=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение и силы совпадают, а мы получили:

Исходя из второго закона Ньютона, имеем:

$$F=m \cdot 6 \alpha t, \bar=m 6 \alpha t \cdot \bar$$

Формула силы не по зубам? Тебе ответит эксперт через 10 минут!

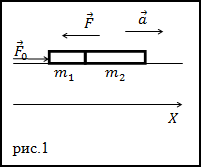
Решение. Сделаем рисунок.

Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:

В проекции на ось Xуравнение (2.1) примет вид:

$$F_<0>-F=m_ <1>a \rightarrow F=F_<0>-m_ <1>a(2.2)$$

Рассмотрим силы, приложенные к двум параллелепипедам как системе:

В проекции на ось X уравнение (2.3) примет вид:

Из уравнения (2.4) выразим ускорение:

Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:

Источник

Результирующая сила: как она рассчитывается и решаются упражнения

Содержание:

В прочность в результате это сумма всех сил, действующих на одно и то же тело. Когда на тело или объект действует одновременно несколько сил, возникает эффект. Действующие силы можно заменить одной силой, которая производит такой же эффект. Эта единственная сила является результирующей силой, также известной как чистая сила, и обозначается символом F_р.

Эффект, который он производит F_рэто будет зависеть от его размера, направления и смысла. Физические величины, имеющие направление и смысл, являются векторными величинами.

Как силы, действующие на вектор тела, равнодействующая сила F_р это векторная сумма всех сил, которую можно графически представить стрелкой, указывающей ее направление и направление.

С помощью равнодействующей силы проблема тела, на которое действует несколько сил, упрощается, сводя ее к единственной действующей силе.

Формула

F_р= Результирующая сила

∑F = Сумма сил

Результирующая сила также может быть представлена ​​уравнением второго закона Ньютона.

а = ускорение тела

Если уравнение (1) подставить в уравнение (3), будут получены следующие уравнения:

∑F = м.к (4)

Математические выражения (4) и (5) предоставляют информацию о состоянии тела, получая вектор ускорения к.

Как рассчитывается результирующая сила?

Результирующая сила получается путем применения Второго закона Ньютона, который гласит следующее:

Чистая сила, действующая на тело, равна произведению его массы и ускорения, которое оно приобретает.. (Уравнение (3))

Ускорение тела будет иметь направление приложенной чистой силы. Если все силы, действующие на тело, известны, достаточно добавить их векторно, чтобы получить результирующую силу. Точно так же, если известна равнодействующая сила, достаточно разделить ее на массу тела, чтобы получить его ускорение.

Если результирующая сила равна нулю, тело находится в состоянии покоя или с постоянной скоростью. Если на тело действует одна сила, результирующая сила равна этой силе F_р=F.

Когда несколько сил действуют на одно и то же тело, необходимо учитывать компоненты вектора силы, независимо от того, параллельны ли эти силы или нет.

Если сила, приложенная к книге, имеет наклон по отношению к горизонтальной плоскости стола, сила записывается как функция вертикальной и горизонтальной составляющих.

Результат параллельные силы

Когда силы, действующие на тело, имеют одинаковое направление и одинаковое направление или имеют противоположное направление, результирующая сила получается путем выполнения алгебраической суммы численных значений сил.

Непараллельные силы

Когда к телу прилагаются непараллельные силы, равнодействующая сил будет иметь прямоугольную и вертикальную составляющие. Математическое выражение для расчета чистой силы:

∑ F_Икс и ∑ F_Икс= Алгебраическое суммирование компонентов Икс а также Y приложенных сил

θ_Икс= угол, образованный равнодействующей силой F_р с валом Икс

Обратите внимание, что результирующая сила выражения (6) не выделена жирным шрифтом, потому что она выражает только числовое значение. Направление определяется углом θ_Икс.

Выражение (6) справедливо для сил, действующих в одной плоскости. При действии сил в пространстве учитывается составляющая z силы, если вы работаете с прямоугольными компонентами.

Решенные упражнения

Параллельные силы одного направления складываются и вычитаются с параллельной силой противоположного направления.

Результирующая сила имеет величину 78 Н в горизонтальном направлении.

2. Вычислить равнодействующую силу тела под действием двух сил. F_{1 Y} F₂. Сила F₁ он имеет магнитуду 70 Н и наносится горизонтально. Сила F₂ он имеет магнитуду 40 Н и применяется под углом 30 ° к горизонтальной плоскости.

Для решения этого упражнения строится диаграмма свободного тела с осями координат. Икс а также Y

Все компоненты определены Икс а также Y сил, действующих на тело. Сила F₁ имеет только одну горизонтальную составляющую на оси Икс. Сила F₂он состоит из двух компонентов F_2xи F_{2 и} которые получаются из функций синуса и косинуса угла 30 °.

После определения результирующих сил на валу Икс а также Y переходим к получению численного значения равнодействующей силы.

Угол, образованный равнодействующей силой F_р получается из следующего выражения:

Результирующая сила F_р он имеет звездную величину 106,53N и имеет направление, определяемое углом 10,82 °, который он образует с горизонтом.

Ссылки

Экспериментальная психология: ее 5 направлений и целей

Источник

Принцип суперпозиции сил и полей

теория по физике 🧲 электростатика

Принцип суперпозиции сил

Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:

F_i— сила, с которой электрическое поле зарядом q действует на пробный заряд q_i, помещенный в это поле на расстоянии r_iот этого заряда. Численно ее можно вычислить по формуле:

Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):

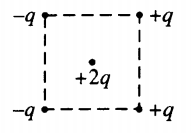
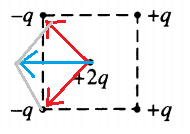
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.

Принцип суперпозиции полей

Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:

− E i — напряженность, создаваемая зарядом q i в точке, находящейся на расстоянии r i :

Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:

φ i — потенциал электростатического поля, создаваемого зарядом q i на расстоянии r i от него. Численно он равен:

Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:

Примеры определения расстояний

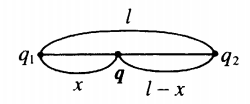Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними:

Изучаемый заряд лежит в вершине квадрата со стороной a:

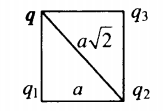
r 1 = r 3 = a ; r 2 = a √ 2

Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:

Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:

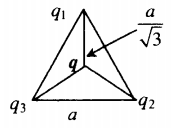
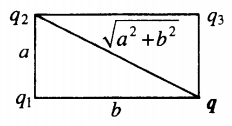
r 1 = b ; r 2 = √ a 2 + b 2 ; r 3 = a

Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120 о :

Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:

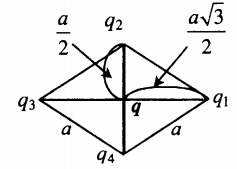
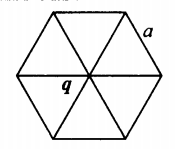
r 1 = r 2 = r 3 = r 4 = r 5 = r 6 = a

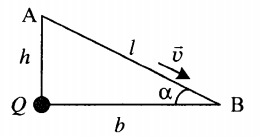
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.

Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):

Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:

В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:

Расстояние между точкой В и местом, где находится заряд Q:

Приравняем правые части уравнений:

Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?

Источник