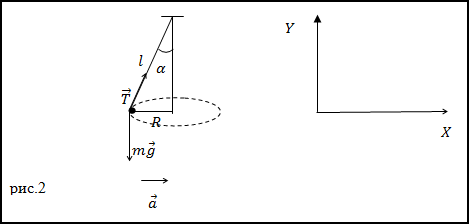как узнать силу натяжения

Сила натяжения нити

Понятие силы натяжения нити

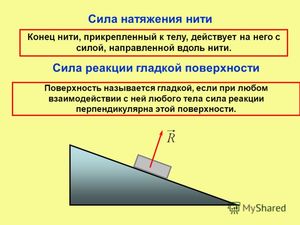
Сила натяжения нити является реакцией подвеса (нити), на действие со стороны тела на подвес. Сила натяжения нити всегда имеет направление вдоль нити.

Очень часто при решении задач указывают, что нить является невесомой (массой нити в сравнении с массой груза можно пренебречь). Если нить невесома и нерастяжима, то такую нить рассматривают как проводник силы.

Если следует учитывать растяжение нити, при этом нагрузки малы, а нить упругая, то при вычислении силы натяжения используют закон Гука:

Единицей измерения силы натяжения нити в Международной системе единиц (СИ) (как и для любой другой силы) является ньютон:

Примеры задач на силу натяжения нити

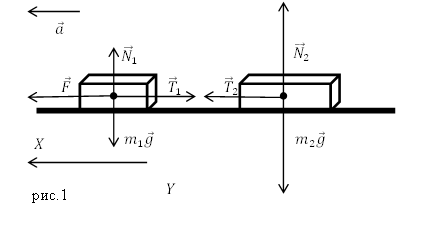
Решение. Рассмотрим силы, которые приложены к первому грузу, запишем второй закон Ньютона для этого тела:

Проектируя на оси X и Y уравнение (1.1) получаем:

\[\left\< \begin X:F-T_1=m_1a\left(1.2\right). \\ m_1g=N_1\left(1.3\right). \end \right.\]

Рассмотрим силы, действующие на второй груз, запишем второй закон Ньютона для этих сил:

В проекциях на оси X и Y получаем систему уравнений:

\[\left\< \begin X:T_2=m_2a\left(1.5\right). \\ m_2g=N_2\left(1.6\right). \end \right.\]

Так как нить считаем невесомой, то имеем:

Из уравнения (1.5) выразим ускорение и подставим его в (1.2)получим величину силы натяжения нити:

Задание. К нерастяжимой нити подвешен массивный шарик. Шарик подняли так, что нить приняла горизонтальное положение, затем шарик отпустили. Какова сила натяжения нити в момент, когда шарик проходит положение равновесия? Какой угол составляет нить с вертикалью, если сила натяжения равна силе тяжести, действующая на шарик?

Решение. Сделаем рисунок.

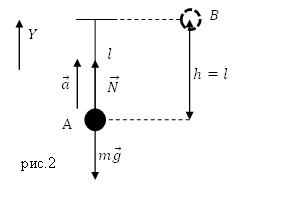
1) Силы, действующие на шарик в момент прохождения положения равновесия (положение А на рис.2): сила тяжести и сила натяжения нити. Для них запишем второй закон Ньютона:

Запишем проекцию выражения (2.1) на ось Y:

где шарик движется с центростремительным ускорением, равным:

Выразим силу натяжения нити из (2.2), подставим найденное ускорение, учитывая (2.4):

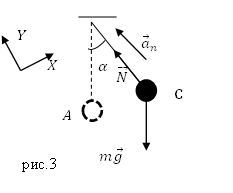
Ось Y направим по нити, ось X перпендикулярно оси Y (рис.3).

Запишем проекцию уравнения (2.1) на новую ось Y:

Выразим силу натяжения нити:

Учитывая (2.3), получим:

Подставим результат (2.9) в формулу (2.7), получили:

Приравниваем по условию силу натяжения нити к силе тяжести, выражаем величину угла:

Источник

Сила натяжения нити и применение формулы в бытовых ситуациях

Силой натяжения называют ту, что действует на объект, сравнимый с проволокой, шнуром, кабелем, ниткой и так далее. Это могут быть несколько объектов сразу, в таком случае сила натяжения будет действовать на них и необязательно равномерно. Объектом натяжения называют любой предмет, подвешенный на все вышеперечисленное. Но кому это нужно знать? Несмотря на специфичность информации, она может пригодиться даже в бытовых ситуациях.

Например, при ремонте дома или квартиры. Ну и, конечно же, всем людям, чья профессия связана с расчетами:

Натяжения нити и подобных объектов

А зачем им это знать и какая от этого практическая польза? В случае с инженерами и конструкторами знания о мощи натяжения позволят создавать устойчивые конструкции. Это означает, что сооружения, техника и прочие конструкции смогут дольше сохранять свою целостность и прочность. Условно, эти расчеты и знания можно разделить на 5 основных пунктов, чтобы в полной мере понять, о чем идет речь.

1 Этап

Задача: определить силу натяжения на каждом из концов нити. Эту ситуацию можно рассматривать как результат воздействия сил на каждый конец нити. Она равняется массе, помноженной на ускорение свободного падения. Предположим, что нить натянута туго. Тогда любые воздействия на объект приведет к изменению натяжения (в самой нити). Но даже при отсутствии активных действий, по умолчанию будет действовать сила притяжения. Итак, подставим формулу: Т=м*g+м*а, где g – ускорение падения (в данном случае подвешенного объекта), а – любое иное ускорение, действующее извне.

Есть множество сторонних факторов, влияющих на расчеты – вес нити, ее кривизна и так далее. Для простых расчетов это мы не будем пока что учитывать. Иными словами – пусть нить будет идеальна с математической точки зрения и «без изъянов».

Возьмем «живой» пример. На балке подвешена прочная нить с грузом в 2 кг. При этом отсутствует ветер, покачивания и прочие факторы, так или иначе влияющие на наши расчеты. Тогда мощь натяжения равна силе тяжести. В формуле это можно выразить так: Fн=Fт=м*g, в нашем случае это 9,8*2=19,6 ньютона.

2 Этап

Заключается он в вопросе об ускорении. К уже имеющейся ситуации давайте добавим условие. Суть его в том, чтобы на нить действовало еще и ускорение. Возьмем пример попроще. Представим, что нашу балку теперь поднимают вверх со скоростью 3 м/с. Тогда, к натяжению прибавится ускорение груза и формула примет следующий вид: Fн=Fт+уск*м. Ориентируясь на прошлые расчеты получаем: Fн=19,6+3*2=25,6 ньютона.

3 Этап

Тут уже посложнее, так как речь идет об угловом вращении. Следует понимать, что при вращении объекта вертикально, сила, воздействующая на нить, будет намного больше в нижней точке. Но давайте возьмем пример с несколько меньшей амплитудой качания (по типу маятника). В этом случае для расчетов нужна формула: Fц=м* v²/r. Тут искомое значение обозначает дополнительную мощь натяжения, v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз. Последнее значение фактически равняется длине нити, пускай она составляет 1,7 метра.

Итак, подставляя значения, находим центробежные данные: Fц=2*9/1,7=10,59 ньютона. А теперь, чтобы узнать полную силу натяжения нити, надо к имеющимся данным о состоянии покоя прибавить центробежную силу: 19,6+10,59=30,19 ньютона.

4 Этап

Следует учитывать меняющуюся силу натяжения по мере прохождения груза через дугу. Иными словами – независимо от постоянной величины притяжения, центробежная (результирующая) сила меняется по мере того, как качается подвешенный груз.

Чтобы лучше понять этот аспект, достаточно представить себе привязанный груз к веревке, которую можно свободно вращать вокруг балки, к которой она закреплена (как качели). Если веревку раскачать достаточно сильно, то в момент нахождения в верхнем положении сила притяжения будет действовать в «обратную» сторону относительно силы натяжения веревки. Иными словами – груз станет «легче», из-за чего ослабнет и натяжение на веревку.

Предположим, что маятник отклоняется на угол, равный двадцати градусам от вертикали и движется со скоростью 1,7 м/с. Сила притяжения (Fп) при этих параметрах будет равна 19,6*cos(20)=19,6*0,94=18,424 Н; центробежная сила (F ц=mv²/r)=2*1,7²/1,7=3,4 Н; ну а полное натяжение (Fпн) будет равняться Fп+ Fц=3,4+18,424=21,824 Н.

5 Этап

Его суть заключается в силе трения между грузом и другим объектом, что в совокупности косвенно влияет на натяжение веревки. Иначе говоря – сила трения способствует увеличению силы натяжения. Это хорошо видно на примере перемещения объектов по шершавой и гладкой поверхностях. В первом случае трение будет большим, поэтому и сдвигать предмет становится тяжелее.

Общее натяжение в данном случае вычисляется по формуле: Fн=Fтр+Fу, где Fтр – трение, а Fу – ускорение. Fтр=мкР, где мк – трение между объектами, а Р – сила взаимодействия между ними.

Чтобы лучше понять данный аспект, рассмотрим задачу. Допустим, у нас груз 2 кг и коэффициент трения равен 0,7 с ускорением движения 4м/с постоянной скорости. Теперь задействуем все формулы и получаем:

Теперь вы знаете больше и можете сами находить и рассчитывать нужные значения. Конечно, для более точных расчетов нужно учитывать больше факторов, но для сдачи курсовой и реферата этих данных вполне достаточно.

Видео

Это видео поможет вам лучше разобраться в данной теме и запомнить ее.

Источник

Определение силы натяжения нити

Сила натяжения нити — формулировка

Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

Как определить силу, формулы

Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

С неподвижно закрепленным верхним концом

Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:

где m – это масса тела, а g представляет собой ускорение свободного падения.

Если нить под углом

В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.

где а равен углу отклонения.

Формула с учетом ускорения и массы

В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:

Сила натяжения во вращающейся системе

Описание

Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:

Формула расчета

Рассчитать силу натяжения в условиях вращающейся системы можно так:

Обозначение, единица измерения

Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)

Примеры решения задач

Задание 1

На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.

Решение

Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.

\(\bar\) является силой натяжения нити.

Проекция уравнения будет иметь следующий вид:

Данное выражение позволяет рассчитать ускорение:

Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления

Задание 2

На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.

Решение

Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:

Проекции данной формулы по осям определяются следующим образом:

X: \(T sin α = ma = mω2R\)

Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:

Анализ рисунка позволяет вывести следующее уравнение:

\(\sin \alpha = \frac\rightarrow \cos \alpha = \sqrt<1-\left(\frac \right)^<2>>\)

Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:

Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:

Источник

Формула силы натяжения нити

Определение и формула силы натяжения нити

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

Примеры решения задач

Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

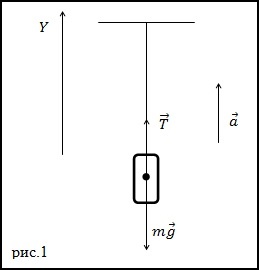
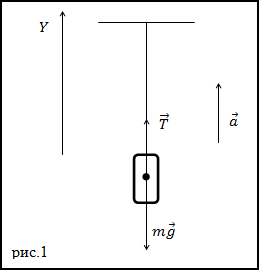
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

Из выражения (1.2) получим ускорение:

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

Ответ. a=1,2м/с 2

Формула силы натяжения нити не по зубам? Тебе ответит эксперт через 10 минут!

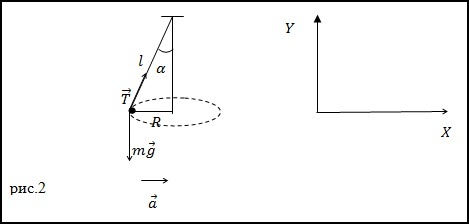
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

$$ \begin X: \quad T \sin \alpha=m a=m \omega^ <2>R(2.2) \\ Y: \quad-m g+T \cos \alpha=0 \end $$

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

Источник

Формула силы натяжения нити в физике

Сила натяжения нити: определение☑️, формулы для расчета силы в разных условиях⚠️, обозначение. Куда направлена, примеры решения задач

Определение и формула силы натяжения нити

Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.

Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:

Об этой статье

Эту страницу просматривали 239 261 раз.

Сила натяжения нити — формулировка

Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

Примеры решения задач по теме «Сила натяжения нити»

Силы в механике

1. Сила тяжести.

На любое тело, находящееся вблизи поверхности земли или лежащее на земле действует сила, равная произведению массы тела на ускорение свободного падения:.

2. Сила реакции опоры (нормальной реакции, упругости опоры)

Сила, действующая о стороны опоры на лежащее на ней тело. Всегда направлена перпендикулярно поверхности соприкосновения тела и опоры.

vec –сила реакции опоры.

Если тело лежит на внутренней поверхности сферы, сила vec направлена к центру сферы.

Если тело лежит на внешней поверхности сферы, сила vec направлена от центра сферы.

3. Сила натяжения нити

Сила, действующая со стороны нити (веревки, каната, троса, стержня и т.п.) на тело, которое висит на нити (веревке и т.п.). Направлена вдоль нити (и т.п.).

vec–Сила натяжения нити.

4. Вес тела

Определение: – это сила, с которой тело давит на опору или растягивает подвес.

Вес тела равен по модулю силе реакции опоры или силе натяжения нити, направлен в противоположную сторону и приложен к другому телу: либо опоре, либо нити.

vec –сила реакции опоры;

5. Сила трения

a) Сила трения скольжения

Сила трения скольжения направлена противоположно относительной скорости тел и не зависит от площади соприкосновения поверхностей.

vec_ <тр>–сила трения скольжения.

Модуль силы трения равен произведению коэффициента трения скольжения на модуль силы реакции опоры:

mu –коэффициент трения скольжения.

b) Сила трения качения

Действует на тело, которое не скользит, а катится по некоторой поверхности.

vec_ <тр>–сила трения качения.

mu _ <1>–коэффициент трения качения.

Коэффициент трения качения много меньше коэффициента трения скольжения

c) Сила трения покоя

Действует на тело, лежащее неподвижно на некоторой поверхности, которое мы пытаемся сдвинуть с места. Противоположно направлена внешней силе и равна ей по модулю.

vec_ <тр.п.>– сила трения покоя.

vec_ <внешн.>– внешняя сила.

6. Схема решения задач

a) Нарисовать все силы, приложенные ко всем телам системы;

b) Выбрать системы отсчета (можно свою для каждого тела);

c) Спроектировать силы на оси;

d) Записать уравнения для второго закона Ньютона в проекциях для всех тел системы;

e) Записать кинематические связи, то есть связи между скоростями и ускорениями различных тел системы;

f) Решить полученную систему уравнений.

Механизм образования поверхностного натяжения

В основе природы сил поверхностного натяжения лежит электростатическое притяжение молекул, находящихся на близком расстоянии в жидкости.

В самом деле, в жидкости, в отличие от газа, силы притяжения между молекулами больше, чем силы отталкивания, и энергия этого притяжения больше тепловой энергии, стремящейся распределить молекулы как можно шире. Поэтому равнодействующая сил, действующая на отдельную молекулу, будет направлена в сторону геометрического центра тела, образованного остальными молекулами.

В результате из-за отсутствия других сил молекулы жидкости всегда собираются в шарообразное тело. Равнодействующая сил, действующих на молекулы в глубине этого тела, практически равна нулю. Равнодействующая сил, действующая на молекулы на границе тела, направлена в сторону центра. Это приводит к тому, что плотность молекул внутри жидкости больше, чем плотность молекул, находящихся на границе. В результате в поверхностном слое возникают силы, стремящиеся к сокращению площади поверхности, — это и есть сила поверхностного натяжения.

Рис. 1. Силы, действующие на молекулы поверхности жидкости.

Проявления [ править | править код ]

Водомерка на поверхности воды.

Так как увеличение площади поверхности раздела жидкость — газ требует совершения работы, жидкость «стремится» уменьшить площадь своей поверхности:

Единицы измерения силы натяжения нити

Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н

Силы упругости: пружины, канаты и нити

В задачах в этой статьи рассмотрены случаи, когда тело поднимают или опускают с ускорением. При этом натяжение нити, на которой подвешен груз, разное. Даны примеры составления уравнений по второму закону Ньютона в проекциях на оси.

Задача 1. Грузовик взял на буксир легковой автомобиль массой т и, двигаясь равноускоренно, за с проехал м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость Н/м? Трение не учитывать.

Удлинение троса можно найти, зная силу упругости:

Так как трение учитывать не нужно, то по второму закону Ньютона

Определим ускорение грузовика:

Окончательно для удлинения троса получаем:

Ответ получен в метрах, можно записать его в мм: 0,64 мм.

Задача 2. На нити, выдерживающей натяжение Н, поднимают груз массой кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту , на которую можно поднять груз за с так, чтобы нить не оборвалась.

Запишем второй закон Ньютона в проекция на вертикальную ось:

Тогда ускорение равно:

Высота, на которую тело можно поднять с таким ускорением, равна

Задача 3. Веревка выдерживает груз массой кг при вертикальном подъеме его с некоторым ускорением и груз массой кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза , который можно поднимать или опускать на этой веревке с постоянной скоростью?

Запишем уравнения по второму закону как для подъема, так и для спуска тела. Направим ось вверх, тогда при подъеме:

Ускорение по условию одно и то же, тогда:

Приравняв, можем найти силу натяжения веревки, которую она выдерживает:

Если бы груз массой просто висел на такой веревке, то мы бы записали

Задача 4. Груз массой кг подвешен к пружине жесткостью Н/м. Длина пружины в нерастянутом состоянии м. Найти длину пружины , когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением м/с, направленным а) вверх; б) вниз?

Если груз повешен на пружину, ее длина увеличивается:

При движении лифта вверх запишем второй закон (ось направлена вверх):

Тогда длина пружины в этом случае:

При движении лифта вниз запишем второй закон (ось направлена вверх):

Тогда длина пружины в этом случае:

Ответ: , , .

Задача 5. Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно и , а вертикальных – и . С каким ускорением движется тележка по горизонтальной плоскости?

Запишем уравнения по второму закону в проекциях на оси, которые расположим традиционно: ось вправо, ось – вверх. Тогда, если тележка движется вправо, по оси, имеем:

Из второго уравнения найдем массу груза:

Тогда ускорение тележки (и груза) равно:

Если же тележка движется влево (против оси), то изменится только первое уравнение:

Тогда ускорение тележки (и груза) равно:

Как настроить натяжение нижней нитки в швейной машине

Обещанный ортдельный пост. Как настроить натяжение нижней (!) нити в швейной машине.Все любят крутить колесо натяжения верхней нити, однако в свое время мастер меня научил, что начинается идеальный шов не с этого! А с правильного натяжения нижней нити. Почему-то многие очень боятся крутить челнок, в котором шпулька. При этом главный аргумент: “Там винтик маленький, боюсь, что он упадет, и я его больше никогда не найду”. Не вижу в этом драмы – уж насколько я слепая, а винтик этот нахожу всегда. В основном по звуку, слышу, куда он упал. Если у вас в закрытом помещении что-то важное упало, куда оно денется – обыщете ближайший метр и найдете. Не говоря уж о том, что это вообще большая редкость, что такой винт вываливается, и если вы так боитесь, работайте над столом и над листом белой бумажки. Точно не промахнетесь.

Так вот – винт этот нужно крутить на самом деле, очень и очень мало. Минимально! На какой-то малюсенький кусочек градуса! Т.е. с чувством и без фанатизма. Если так крутить, он и вываливаться не будет.

В общем, вкладываем в челнок шпульку. На этом месте уже начинается одна из самых яростных дискуссий – в какую сторону ниткой вкладывать шпульку? В какую сторону оно долно отматываться? Вот это “отматываться по часовой стралке”, это вообще капец. Бесконечная дискуссия – что должно крутиться по часовой стрелке? Ника? Шпулька?

Итак, берете шпульку так, чтобы нитка свисала с правой стороны. Вот так.

И на эту шпульку, вот так держанную, как бы надеваете челнок. Закрытой частью к себе, открытой – от себя. Тогда будет правильно.

Теперь беремся за нитку, вот так:

И смотрим, что происходит. Если челнок повис на нитке без движения, и от встряхивания остается на том же месте, значит натяжение слишком сильное. Если все это несется с большой скоростью вниз – слишком слабое. Начинаем крутить винт (подходящей отверткой). А у кого на челноке два винтика (модели постарше), те крутят их примерно поровну, один, потом другой. Капельку (совсем капельку!) подкрутили, и пробуем еще.

Идеальный результат выглядит так: вы беретесь за нитку, и челнок для начала на ней повисает. Но если вы слегка встряхиваете все это, он отматывается вниз где-то на 5-10 см, потом тормозит и останавливается. Если он просто летит вниз – мало. Если он сантиметров через 10 *почти* остановился, но после тормсожения еще продолжает медленно ползти вниз – мало. Если оно именно скатилось на какой-то такой кусок, и потом остановилось и стоит – хорошо! Если вы его встряхнули, а оно опустилось вниз всего на пару см, и резкоим движением тормознуло – много. Если оно спускается два-три раза очень небольшими рывками, потом останавливается, но в целом пролетело меньше 5 см – все еще многовато.

Вот когда стало “как надо” вставляем челнок в машину, и начинаем заниматься верхней частью.

Внимание: если вы беретесь шить другим сортом нитки (например, у вас была Х/Б нитка, а потом вы решили пошить синтетической, которая более гладкая и тоньше), надо все перенастраивать. Наверняка при смене нитки окажется, что натяжения стало сильно мало. (Хлопчатые “мохнатые” нитки гораздо больше тормозят).

И еще: пока вы вот так пробуете, у вас куча нитки отмотается. Иногда нужно штук 10 попыток, пока натяжение не станет хорошим. Многим почему-то жалко этого метра нитки, который они при этом отматывают. Мол, пропал. А то что вы миллион метров нехорошего шва сошьете, испортив и нитки, и ткань, и нервы – это не жалко?

Теперь заправляем машину и шьем. Смотрим на шов, который получился. Вот прекрасная картинка нашлась в интернете, которая показывает, чего мы добиваемся. Нитки, верхняя и нижняя, встречаются и переплетаются где-то между слоями ткани. Так вот, нужно добиться того, чтобы место их встречи было по возможности посередине между слоями ткани. А не ближе к одной из поверхностей.

Понятно, что толщины там мало. И мы говорим о каких-то десятых миллиметра. Но это можно настроить, чтобы было действительно точно в середине.

Хороший шов, это когда стежки ложатся рядом, строчка ровная, но (!) при этом видно каждый отдельный стежок. Т.е. видно хорошо то место, где иголка воткнулась в ткань, и заканчивается один стежок. Это прямо должно быть такое место, где видно, как нитка погрузилась в глубину ткани!

Вот экстремальный пример слишком сильного натяжения. На той стороне, где вы видите практически целиком прямую нить, а от нити на противоположной стороне видите петли – на той натяжение слишком сильное. Т.е. если вы видите такую картину сверху, ослабляйте верхнюю натяжение. Если у вас такая картина снизу – увеличивайте верхнее натяжение.

Но вот мы приблизились к нормальному шву.

Попыталась найти подходящую картинку, но нашла не совсем. Вот, например, шов:

Этот шов ровный, нормальный, не петляет. Можно сказать, что он – ОК. Таким швом можно сшить вещь, она будет держаться, все будет хорошо. Но я бы не стала таким швом делать декоративную строчку на видном месте. Потому что он еще не достаточно “прорисованный”, не достаточно “чеканный”, нету красивого рисунка стежков.Что им не хватает? На верхней картинке все же совсем немного великовато верхнее натяжение, есть прямая линия, нету достаточно красивой глубины стежков (особенно у самого верхнего шва это видно). На второй картинке наоборот – снизу тянет многовато. Шов еще не пострадал так, чтобы им прямо шить было нельзя. Но красота подпорчена. Верхняя нитка слишком погружена в ткань, слишком как-то плоховато прорисована, “тонет”.

Вроде хороший шов, нормальный, ровный, не тянет. Как уже сказано, если шить так, чтобы все швы были на изнанке, можно с таким швом жить долго и счастливо. Но на видном месте я бы таким швом ничего отстрачивать не стала. Хотя все ровно, и ничего в нем не плохо. Но “графика” от него получится не достаточно красивая. Особенно это видно на той части шва, которая ближе к низу. Там шов повернут как бы лицом к нам, видно, что он слишком однородный, как линия. Он не читается как шов. Это – не круто.

Красивый, хороший шов, это – вот:

Нитка погружается в ткань, заходит под ее поверхность, хорошо видно, где кончается один стежок, и начинается другой. Но в самой середине стежка нитка лежит на поверхности ткани, не слишком натянуто. Рисунок ровный, не скачет. И в идеале, если мы перевернем ткань, мы должны увидеть ровно то же самое на другой стороне! Чем одинаковее, тем лучше!

Я тут хочу написать важное:

Настраивать машину так, чтобы ни с одной стороны не было петель, чтобы шов хорошо скреплял слои ткани, и чтобы ничего от шва не собиралось волнами – это само собой разумеется. Без этого вы не сошьете вщь, которой будете довольны. У вас не получится ее никогда хорошо отутюжить, она вечно будет на швах волниться, или шов будет расползаться и слишком сильно виден и.т.д. Это – “программа минимум”.

Но между “швом, который отлично шьет”, и швом, который отлично выглядит” есть вот эта небольшая разница, и ее надо научиться чувствовать. И надо в себе отрастить стремление не останавливаться на “нормальном шве”, а крутить свою машину, пока вы не увидите *красивый* шов. Такой, который действительно украшает вещь, когда он виден снаружи.

И – это очень важно – я уверена, что вот такие по-настоящему красивые швы, это первое, что отличает хорошо сшитую вещь от того, что называют “дурно пахнет хендмейдом”. То, что называют презрительно “самодеятельностью домохозяек” или “Скрипка Самовари”, или “Доморощенное” – это вот когда вешь вроде сшита ровно и хорошо, но все отделано швами, которые “отчетливо пахнут домашней машиной”. На такой шов кто-то посмотрит на улице, и сразу поймет, что это шили дома руками. Потому что промышленные машины так не шьют. Промышленные машины всегда отличаются тем, что натяжение у них настроено идеально. (Оно там автоматически настраивается, и там в любом случае нитки встречаются ТОЧНО на середине между слоями.)

Следующее, чем отличаются промышленно сшитые вещи – это ровные швы, и идеально выдержанное расстояние от края. Но это – отдельная песня. Этому научиться не так трудно, надо просто не спешить, когда делается видимая строчка.

Источник