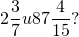как узнать сколько натуральных чисел между числами
Сколько целых чисел между числами
Как найти, сколько целых чисел расположено между данными числами?
Если таких целых чисел немного, их можно перечислить и посчитать.
Например, между числами 26 и 32 находятся целые числа 27; 28; 29; 30; 31. Значит, между 26 и 32 расположено пять целых чисел.
Если же данные числа разделяет большое количество целых чисел, такой способ не подходит. Давайте разберёмся, как решить эту задачу без перечисления.
Следовательно, из 32 надо вычесть 1 целое число (само число 32) и еще 26 (количество целых чисел от 1 до 26 включительно): 32-1-26=5.
Итак, чтобы найти, сколько целых чисел расположено между положительными целыми числами n и m (m>n), надо из большего числа вычесть 1 и ещё меньшее число: k=m-1-n.
Сколько целых чисел расположено между 7 и 329?
А как подсчитать количество целых чисел между числами, которые сами целыми не являются?
Рассмотрим следующий пример. Между числами 26,3 и 32,7 находятся целые числа 27, 28, 29, 30,31, 32. В отличие от предыдущего примера, последнее число, 32, в искомые целые числа входит: k=32-26=6.
Таким образом, чтобы найти количество целых чисел между нецелыми положительными числами n и m (m>n), надо из целой части большего числа вычесть целую часть меньшего числа.
Сколько целых чисел расположено между числами
А как быть, если одно из чисел — отрицательное?
Найдем, например, сколько целых чисел расположено между числами — 4 и 8.
Нуль также является целым числом.
Между нулём и 8 есть 7 целых чисел.
Вывод: количество k целых чисел между отрицательным числом n и положительным m равно k=|n|-1+1+m+1.
То есть, чтобы найти, сколько целых чисел расположено между нецелым отрицательным числом n и нецелым положительным числом m, надо сложить модуль целой части n, 1 и целую часть m.
Сколько целых чисел содержится между числами
6. Сколько чисел в натуральном ряду между числами. 5 класс Математика Никольский С.М.
6.
Сколько чисел в натуральном ряду между числами:
а) 1 и 29; б) 1 и 38; в) 30 и 38; г) 100 и 125?
1, 73, 99, 3049,438108, 999999.
У Алёши 80 марок, у Бори на 20 %
больше, чем у Алёши. У Вовы на 25 %
меньше, чем у Алёши. Сколько марок ( Подробнее. )
Какой угол (в градусах) описывает минутная стрелка за 29 минут?
( Подробнее. )
Кто-нибудь выполнил данное упражнение? Прочитайте стихотворение выразительно, выделяя интонацией повествовательные, вопросительные и ( Подробнее. )
Здравствуйте! На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали ( Подробнее. )
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Как найти количество цифр между двумя заданными?
Не знаю, за что меня заминусовали, вот написал простенькую функцию:
Встроенная функция вычитания подойдет для этого =)
N — первое число
M — второе число
количество цифр между ними равно (M-N-1)
проверка: N = 3, M = 12, тогда M-N-1=12-3-1=8
Если кол-во чисел, то выше сказали уже. Если именно цифр, то что-то подсказывает, что не очень сложно.
Берем кол-во цифр в граничных числах.
И тут у нас 2 варианта по сути:
— Кол-во цифр равно.
— Кол-во цифр не равно, в этом случае здесь обязательно есть крайние поддиапазоны и возможно 1 и более диапазонов между ними. Диапазоны — это набор чисел с одним кол-вом цифр.
1й вариант.
(правое значение — левое значение + 1) * кол-во цифр для диапазона
2й вариант подробнее.
Для крайних диапазонов кол-во цифр будет что-то типа, для левого: (максимальное число с текущим кол-во цифр — левое значение + 1) * кол-во цифр для диапазона, для правого для правого (текущее значение — минимальное число с текущим кол-во цифр + 1) * кол-во цифр для диапазона.
Ну и для средних в цикле (максимальное число с текущим кол-во цифр — минимальное число с текущим кол-во цифр + 1) * кол-во цифр для диапазона).
Кол-во цифр для диапазона — это кол-во цифр для 1го числа из диапазона чисел с одним кол-во цифр.
Если еще надо будет учесть к примеру пробелы, то их можно посчитать как в 1м варианте.
Что-то такое мне подсказывает мой больной мозг не вдаваясь вообще в математическую теорию.
Числа. Натуральные числа.
Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Всякое натуральное число легко записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000. – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Обозначение натуральных чисел: Множество натуральных чисел обозначают символом N.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Сравнение натуральных чисел.
Таблица разрядов и классов чисел.
1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч
1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов
4-й класс миллиарды
1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы.
Основные свойства натуральных чисел.
Действия над натуральными числами.
1. Сложение натуральных чисел результат: сумма натуральных чисел.
Формулы для сложения:
В основном, сложение натуральных чисел выполняется « столбиком ».
2. Вычитание натуральных чисел – операция, обратная сложению: разница натуральных чисел.
Формулы для вычитания:
Вычитание натуральных чисел удобно производить « столбиком ».
3. Умножение натуральных чисел : произведение натуральных чисел.
Формулы для умножения:
(а + b) ∙ с= а ∙ с + b ∙ с
(а – b) ∙ с = а ∙ с – b ∙ с
4. Деление натуральных чисел – операция, обратная операции умножения.
Формулы для деления:
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо.
Когда в выражении есть скобки – сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.