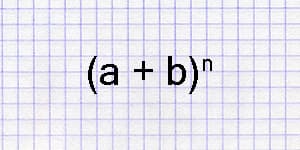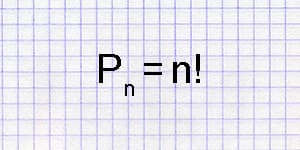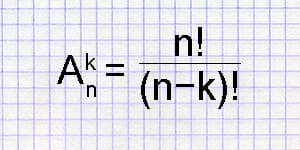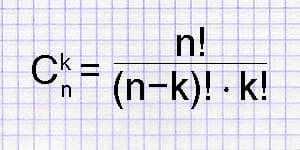как узнать сколько вариантов комбинаций
Комбинаторика
Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.
Правила в комбинаторике
Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.
Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n1 способом, второе n2 и далее до nk, то все действия этой последовательности можно выполнить n1 · n2 · nk способами.
Элементы комбинаторики
Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: Pn = n!
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Элементы комбинаторики. Перестановки, размещения, сочетания
Подсчет числа перестановок, размещений и сочетаний.
Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.
Элементы комбинаторики. Перестановки, размещения, сочетания
Итак, есть множество из n элементов.
Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА
Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m
Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ
Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:
Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC
Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m
Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ
Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:
Как посчитать количество возможных вариантов
Определение числа сочетаний
На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета).
Найти сочетания из n по k
Видеоролик о сочетаниях
Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Полезные ссылки
Решебник по ТВ
Решебник с задачами по комбинаторике и теории вероятностей:
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*. *nk.
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая – из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2.
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n1*n2*n3=6*7*4=168.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается An m и вычисляется по формуле:
Замечание: n!=1*2*3*. *n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Число сочетаний из n элементов по m
Число сочетаний обозначается Cn m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
Подсчет числа перестановок, размещений и сочетаний.
Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.
Элементы комбинаторики. Перестановки, размещения, сочетания
Итак, есть множество из n элементов.
Вариант упорядочивания данного множества называется перестановкой (permutation).
Например, есть множество, состоящее из 3 элементов – А, В, и С. Пример перестановки — СВА. Число всех перестановок из n элементов:
Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА
Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m
Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ
Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:
Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC
Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m
Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ
Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:
Как узнать сколько вариантов комбинаций
Обнаружен блокировщик рекламы
Ой! Похоже, вы используете Adblocker!
Поскольку мы изо всех сил пытались сделать для вас онлайн-расчеты, мы обращаемся к вам с просьбой предоставить нам разрешение, отключив Adblocker для этого домена.
ДОБАВИТЬ ЭТОТ КАЛЬКУЛЯТОР НА ВАШ ВЕБ-САЙТ:
Добавьте калькулятор комбинаций на свой сайт, чтобы упростить использование этого калькулятора напрямую. Создайте учетную запись для этого виджета без проблем, поскольку он на 100% бесплатный, простой в использовании и вы можете добавить его на несколько онлайн-платформ.
Загрузите приложение «Калькулятор комбинаций» для мобильного телефона, чтобы вы могли рассчитать свои значения в своей руке.
Онлайн-калькулятор сочетаний позволяет вам найти количество возможных комбинаций, которые могут быть получены из элементов выборки из большого набора данных. Кроме того, этот комбинаторика калькулятор показывает каждую комбинацию набора данных. По сути, комбинация – это количество способов получить r элементов из n объектов набора данных, где замены не разрешены. Прочтите статью полностью, чтобы точно узнать о ее формуле, ручном расчете, о том, как найти комбинацию с помощью этого калькулятора комбинаций и многом другом.
Кроме того, вы можете попробовать наш онлайн-калькулятор перестановок, который поможет вам найти количество возможных подмножеств, включая подмножество одного и того же элемента в разном порядке.
Что такое формула комбинирования?
Формула для определения количества возможных комбинаций выглядит следующим образом:
n – общее количество в наборе данных
r – это номер, который вы выбираете из этого набора данных & nCr – количество комбинаций
Наш калькулятор NCR использует эту формулу для точных и быстрых вычислений всех элементов набора данных.
Формула сочетания с повторением:
Если нас не волнует повторение, то формула NCR выглядит так:
Здесь на рисунке показаны четыре типа выбора:
Восклицательный знак (!) Используется для факториала числа. Чтобы найти факториал числа, вы также можете попробовать наш онлайн-калькулятор факториала, который поможет вам вычислить факториал для заданных n чисел.
Как рассчитать комбинации (шаг за шагом):
Расчет комбинаций становится очень простым с этим комбинаторным калькулятором и пониманием следующего ручного примера:
Пример:
Директор выбирает 4 учеников из класса, всего 30 учеников, для соревнований по легкой атлетике. Он хочет определить, сколько комбинаций из 4 учеников можно создать из 30 учеников?
Решение:
Общее количество студентов (n) = 30
Выбранные ученики (r) = 4
30C4 = 30 * 29 * 28 * 27 * 26! / 4! (26)!
30C4 = 30 * 29 * 28 * 27/4!
30C4 = 30 * 29 * 28 * 27/4 * 3 * 2 * 1
30C4 = 27405 Возможные команды
Вы можете попробовать этот онлайн-калькулятор сочетаний, чтобы проверить все примеры комбинаций для пояснения.
Комбинации и перестановки:
В английском языке мы используем словосочетание, не задумываясь о важности порядка слов или нет. Просто мой обед состоит из бургера, сэндвича с Рубеном и яблочного пирога. Нас не волнует их порядок, они также могут быть в «сэндвиче с Рубеном, яблочном пироге и бургере», но это та же еда. Также,
Замок сейфа – 584. Теперь, если нас не заботит порядок, то он не работает. Например, 845 не подойдет, а 458 не подойдет. Надо точно ввести 5-8-4. Итак, мы пришли к выводу, что:
Когда порядок не имеет значения, это комбинация, а когда порядок имеет значение, это перестановка. Проще говоря, перестановка – это упорядоченная комбинация.
Как использовать онлайн-калькулятор сочетаний:
Онлайн-калькулятор комбинаций чисел требует различных значений для точного расчета, это шаги, которые вы должны выполнить, чтобы получить мгновенные результаты.
Входы:
Выходы:
Как только вы закончите, калькулятор формулы комбинации покажет:
Заметка:
Не беспокойтесь, хотите ли вы получить расчет с комбинацией или повторением, все, что вам нужно, чтобы выбрать соответствующую опцию, калькулятор комбинации покажет вам результат в соответствии с заданными значениями.
Часто задаваемые вопросы (FAQ):
Что означает 10 выбирают 3?
Это означает выбор 3 элементов из 10 общих элементов без как посчитать количество комбинаций. Он генератор комбинаций 120 возможных комбинаций.
Для чего используется комбинация?
Он определяет возможные расположения в коллекции из n элементов. Помогает выбирать предметы в любом порядке. Это условие непонятно при перестановке числа.
Конечное примечание:
К счастью, вы узнали, что комбинации используются для определения возможных расположений в коллекции n элементов. Когда дело доходит до вычисления большого числа, воспользуйтесь бесплатным онлайн-калькулятор сочетаний, который поможет вам найти комбинацию данных элементов.
Комбинаторика
Комбинаторика онлайн калькуляторы
| Элементы комбинаторики перестановки, размещения, сочетания | Число перестановок находит все варианты перестановки |
| Обратная перестановка онлайн калькулятор | Количество инверсий в перестановке это количество пар элементов |
| Циклическая перестановка перевод цикла в стандарт | Число сочетаний вычисление числа сочетаний из n по k элементов |
| Порядок перестановки стандартной и циклической | Число сочетаний с повторениями онлайн калькулятор для нахождения сочетаний |
| Число размещений нахождение количества размещений | Разложение Бинома Ньютона калькулятор разложения степени |
| Комбинаторные уравнения решение комбинаторных уравнений |
Смотрите также
Сколько существует трёхзначных чисел, которые делятся на 5?
Подскажите что использовать, перестановки с повторениями? Есть восемь элементов у каждого элемента может быть два состояния. Сколько может быть комбинаций?
составьте всевозможные перестановки из элементов множества А, если а=
У Васи есть кубики трех цветов. Он строит из них башню, ставя каждый следующий кубик на предыдущий. Запрещено использовать более 7 кубиков каждого из цветов. Вася заканчивает строить башню, как только в ней окажется по 7 кубиков каких-то двух цветов. Сколько различных башен может построить Вася?
Сколько существует четырехзначных чисел, в запись которых входит ровно одна цифра 3?
Рассмотрим четыре случая:
1) Когда число начинается на 3.
Каждый разряд (сотен, десятков и единиц) можно выбрать девятью способами.
9 × 9 × 9 = 729 чисел.
2) Когда цифра 3 в разряде сотен.
Первую цифру можем выбрать восемью способами, а третью и четвертую – девятью способами, получаем.
8 × 9 × 9 = 648 чисел.
3) Когда цифра 3 в разряде десяток.
8 × 9 × 9 = 648 чисел.
4) Когда цифра 3 в разряде единиц.
8 × 9 × 9 = 648 чисел.
Общее количество: 729 + 648 + 648 + 648 = 2673 чисел.