как узнать скорость волны
Как узнать скорость волны
108 дн. с момента
до конца учебного года
Длина волны. Скорость распространения волны.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [ λ ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц
Свойства волн: длина, частота и скорость
Физика > Длина волны, частота в соотношении со скоростью
Характеристика волны – длина, скорость и частота. Узнайте, что такое частота на графике волны, фазовая и групповая скорость, распространение волны и амплитуда.
Волны характеризуются по частоте, длине и амплитуде. Есть также два типа скорости: фазовая и групповая.
Задача обучения
Основные пункты
Термины
Пример
Если мы рассмотрим видимый свет, то можем отобразить его как электромагнитную волну. Она будет представлена электрическими и магнитными полями, смещающимися в среде. Частоту определяют как цвет: 4 × 10 14 Гц (красный), 8 × 10 14 Гц (фиолетовый), а между ними – все остальные. Длина волны существует в обратной пропорциональности частоте: чем больше частота, тем короче длина.
Свойства волн
Волны характеризуются по их свойствам. Амплитуда представляет половину дистанции от гребня к впадине. Также можно заметить длину волны – пространственный период (от гребня к гребню), обозначающийся буквой λ.
Частота – количество пройденных циклов за определенный временной промежуток. В виде формулы:
Красная волна наделена низкочастотным синусом, поэтому наблюдается мало повторений циклов. А вот у фиолетовой высокая частота. Заметьте, что время растет по горизонтали
f = 1/T (T – период колебаний).
Частота и длина волны также могут быть связаны друг с другом по отношению к «скорости» волны. Получаем:
v = fλ (v – скорость волны или фазовая скорость, с которой фаза волны распространяется в пространстве).
Есть также групповая скорость волны – показатель, с которым общая форма волновых амплитуд (модуляция или огибающая волны) распространяется в пространстве.
Перед вами волна с групповой (положительная) и фазовой (отрицательная) скоростями, движущихся в разных направлениях
Длина и скорость волны.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.
Формула 

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Формула скорости волны
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
\[Ф_s=\omega t-kx+\varphi \ \left(1\right),\]
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
Для нахождения скорости распространения продольных волн в газе применяют выражение:
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
Примеры задач с решением
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
Найдем период колебаний как время одного полного колебания:
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
Вычислим искомую скорость:
Решение. Фазовую скорость движения волны найдем как:
Вычислим фазовую скорость:
\[v=450\cdot 0,8=360\ \left(\frac<м><с>\right).\]
Скорость колебания частиц равна:
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
Циклическую частоту найдем как:
Вычислим максимальную скорость колебаний частиц:
Скорость волн. Характеристики волны
Звуковая волна — это механическая продольная волна определенной частоты. В статье мы разберемся, что такое продольные и поперечные волны, почему не каждая механическая волна является звуковой. Узнаем скорость волны и то, на каких частотах возникает звук. Выясним, одинаков ли звук в разных средах и научимся находить его скорость по формуле.
Появление волны
Представим водную гладь, например пруд в тихую погоду. Если бросить камень, то на поверхности воды мы увидим расходящиеся от центра круги. А что будет, если мы возьмем не камень, а мяч и будем приводить его в колебательное движение? Круги будут постоянно порождаться колебаниями мяча. Мы увидим примерно то же, что изображено на компьютерной анимации.

Если на некотором расстоянии от мяча мы опустим поплавок, то он тоже будет колебаться. Когда колебания с течением времени расходятся по пространству, этот процесс называется волной.
Для изучения свойств звука (длины волны, скорости волны и др.) подходит известная игрушка «Радуга», или Happy Rainbow.
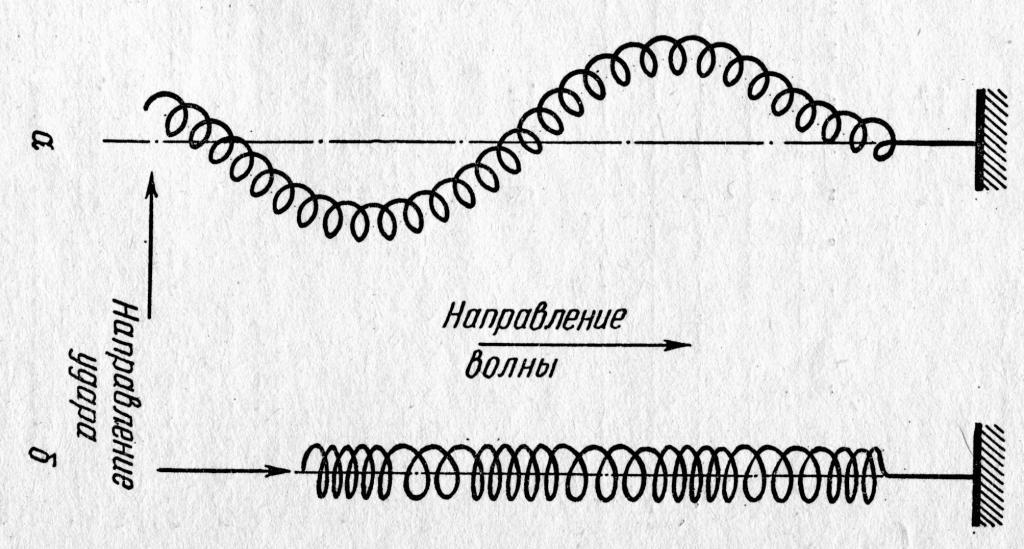
Растянем пружинку, дадим ей успокоиться и резко встряхнем движением вверх-вниз. Мы увидим, что появилась волна, которая побежала по пружинке, а затем вернулась обратно. Это значит, что она отразилась от препятствия. Мы наблюдали, как волна распространялась по пружинке с течением времени. Частицы пружинки двигались вверх-вниз по отношению к своему равновесию, а волна бежала влево-вправо. Такая волна называется поперечной. В ней направление ее распространения перпендикулярно направлению колебания частиц. В нашем случае средой распространения волны была пружинка.

Теперь растянем пружинку, дадим ей успокоиться и дернем вперед-назад. Мы увидим, что витки пружинки сжимаются вдоль нее. Волна бежит в этом же направлении. В одном месте пружинка более сжата, в другом более растянута. Такая волна называется продольной. Направление колебания ее частиц совпадает с направлением распространения.
Представим плотную среду, например, твердое тело. Если мы будем деформировать его сдвигом, возникнет волна. Она появится, благодаря действующим только в твердых телах силам упругости. Эти силы играют роль возвращающих и порождают упругую волну.
Многие думают, что жидкости несжимаемы, однако это не так. Если надавить на поршень шприца с водой, она немного сожмется. В газах тоже возможна деформация сжатия-растяжения. При нажатии на поршень пустого шприца воздух сжимается.
Скорость и длина волны
Вернемся к анимации, которую мы рассматривали в начале статьи. Выберем произвольную точку на одном из расходящихся от условного мяча кругов и проследим за ней. Точка удаляется от центра. Скорость, с которой она перемещается, — это скорость движения гребня волны. Можем сделать вывод: одна из характеристик волны — это скорость волны.
Почему не всякая механическая волна является звуковой
Возьмем алюминиевую линейку.
Она упругая, поэтому подойдет для опыта. Положим линейку на край стола и прижмем рукой так, чтобы она сильно выступала. Надавим на ее край и резко отпустим — свободная часть начнет вибрировать, но звука при этом не будет. Если выдвинуть линейку только чуть-чуть, то колебания короткого края создадут звук.
Что показывает этот опыт? Он демонстрирует, что звук возникает только тогда, когда тело движется достаточно быстро, когда скорость волны в среде высока. Введем еще одну характеристику волны — частоту. Эта величина показывает, сколько колебаний в секунду совершает тело. Когда мы создаем в воздухе волну, то звук возникает при определенных условиях — при достаточно большой частоте.
Важно понимать, что звук — это не волна, хотя он и имеет отношение к механическим волнам. Звук — это ощущение, которое возникает при попадании в ухо звуковых (акустических) волн.
Вернемся к линейке. Когда выдвинута большая часть, то линейка колеблется и не издает звук. Создается ли при этом волна? Конечно, но это механическая волна, а не звуковая. Теперь можно дать определение звуковой волне. Это механическая продольная волна, частота которой находится в диапазоне от 20 Гц до 20 тыс. Гц. Если частота меньше 20 Гц или больше 20 КГц, то мы ее не услышим, хотя колебания и возникнут.
Источник звука
Источником акустических волн может быть любое колеблющееся тело, для этого только нужна упругая среда, например, воздух. Вибрировать может не только твердое тело, но и жидкость, и газ. Воздух как смесь нескольких газов может быть не только средой распространения — он сам способен порождать акустическую волну. Именно его колебания лежат в основе звучания духовых инструментов. Флейта или труба не колеблются. Это воздух разреживается и сжимается, придает определенную скорость волне, в результате чего мы слышим звук.
Распространение звука в разных средах
Мы выяснили, что звучат разные вещества: жидкие, твердые, газообразные. То же самое касается способности проводить акустическую волну. Звук распространяется в любой упругой среде (жидкой, твердой, газообразной), кроме вакуума. В безвоздушном пространстве, допустим на Луне, мы не услышим звука вибрирующего тела.
Большая часть звуков, воспринимаемых человеком, распространяется в воздухе. Рыбы, медузы слышат акустическую волну, расходящуюся по воде. Мы, если нырнем под воду, тоже услышим шум проплывающей рядом моторной лодки. Причем длина волны и скорость волны будут выше, чем в воздухе. Это значит, что звук мотора первым услышит человек, плавающий с аквалангом под водой. Рыбак, который в этом же месте сидит в своей лодке, услышит шум позже.
Скорость звука
Скорость звуковой волны, если рассматривать один и тот же звук, будет неодинаковой в разных средах. Чем плотнее среда, тем быстрее звук достигает нашего уха. Поезд может ехать так далеко от нас, что стук колес будет еще не слышен. Однако если приложить ухо к рельсам, мы отчетливо услышим гул.
Это говорит о том, что в твердых телах звуковая волна бежит быстрее, чем в воздухе. На рисунке представлены значения скорости звука в разных средах.
Уравнение волны
Скорость, частота и длина волны взаимосвязаны. У тел, которые вибрируют с высокой частотой, волна короче. Низкочастотные звуки слышны на большем расстоянии, потому что у них длиннее волна. Существует два уравнения волны. Они иллюстрируют взаимозависимость характеристик волны друг от друга. Зная любые две величины из уравнений, можно вычислить третью:
где с — скорость, ν — частота, λ — длина волны.
Второе уравнение акустической волны:
где Т — это период, т. е. время, за которое тело совершает одно колебание.