как узнать сложность алгоритма
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
13–15 сентября, Онлайн, Беcплатно
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
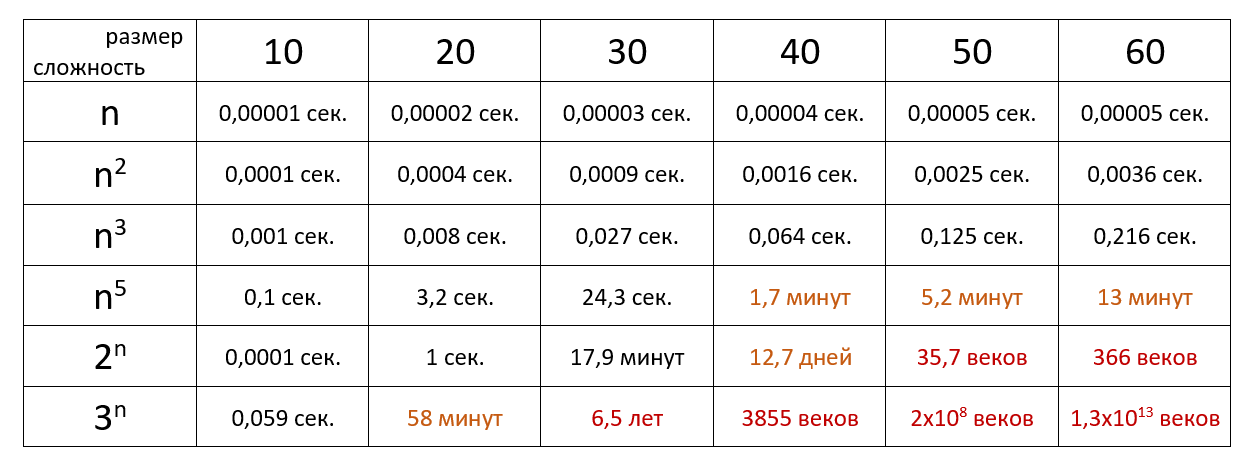
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
Оценка сложности алгоритмов
Введение
Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.
Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.
Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.
Определения
Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.
Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.
Порядок роста сложности алгоритмов
Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.
Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.
Виды асимптотических оценок
O – оценка для худшего случая
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 n0.
Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).
Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.
Примеры асимптотических функций
| f(n) | g(n) |
|---|---|
| 2n 2 + 7n — 3 | n 2 |
| 98n*ln(n) | n*ln(n) |
| 5n + 2 | n |
| 8 | 1 |
Ω – оценка для лучшего случая
Критерии оценки сложности алгоритмов
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.
Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.
Пример оценки сложности при вычислении факториала
Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:
Временная сложность при равномерном весовом критерии
Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).
Таким образом, временная сложность при РВК равна O(n).
Временная сложность при логарифмическом весовом критерии
В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.
Итак, в данной задаче выделяется три операции:
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Введение в анализ сложности алгоритмов (часть 1)
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы покажутся чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он будет полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.
Введение
Многие современные программисты, пишущие классные и широко распространённые программы, имеют крайне смутное представление о теоретической информатике. Это не мешает им оставаться прекрасными творческими специалистами, и мы благодарны за то, что они создают.
Тем не менее, знание теории тоже имеет свои преимущества и может оказаться весьма полезным. В этой статье, предназначенной для программистов, которые являются хорошими практиками, но имеют слабое представление о теории, я представлю один из наиболее прагматичных программистских инструментов: нотацию «большое О» и анализ сложности алгоритмов. Как человек, который работал как в области академической науки, так и над созданием коммерческого ПО, я считаю эти инструменты по-настоящему полезными на практике. Надеюсь, что после прочтения этой статьи вы сможете применить их к собственному коду, чтобы сделать его ещё лучше. Также этот пост принесёт с собой понимание таких общих терминов, используемых теоретиками информатики, как «большое О», «асимптотическое поведение», «анализ наиболее неблагоприятного случая» и т.п.
Этот текст также ориентирован на учеников средней школы из Греции или любой другой страны, участвующих в Международной олимпиаде по информатике, соревнованиях по алгоритмам для учащихся и тому подобном. Как таковой, он не требует предварительного знания каких-либо сложных математических моментов и просто даст вам основу для дальнейшего исследования алгоритмов с твёрдым пониманием стоящей за ними теории. Как тот, кто в своё время много участвовал в различных состязаниях, я настоятельно рекомендую вам прочитать и понять весь вводный материал. Эти знания будут просто необходимы, когда вы продолжите изучать алгоритмы и различные передовые технологии.
Я надеюсь, что это текст будет полезен для тех программистов-практиков, у которых нет большого опыта в теоретической информатике (то, что самые вдохновлённые инженеры-программисты никогда не ходили в колледж, уже давно свершившийся факт). Но поскольку статья предназначена и для студентов тоже, то временами она будет звучать, как учебник. Более того, некоторые темы могут показаться вам чересчур простыми (например, вы могли сталкиваться с ними во время своего обучения). Так что, если вы чувствуете, что понимаете их — просто пропускайте эти моменты. Другие секции идут несколько глубже и являются более теоретическими, потому что студенты, участвующие в соревнованиях, должны разбираться в теории алгоритмов лучше, чем средний практик. Но знать эти вещи не менее полезно, а следить за ходом повествования не так уж сложно, так что они, скорее всего, заслуживают вашего внимания. Оригинальный текст был направлен учащимся старшей школы, никаких особых математических знаний он не требует, поэтому каждый, имеющий опыт программирования (например, знающий, что такое рекурсия) способен понять его без особых проблем.
В этой статье вы найдёте много интересных ссылок на материалы, выходящие за рамки нашего обсуждения. Если вы — работающий программист, то вполне возможно, что знакомы с большинством из этих концепций. Если же вы просто студент-новичок, участвующий в соревнованиях, переход по этим ссылкам даст вам информацию о других областях информатики и разработки программного обеспечения, которые вы ещё не успели изучить. Просмотрите их ради увеличения собственного багажа знаний.
Нотация «большого О» и анализ сложности алгоритмов — это те вещи, которые и программисты-практики, и студенты-новички часто считают трудными для понимания, боятся или вообще избегают, как бесполезные. Но они не так уж сложны и заумны, как может показаться на первый взгляд. Сложность алгоритма — это всего лишь способ формально измерить, насколько быстро программа или алгоритм работают, что является весьма прагматичной целью. Давайте начнём с небольшой мотивации по этой теме.
Мотивация
Мы уже знаем, что существуют инструменты, измеряющие, насколько быстро работает код. Это программы, называемые профайлерами (profilers), которые определяют время выполнения в миллисекундах, помогая нам выявлять узкие места и оптимизировать их. Но, хотя это и полезный инструмент, он не имеет отношения к сложности алгоритмов. Сложность алгоритма — это то, что основывается на сравнении двух алгоритмов на идеальном уровне, игнорируя низкоуровневые детали вроде реализации языка программирования, «железа», на котором запущена программа, или набора команд в данном CPU. Мы хотим сравнивать алгоритмы с точки зрения того, чем они, собственно, являются: идеи, как происходит вычисление. Подсчёт миллисекунд тут мало поможет. Вполне может оказаться, что плохой алгоритм, написанный на низкоуровневом языке (например, ассемблере) будет намного быстрее, чем хороший алгоритм, написанный языке программирования высокого уровня (например, Python или Ruby). Так что пришло время определиться, что же такое «лучший алгоритм» на самом деле.
Алгоритм — это программа, которая представляет из себя исключительно вычисление, без других часто выполняемых компьютером вещей — сетевых задач или пользовательского ввода-вывода. Анализ сложности позволяет нам узнать, насколько быстра эта программа, когда она совершает вычисления. Примерами чисто вычислительных операций могут послужить операции над числами с плавающей запятой (сложение и умножение), поиск заданного значения из находящейся в ОЗУ базы данных, определение игровым искусственным интеллектом (ИИ) движения своего персонажа таким образом, чтобы он передвигался только на короткое расстояние внутри игрового мира, или запуск шаблона регулярного выражения на соответствие строке. Очевидно, что вычисления встречаются в компьютерных программах повсеместно.
Анализ сложности также позволяет нам объяснить, как будет вести себя алгоритм при возрастании входного потока данных. Если наш алгоритм выполняется одну секунду при 1000 элементах на входе, то как он себя поведёт, если мы удвоим это значение? Будет работать также быстро, в полтора раза быстрее или в четыре раза медленнее? В практике программирования такие предсказания крайне важны. Например, если мы создали алгоритм для web-приложения, работающего с тысячей пользователей, и измерили его время выполнения, то используя анализ сложности, мы получим весьма неплохое представление о том, что случится, когда число пользователей возрастёт до двух тысяч. Для соревнований по построению алгоритмов анализ сложности также даст нам понимание того, как долго будет выполняться наш код на наибольшем из тестов для проверки его правильности. Так что, если мы определим общее поведение нашей программы на небольшом объёме входных данных, то сможем получить хорошее представление и о том, что будет с ней при больших потоках данных. Давайте начнём с простого примера: поиска максимального элемента в массиве.
Подсчёт инструкций
В этой статье для реализации примеров я буду использовать различные языки программирования. Не переживайте, если вы не знакомы с каким-то из них — любой, кто умеет программировать, способен прочитать этот код без особых проблем, поскольку он прост, и я не собираюсь использовать какие-либо экзотические фенечки языка реализации. Если вы — студент-олимпиадник, то, скорее всего, пишите на С++, поэтому у вас тоже не должно возникать проблем. В этом случае я также рекомендую прорабатывать упражнения, используя С++ для большей практики.
Максимальный элемент массива можно найти с помощью простейшего отрывка кода. Например, такого, написанного на Javascript. Дан входной массив А размера n :
Анализ наиболее неблагоприятного случая
В теле цикла мы имеем операции поиска в массиве и сравнения, которые происходят всегда:
Асимптотическое поведение
С полученной выше функцией мы имеем весьма хорошее представление о том, насколько быстр наш алгоритм. Однако, как я и обещал, нам нет нужды постоянно заниматься таким утомительным занятием, как подсчёт команд в программе. Более того, количество инструкций у конкретного процессора, необходимое для реализации каждого положения из используемого языка программирования, зависит от компилятора этого языка и доступного процессору (AMD или Intel Pentium на персональном компьютере, MIPS на Playstation 2 и т.п. ) набора команд. Ранее же мы говорили, что собираемся игнорировать условия такого рода. Поэтому сейчас мы пропустим нашу функцию f через «фильтр» для очищения её от незначительных деталей, на которые теоретики предпочитают не обращать внимания.
Имеет смысл думать о 4 просто как о «константе инициализации». Разным языкам программирования для настройки может потребоваться разное время. Например, Java сначала необходимо инициализировать свою виртуальную машину. А поскольку мы договорились игнорировать различия языков программирования, то попросту отбросим это значение.
эквивалентен следующему на Си:
Так что имеет смысл ожидать, что различные языки программирования будут подвержены влиянию различных факторов, которые отразятся на подсчёте инструкций. В нашем примере, где мы используем «немой» паскалевский компилятор, игнорирующий возможности оптимизации, требуется по три инструкции на Паскале для каждого доступа к элементу массива вместо одной на Си. Пренебрежение этим фактором идёт в русле игнорирования различий между конкретными языками программирования с сосредоточением на анализе самой идеи алгоритма как таковой.
Введение в анализ сложности алгоритмов (часть 4)
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.
Оптимальная сортировка
Этот финальный раздел — опциональный. Он несколько сложнее, так что можете не стесняясь пропустить его, если хотите.От вас потребуется сфокусироваться и потратить некоторое время на решение упражнений. Однако, так же здесь будет продемонстрирован очень полезный и мощный способ анализа сложности алгоритмов, что, безусловно, стоит внимания.
Мы рассматривали реализацию сортировки, называемую сортировкой выбором, и упоминали, что она не является оптимальной. Оптимальный алгоритм — это тот, который решает задачу наилучшим образом, подразумевая, что не существует алгоритма, делающего это лучше. Т.е. все прочие алгоритмы для решения данной проблемы имеют такую же или большую сложность. Может существовать масса оптимальных алгоритмов, имеющих одинаковую сложность. Та же проблема сортировки может быть решена оптимально многими способами. Например, мы можем использовать для быстрой сортировки ту же идею, что и при бинарном поиске. Такой способ называется сортировкой слиянием.
Используя эту функцию, мы можем построить лучший алгоритм сортировки. Идея следующая: мы разбиваем массив на две части, рекурсивно сортируем каждую из них и объединяем два отсортированных массива в один. Псевдокод:
Эта функция сложнее предыдущих для понимания, поэтому выполнение следующего упражнения может потребовать у вас больше времени.
Как вы видели в последнем примере, анализ сложности позволяет нам сравнивать алгоритмы, чтобы понять, который из них лучше. Исходя из этих соображений, теперь мы можем быть уверены, что для массивов больших размеров сортировка слиянием намного опередит сортировку выбором. Такое заключение было бы проблематично сделать, если бы мы не имели теоретического базиса анализа разработанных нами алгоритмов. Несомненно, алгоритмы сортировки с временем выполнения Θ( n * log( n ) ) широко используются на практике. Например, ядро Linux использует алгоритм, называемый «сортировкой кучей», который имеет такое же время выполнения, как и сортировка слиянием. Заметим, что мы не будем доказывать оптимальность данных алгоритмов сортировки. Это потребовало бы гораздо более громоздких математических аргументов, но будьте уверены: с точки зрения сложности нельзя найти вариант лучше.
После изучения данной статьи, приобретённая вами интуиция относительно анализа сложности алгоритмов должна будет помогать вам создавать быстрые программы и сосредотачивать усилия по оптимизации на тех вещах, которые действительно имеют большое влияние на скорость выполнения. Всё вместе позволит вам работать более продуктивно. К тому же математический язык и нотации (например, «большое О»), рассмотренные в данной статье, будут вам полезны при общении с другими разработчиками программного обеспечения, когда речь зайдёт о времени выполнения алгоритмов, и, надеюсь, вы сможете применить на практике приобретённые знания.
Вместо заключения
Статья публикуется под Creative Commons 3.0 Attribution. Это означает, что вы можете копировать её, публиковать на своих веб-сайтах, вносить в текст изменения и вообще делать с ней всё, что заблагорассудится. Только не забывайте упоминать при этом моё имя. Единственное но: если вы основываете свою работу на данном тексте, то я настоятельно призываю вас публиковать её под Creative Commons, чтобы облегчить совместную работу и распространение информации.
Спасибо за то, что дочитали до конца!