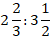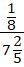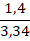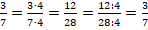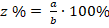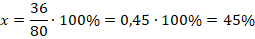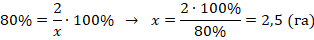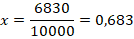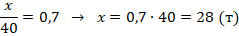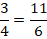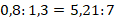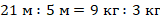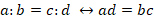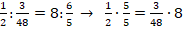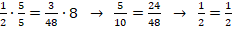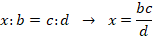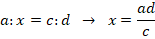как узнать соотношение одного числа к другому

Процент одного числа от другого

Как посчитать сколько процентов составляет одно числа от другого? Задачка решается при помощи бесплатного онлайн калькулятора, который использует для вычисления формулу: Первое число / Второе число * 100%.

Сохранить ссылку

Отправить коллегам

Часто встречаются задачи, в которых требуется определить процентное соотношение одного числа от другого.

Например, маркетолог может готовить отчет для руководства компании, где требуется рассчитать чему равна доля рекламных переходов от общего количества посетителей сайта за последний календарный месяц.

Давайте разберемся: За апрель сайт посетило 53983 уникальных пользователя. По данным аналитических систем из рекламных каналов мы получили 8930 визитов.

Вопрос: Как найти процент рекламных переходов от общего числа уникальных визитов?

Инструкция

Рассчитать эту задачу можно по формуле: Рекламный трафик / Общий трафик * 100%. Однако, вы можете использовать и бесплатный сервис, который моментально произведет нужные вычисления.

Мгновенно получаем ответ — 16,54 % доля переходов с рекламы от общего объёма посетителей ресурса.

Обратная связь

Надеюсь, что инструмент оказался полезным. Если вы обнаружили ошибку или знаете как можно улучшить калькулятор, то обязательно пишите на адрес info@konstantinbulgakov.com. Постараюсь рассмотреть предложения.

И не забывайте писать комментарии в специальной форме или поддерживать проект — сохраняйте ссылку, отправляйте линк коллегам, да и просто напишите доброе слово ниже.

Процент одного числа от другого: 1 комментарий

Большое спасибо за удобнейший инструмент! Объективно-самый удобный из множества предложений, с отличным интерфейсом, где нет ничего лишнего.
Удачи и процветании в Вашем деле!

Источник

Как рассчитать отношение одного числа к другому?

Как вычислить отношение двух чисел?

Рекомендуемый клип · 119 сек.

Математика 6 класс.

Отношение двух чисел — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как рассчитать соотношение 1 к 2?

Как вычислить процентное соотношение двух чисел?

Рекомендуемый клип · 55 сек.

Процентное отношение двух чисел — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как решать отношения и пропорции?

Рекомендуемый клип · 118 сек.

ОТНОШЕНИЯ и ПРОПОРЦИИ — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как правильно решать пропорции?

Рекомендуемый клип · 40 сек.

Как решать задачи на пропорции? — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Что такое отношение двух чисел?

Частное двух чисел называют отношением этих чисел.

a — предыдущий член отношения, b — последующий член отношения. a и b должны быть отличны от нуля. Отношение показывает, во сколько раз первое число больше второго либо какую часть первое число составляет от второго.

Что такое масштаб 1 к 2?

Масштабом называют отношение линейных размеров изображения предмета на чертеже к действительным размерам этого предмета. Размеры предмета на чертеже могут быть меньше действительных или больше. Масштаб 2:1 означает, что изображение на чертеже (рисунке) в два раза больше изображаемого объекта.19 янв. 2015 г.

Как понять соотношение 1 к 10?

Как рассчитать процентное соотношение?

Процентное отношение определяет, какой процент от целого составляет данное число. Для нахождения процента нужно разделить одно число на другое и умножить на 100%. Пример: Процентное соотношение числа 25 от 50 будет составлять 50%, так как 25/50×100%=50%.

Как посчитать процент из двух чисел в Excel?

Как посчитать процент от числа в Excel

Как в Excel посчитать процент одного числа от другого?

Рекомендуемый клип · 65 сек.

как считать проценты в Excel — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как отношение перевести в проценты?

Процент записывается с помощью знака «%».

Как рассчитать отношение?

Как составить пропорцию 6 класс?

Рекомендуемый клип · 112 сек.

Математика 6 класс. Пропорции — YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Что такое отношение в пропорции?

Отношение – это частное от деления одного числа на другое. Пропорция – это равенство двух отношений. Средние члены пропорции: 20 и 3 в первой пропорции; b и с – во второй. Основное свойство пропорции: Произведение крайних членов пропорции равно произведению её средних членов.

Источник

Отношение. Процентное отношение двух чисел

Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.

Отношение двух чисел показывает:

Процентное отношение

Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.

Например: вычислить, сколько процентов составляет число 52 от числа 400.

Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).

Примеры.

Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?

1 200 изделий – это план завода, или 100% плана.

1) Сколько изделий изготовил завод сверх плана?

2 300 – 1 200 = 1 100 (изд.)

2) Сколько процентов от плана составят сверхплановые изделия?

1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?

2) На сколько процентов перевыполнен план?

Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?

Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:

Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).

Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?

Приведите отношение дробных чисел к отношению натуральных чисел.

В классе 25 учеников, 40% из них – девочки. Сколько девочек в классе?

В саду растет 5 кустов желтых роз, что составляет 25 % всех посаженных в саду кустов роз. Сколько всего кустов роз высажено в саду?

На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке?

Турист проехал до базы отдыха 80 км, что составляет 40 % всего расстояния. Сколько километров осталось преодолеть туристу до базы?

Сплав содержит 20% железа и 40% меди, остальное – бронза. Определите массу бронзы, если масса сплава составляет 5 кг.

Источник

Нахождение процентного отношения двух чисел

Отношение двух любых чисел x и y – это их частное, то есть дробь вида x/y. Процентным соотношением таких чисел является частное, умноженное на 100.

История понятия

Процент происходит от латинского выражения «pro cento», которое в переводе означает «на сотню». В математике процент — это сотая часть числа. Выражение частей от целого было актуально еще в античные времена, когда люди впервые начали использовать дроби. В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.

Проценты зародились в Древнем Риме, задолго до возникновения арабской системы чисел. Многие бытовые вопросы, как то мера товаров или размер налога, определялись как сотая часть от целого. В России такие вычисления были введены гораздо позже Петром Первым, ведь русская система мер использовала числа, не кратные сотне. Проценты до сих пор активно используются в реальной жизни и занимают важное место во многих сферах деятельности.

Что такое процент

Итак, процент — это одна сотая часть чего либо. Если у нас есть 100 яблок, то 5 фруктов из них — это пять частей от сотни или 5%. Если у нас есть 200 персиков, то 23% от них означает 23 части по 2 фрукта каждая или 46 персиков. Очевидно, что эти показатели можно выразить в виде обыкновенных дробей. В случае с яблоками мы получим дробь 5 / 100 = 5%, а в ситуации с персиками — 46 / 200 = 23%. Используя данное уравнение, мы можем найти процентное соотношение двух чисел. И не только.

Процентное соотношение двух чисел

Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:

где m – размер части, n – размер целого, p – процент.

Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.

Примеры расчета процентов

Допустим, у нас есть 200 кг сахара. Мы хотим узнать:

Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.

Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2%.

Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18% от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.

Процентная разница между числами

Наш калькулятор также позволяет определить процентную разницу между числами. Для вычисления данного параметра используется простая формула:

(a − b) / (0,5 × (a + b)) × 100%.

Если вам для решения практических задач требуется вычислить процентную разницу между двумя значениями, то достаточно выбрать необходимый пункт в меню калькулятора и рассчитать требуемый показатель.

Пример

Допустим, за первый месяц работы вы получили чистую прибыль в размере 500 долларов, а во втором — 650 долларов. Давайте узнаем, на сколько процентов изменился ваш доход за месяц. Для этого выберите в меню программы тип калькулятора «разница в процентах» и введите заданные показатели прибыли. При этом неважно, в какую из ячеек вы вобьете числа, так как разница в любом случае будет одинакова. В результате мы получим ответ — прибыль изменилась на 26%. В нашем случае она увеличилась.

Заключение

Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе.

Источник

Отношение чисел

Отношения чисел: определение, свойства, виды

Определение

Отношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.

Для обозначения отношения чисел используется знак деления «:» либо черта дроби.

Общая форма записи отношения чисел: a : b или, соответственно, . В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: .

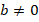
3:2

Здесь 3 и 4 – предыдущие члены отношений, 2 и 9 – последующие.

Свойства отношений

Свойство №1. Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.

Примеры отношений, члены которых являются целыми числами, приведены выше (см. Пример №1).

Пример №2. Отношения, члены которого дробные числа:

Свойство №2. Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел.

Деление членов отношения на одно и то же число называют сокращением отношения.

Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.

Свойство №3. В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»

Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.

Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.

В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта. При этом под абсолютными величинами понимают величины, выраженные в конкретных единицах измерения – кг, км и так далее.

Процентное отношение

Процентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.

Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.

Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.

Пример №6. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?

Обозначим искомую величину через х. Тогда получаем:

Пример №7. Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?

Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:

Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:

Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.

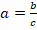
Специальной единицы измерения доля не имеет и измеряется просто в единицах.

Пример №8. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?

Обозначим искомую величину через х. Составим отношение и найдем х:

Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит .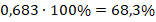

Пример №9. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?

Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:

Пропорция

Пропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как 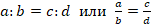, где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.

Пример №9. Примеры конкретных пропорций:

При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.

Основное свойство пропорции: произведение ее крайних членов равно произведению средних. Математически это свойство записывается так:

Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:

Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.

Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.

Математически это выражается так:

То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.

Источник