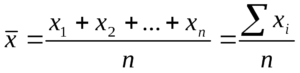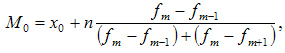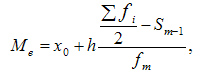как узнать среднее арифметическое чисел
Среднее арифметическое
Предлагаемая здесь программа расчета среднего арифметического умеет не только считать статистические параметры исследуемого множества чисел, но и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.
Среднее арифметическое [1] значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:
Расчет среднего арифметического
Введите исходные данные
Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°
Дисперсия [2] , σ 2
Среднеквадратическое отклонение [3] , σ
Коэффициент вариации [4] , V
Размах вариации [5] , R
Среднее линейное отклонение [6] , δ
Design by Sergey Ov for abc2home.ru
ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:
Сохранить расчет среднего арифметического в истории браузера
Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов
После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего арифметического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.
Страницы по теме «Расчет средних значений»
Свойства среднего арифметического
1. Среднее арифметическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.
2. Кроме того среднее арифметическое подчиняется неравенству о средних для множества положительных вещественных чисел
то есть для любого множества действительных чисел среднее арифметическое никогда не бывает больше среднего квадратического [1] :
Прикладное значение среднего арифметического
Среднее арифметическое значений исследуемых данных находит широкое прикладное применение в метрологии и статистике. При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение будет являться оценкой ошибки измерений, поэтому дисперсия и среднеквадратическое отклонение так же включены в результаты расчетов.
Задания ЕГЭ, на тему «Среднее арифметическое»
Среднее арифметическое 7 натуральных чисел равно 12. К ним добавили восьмое число такое, что среднее арифметическое этих восьми чисел равно 14. Найдите восьмое число.
Согласно оределению среднего арифметического для 7 чисел имеем:
А для 8 чисел получется, что
На доске написано более 40, но менее 50 целых чисел. Среднее арифметическое этих чисел равно −4, среднее арифметическое всех положительных из них равно 5, а среднее арифметическое всех отрицательных из них равно −5.
а). Сколько чисел написано на доске?
б). Каких чисел написано больше: положительных или отрицательных?
в). Какое наибольшее количество положительных чисел может быть среди них?
по определению среднего арифметического сумма множества чисел равна призведению среднего арафметического и их количества и по условию задачи имеем:
(включаем логику [обычную])
а). Очевидно, что левая часть полученного равенства 2.2 делится на 5, поэтому n тоже должно делиться на 5. По условию 40 n n = 45.
Таким образом, написано 45 целых чисел.
б). Подставим в равенство 2.2 полученное для n значение, тогда
в). Для определения наибольшего возможного количества целых положительных чисел удовлетворяющих условиям задачи, возпользуемся выражениями 2.1 и 2.3 с подставленным значением n. С учетом того, что p ≥ 0 получаем:
или подставляя в первое значение m:
Таким образом положительных чисел может быть не более 4.
Ответ: а) 45; б) отрицательных; в) 4.
P.S. На этой странице используется Бета версия программы расчета среднего арифметического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Другие кому-то, возможно, более привычные определения:
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых в этой сумме (Математика, 5 класс).
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых (Алгебра, Макарычев, 7 класс).
2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:
3. Среднеквадратическое отклонение σ вычисляется как корень квадратный от дисперсий и возвращает нас в область сопоставимых со средним арифметическим величин:
4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:
5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:
6. Среднее линейное отклонение определяется как средняя арифметическая величина абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:
Математика
План урока:
Понятие среднего арифметического
К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?
Ответ на вопрос, можно получить двумя способами. Рассмотрим их.
Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.
Разделим конфеты между детьми:
Теперь известно, что каждому ребенку досталось 6 конфет.
Каждой внучке досталось две шоколадки.
Разделим шоколадные яйца:
Выяснили, бабушка привезла по два киндер-сюрприза.
Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:
Получается, бабушка привезла по 10 сладостей.
Запишем решение задачи.
Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.
Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть. Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:
Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:
Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:
Каждой внучке досталось по 10 сладостей.
Запишем решение этой задачи с использованием второго способа.
Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!
Алгоритм нахождения среднего арифметического
Рассмотрим следующую задачу.
Два брата-садовода продавали собранные фрукты. Первый брат продал яблок на 25000 рублей, а второй брат продал груш на сумму 15000 рублей. Все заработанные деньги братья разделили поровну. Сколько денег заработал каждый садовод?
Чтобы ответить на вопрос, необходимо использовать изученное правило.
Чтобы найти среднее арифметическое нескольких чисел, нужно сумму этих чисел разделить на их количество. Для этого:
1. Определяем количество слагаемых;
2. Находим сумму всех слагаемых;
3. Делим полученную сумму на количество слагаемых
В начале давайте определим количество слагаемых. Так как фрукты продавали два садовода, то и делить выручку будем между ними. То есть количество слагаемых в сумме – два.
Теперь можем найти общую сумму, заработанную братьями. Для этого, складываем выручку первого и второго брата:
Всего они заработали 40000 рублей.
Зная, что общая сумма равна 40000 рублей, мы можем найти сумму заработка каждого садовода. Для этого полученную сумму (40000) делим на количество слагаемых (2):
Получается, заработок садовода составил 20000 рублей.
В ходе решения данной задачи мы составили алгоритм нахождения среднего арифметического.
Алгоритм вычисления среднего арифметического:
1. Находим слагаемые и считаем их количество;
2. Суммируем все слагаемые;
3. Полученную сумму делим на количество слагаемых
Держи табличку всегда под рукой, тогда сможешь найти среднее арифметическое любых чисел!
Найди среднее арифметическое чисел 10,20,30,40.
Чтобы выполнить необходимые вычисления, вспоминаем,
Мы уже знаем, что для вычисления заданий, такого вида, существует специальный алгоритм. Используя данный алгоритм,выполним все необходимые действия.
Следуя определенному алгоритму, мы без труда выполнили задание.
Запомни формулу среднего арифметического!
В заключение нашего урока рассмотрим еще одну задачу.
В школе четыре пятых класса 5А,5Б,5В,5Г. 5А – 22 ученика, 5Б –30 учеников, 5В – 28 детей, 5Г – 20. Найдите, сколько детей училось бы в каждом классе, если во всех классах учеников будет поровну.
Исходя из условия, в этой задаче нужно найти среднее количество учеников в одном классе. Чтобы ответить на главный вопрос, необходимо воспользоваться алгоритмом вычисления среднего арифметического.
Значит, если бы во всех пятых классах школы, училось равное количество учеников, в каждом классе было по 25 детей.
Сегодня вы узнали, как найти среднее арифметическое число. Внимательно рассмотрите урок, и запомните основные определения и алгоритмы! Тогда, любая контрольная будет по плечу!
Интересные факты
Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.
Как правильно вычислить среднее значение?
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
Давайте обратимся к классическому примеру со средней зарплатой.
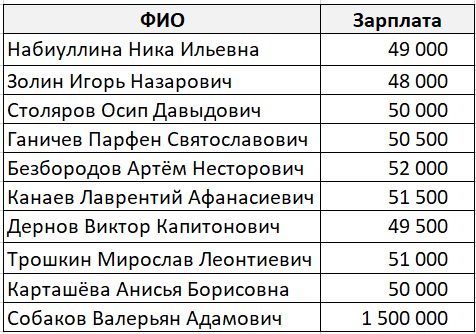
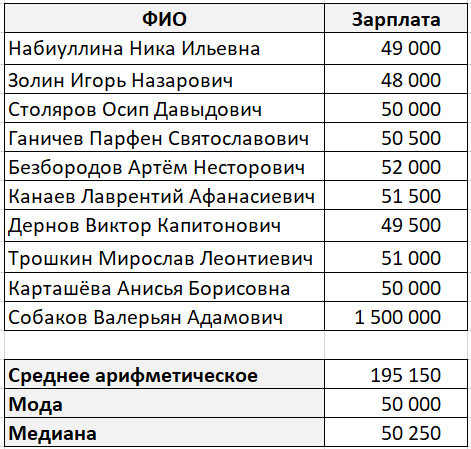
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
И чтобы ее использовать достаточно написать вот такой запрос:
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Вычисляем медиану на SQL
Выглядит все это так:
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
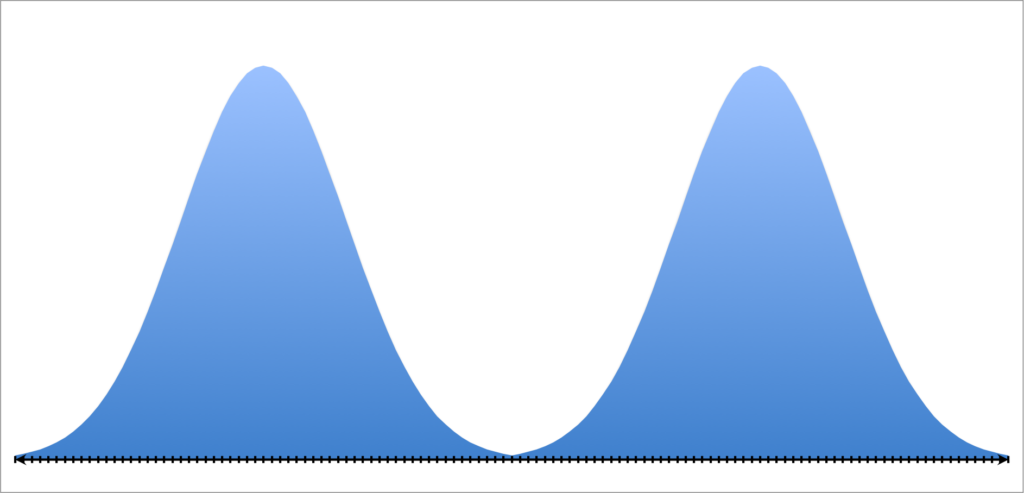
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Как находить и вычислять для двух среднее арифметическое значение
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Подсчёт среднего арифметического пары
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического, можно обратить внимание на то, что у них есть общая закономерность.
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметического.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
(А+В+…+N)/N
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
Видео
Из видео вы узнаете, как находить среднее арифметическое.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.