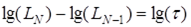как узнать волновое сопротивление антенны
Как узнать волновое сопротивление антенны
Что такое входное сопротивление антенны и что с ним делать?
Все знают, что входное сопротивление (импеданс) антенны редко когда бывает равный волновому сопротивлению фидерной линии. Здесь постараюсь показать, как согласовать нагрузку с фидером эффективными методами. Далее все примеры будут даны для коаксиального кабеля с волновым сопротивлением 50 ом, но принцип расчёта действителен и для других как несимметричных, так и симметричных линий передач.
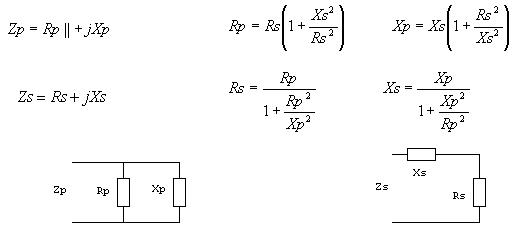
Например, пересчитаем последовательное соединение Zs=40+j30 W в параллельное Zp.
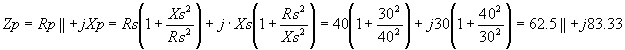
Чаще используют эквивалент последовательного включения, но и эквивалент параллельного включения имеет такое же практическое значение. Zs называется импедансом последовательного включения, R – резистансом, X – реактансом, а Zp импедансом параллельного включения. В параллельном включении часто используется админтанс, но это проводимость, и наглядность при его использовании сильно уменьшается. Обычно термин „импеданс“ указывает, что речь идёт о последовательном соединении эквивалентного активного и реактивного сопротивлений. Однако, пересчёт последовательного соединения сопротивлений в параллельное соединение довольно часто нужен для компенсации реактивной составляющей. Только следует иметь в виду, что при последовательной и параллельной компенсации получаем разные активные составляющие сопротивления. Для пересчёта Zs в Zp и наоборот очень хорошо подходит программа NETCALK. Можно посчитать и здесь.
Rs = Xs = Zp» onclick=»skaiciuok(‘zszp’)»>
Rp = Xp = Zs» onclick=»skaiciuok(‘zpzs’)» />
SWR =
Возникает вопрос, как измерить параметры комплексной нагрузки. К сожалению, простой измеритель КСВ тут мало пригоден. Я для этого пользуюсь векторным анализатором VA1, который на дисплее показывает все нужные цифровые значения.
Компенсация реактивной составляющей
Реактивную составляющую сопротивления (импеданса) полезно компенсировать. Это уменьшает КСВ. Суть компенсации есть выравнивания фаз напряжения и тока. Менять угол фазы между напряжением и током можно подключая реактивный элемент последовательно или параллельно. Чтобы разница в углах фаз стала равна нулю, надо подключить такое реактивное сопротивление, какое присутствует в эквивалентной схеме нагрузки, только с противоположным знаком. Известно, что реактивное сопротивление ёмкости имеет отрицательный знак, индуктивности – положительный. В случае последовательной компенсации дополнительный эквивалентный реактивный элемент с противоположным знаком включается последовательно и получается последовательный контур, а в случае параллельной компенсации – параллельно, получается параллельный контур. В случае последовательного соединения сопротивлений они просто складываются

А в случае параллельного соединения

Как видим, согласовать можно, подключив индуктивность 1,35 m H параллельно нагрузке, а сигнал на нагрузку подавать через конденсатор 68,5pF.
Шлейфы
Шлейфами называются закороченые или открытые отрезки фидера. В идеальном фидере (фидере без потерь) сопротивление таких отрезков есть чисто реактивное, активной части нет. Такими отрезками фидера можно пользоваться при компенсации реактивной составляющей. Это удобно, если применяется параллельное компенсирование. Часто используется отрезки до четверти длины волны. Они могут быть и длиннее, но реальные фидеры имеют потери и, чем длиннее линия, тем больше. Замкнутый шлейф электрической длины до 1/4 l имеет на конце индуктивное реактивное сопротивление, разомкнутый – ёмкостное. Такими отрезками фидера можно имитировать как индуктивность, так и ёмкость. Но надо не забыть, что индуктивность или ёмкость шлейфа зависят от частоты. В приведённом примере мы видим, что надо подключить индуктивность 1,352 m H. С помощью MMANA получаем, что такую индуктивность на 14 MHz имеет закороченный на конце шлейф с кабеля RG58/U длиной 2,62м.
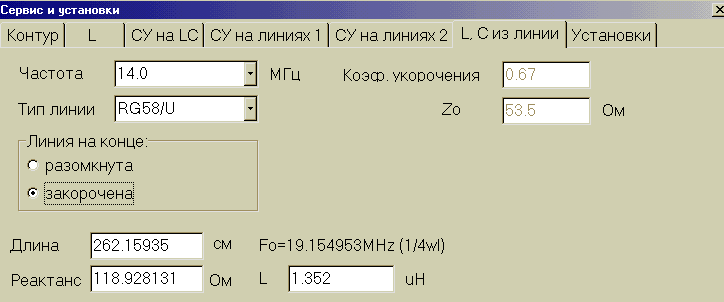
На том же примере попробуем то же согласовать с помощью MMANA другим способом, используя только шлейф.
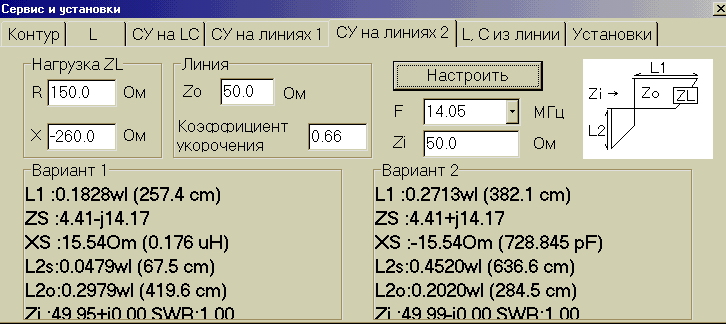
Таким образом, если короткозамкнутый шлейф длиной 67,5см. подключить параллельно фидеру на расстоянии 2,57м. от нагрузки, то так же полностью согласуем фидер с нагрузкой. Или же, можно параллельно подключить разомкнутый шлейф длиной 2,84м. на расстоянии от нагрузки 3,82м. Возможны и другие варианты согласования. Но следует помнить, что потери в низкоомных (коаксиальных) фидерах при больших величинах КСВ значительны, так что желательно выбирать такой способ согласования, при котором получаются самые короткие отрезки фидера с большим КСВ и применять толстые качественные кабеля.
Как видите, практически можно согласовать все и по-разному. Только для этого нужен измерительный прибор, ну, и конечно, компьютер. Комплексное сопротивление антенны не измеришь ни тестером, ни измерителем КСВ. Без этих данных согласование превращается в трудоёмкое занятие и часто приводит к неудовлетворительным результатам. В этой статье я описал несколько методов согласования. Постарался описать суть вопроса как можно проще, но очень просто в таком вопросе не получается.
Эта статья мною написана несколько лет назад на литовском языке и сейчас переведена на русский. В настоящее время имеются другие версии программ APAK-EL и MMANA, примеры же приведены используя старые версии. APAK-EL имеет утилиту, с помощю которой тоже можно рассчитать компенсирующие реактивности. Однако сам принцип согласования от этого не меняется.
Надеюсь, что статья кое-кому будет полезна.
Волновое сопротивление антенн
Приветствую, дорогие друзья. С вами Тимур Гаранин.
В своём видео курсе «Антенны» я уделил особое внимание такой теме как волновое сопротивление и согласование. Тем не менее, я продолжаю получать много вопросов относительно того, как измеряется волновое сопротивление, от чего оно зависит и в принципе, какова его природа.
Начнем с определения. Волновое сопротивление линии — это отношение приложенного к ней напряжения к току, в этой линии.
И сразу покажем, как антенные анализаторы измеряют волновое сопротивление.
Представим что у нас есть полотно антенны из одного тонкого проводника. Подключаем антенный анализатор одним выходом к этому полотну. Второй выход антенного анализатора подключаем к земле, равно как и дальний конец полотна. Внутри антенного анализатора уже встроены вольтметр и амперметр. Что делает антенный анализатор? Он подает на линию единичную ступеньку, то есть просто напряжение определённого уровня. И одновременно с этим измеряет, какой ток потребляет эта линия. И по соотношению напряжения к току определяет волновое сопротивление.
Представим, что к этому же антенному анализатору мы подключаем другое полотно такой же длины, но большей площади поверхности. Антенный анализатор измеряет волновое сопротивление этого полотна, и оно оказывается значительно меньше, чем волновое сопротивление тонкого провода. Почему, от чего зависит волновое сопротивление полотна?
Волновое сопротивление полотна зависит напрямую от его погонных параметров, погонных емкости и индуктивности. Рассчитывается как корень квадратный от отношения погонной индуктивности к погонной емкости. Из чего можно сделать вывод, что чем больше погонная индуктивность и меньше погонная емкость, тем больше это сопротивление.
Хочу обратить особое внимание на то, что волновое сопротивление зависит не просто от емкости и индуктивности антенны, а от погонных емкостей индуктивностей. Мне тут в комментариях кое-кто писал, что чем больше длина антенны, тем больше емкость, а значит меньше волновое сопротивление. Это абсолютно неверно. Волновое сопротивление полотна от длины антенны не зависит вообще.
Представим себе такую ситуацию. У нас есть полотно длиной в метр, и ёмкость этого полотна равна допустим 100 пикофарад. Мы берём и увеличиваем длину этого полотна вдвое, соответственно емкость полотна увеличилась тоже вдвое, и сейчас составляет 200 пикофарад. Но погонная емкость, то есть емкость, деленная на единицу длины, осталась такая же, 100 пикофарад на метр.
То же самое касается и погонной индуктивности.
Погонные параметры по определению от длины не зависят, так как представляют собой параметры, деленные на единицу длины.
Но тогда от чего они зависят?
Допустим у нас есть обыкновенный диполь, выполненный из отрезков относительно тонкого провода. Этот диполь, его отрезки, обладают определёнными погонными емкостью и индуктивностью.
А теперь сравним его с такой антенной как диполь Надененко. Диполь Надененко представляет собой несколько параллельных стержней расположенных по кругу большого радиуса на равном расстоянии друг от друга. Иногда, для еще большего увеличения площади поверхности, диполь Надененко окутывают металлической сеткой.
Я думаю, уже сейчас вам интуитивно понятно, что диполь Надененко будет иметь значительно меньшее волновое сопротивление, чем просто диполь из тонкого провода.
Во-первых, очевидно, что диполь Надененко обладает грандиозно большей площадью поверхности, следовательно имеет очень большую погонную емкость.
Но кроме этого, диполь Надененко имеет еще и меньшую погонную индуктивность. Почему? Каждый из стержней диполя Надененко имеет свою собственную индуктивность. Но так как эти стержни включены параллельно, то и их индуктивности включены параллельно. Как известно, параллельное включение индуктивностей уменьшает общую индуктивность.
Следовательно, диполь Надененко, благодаря своим погонным параметрам, имеет значительно меньшее волновое сопротивление, чем диполь из тонкой проволоки.
Можем сделать вывод, что погонная емкость полотна прямо зависит от площади поверхности полотна на единицу длины. С погонной индуктивностью не всё так очевидно, она зависит от сечения проводника, либо от количества параллельно включенных проводников, и от магнитной проницаемости линии или окружающей среды.
Как измерять погонные параметры антенны при помощи антенного анализатора? Если у нас симметричная антенна, то тут всё просто — один выход антенного анализатора мы включаем к одному вибратору антенны, второй выход — к другому вибратору.
Если же у нас одиночное полотно, то один из выходов анализатора мы должны включить на полотно, а второй — на землю, либо на корпус. Если мы используем корпус, главное требование для него — он должен быть достаточной ёмкости, чтобы принять заряд половины периода колебаний.
Ещё, что очень важно, полотно антенны должно быть отдалено от земли или корпуса на расстояние не менее половины длины волны в пространстве. Почему? Потому что если полотно будет слишком близко к Земле, силовые линии электрического поля полотна будут замыкаться на землю. А мы ведь измеряем не емкость полотна относительно Земли, нас интересует прежде всего емкость полотна относительно себя самого.
Когда речь идёт о диполе, то мы очевидно измеряем емкость одного отрезка диполя относительно другого отрезка диполя. Когда речь идет об единичном полотне, например о полотне антенны бегущей волны, то мы измеряем емкость каждого отрезка этого полотна относительно соседних отрезков этого же полотна. То есть ёмкость полотна относительно себя самого.
Силовые линии электрического поля, начинающиеся на максимумах потенциала, заканчиваются на минимумах потенциала в этом же полотне. Минимумы и максимумы потенциала отдалены друг от друга на половину длины волны в полотне.
Как раз на этом принципе работают коллинеарные антенны из коаксиальных кабелей. Если хотите, могу сделать отдельный ролик про такие антенны.
Зависит ли волновое сопротивление полотна от параметров сигнала? Например от частоты, амплитуды, формы импульса? Конечно же нет. Волновое сопротивление полотна зависит исключительно от его погонных характеристик, от ёмкости на единицу длины и от индуктивности на единицу длины.
Но от параметров сигнала, частоты, амплитуды и формы импульса зависят такие параметры как S11, коэффициент отражения, коэффициент стоячей волны для этого сигнала в полотне, и так дальше. В один и тот же отрезок полотна можно подать сигнал, четверть длины волны которого будет совпадать с длиной отрезка полотна, а можно подать сигнал, половина длины волны которого будет совпадать с длиной отрезка. Отрезок один и тот же, и погонные характеристики у него неизменны. Но в одном случае у нас устанавливается стоячая волна с минимумом напряжения на входе, а в другом случае с максимумом напряжения на входе. Соответственно в одном случае коэффициент отражения нулевой, в другом случае полный. И КСВ тоже, в одном случае максимальный, в другом случае минимальный.
1. Волновое сопротивление любой линии измеряется как отношение приложенного к линии напряжения к току, установившемуся в этой линии под действием этого напряжения.
2. Волновое сопротивление любой линии зависит от её погонных параметров, от погонных индуктивности и емкости. Следовательно, волновое сопротивление полотна может варьироваться в широчайших пределах, его можно сделать грандиозно большим, либо грандиозно малым как у диполя Надененко.
3. Волновое сопротивление полотна и его погонные характеристики никак не зависят от параметров сигнала.
4. Но величины, связанные с самим сигналом, разумеется, зависят от параметров сигнала. S11, КСВ и т.д. зависят от формы импульсов, частоты сигнала и других параметров.
На этом заканчиваю. Если ролик был для вас полезен, ставьте лайк. Задавайте вопросы и пишите предложения в комментариях, делитесь с друзьями. И до встречи в следующих роликах!
One Response to “Волновое сопротивление антенн”
Привет, посмотрел много твоих уроков,но вот не увидел такой момент: расчет цепи согласования для антенн. Где можно найти такую информацию или может у вас есть такой урок?
Как узнать волновое сопротивление антенны

▪ Все статьи А-Я
▪ Энциклопедия радиоэлектроники и электротехники
▪ Новости науки и техники
▪ Архив статей и поиск
▪ Ваши истории из жизни
▪ На досуге
▪ Случайные статьи
▪ Отзывы о сайте

▪ Схемы и сервис-мануалы
▪ Книги, журналы, сборники
▪ Справочники
▪ Параметры радиодеталей
▪ Прошивки
▪ Инструкции по эксплуатации
▪ Энциклопедия радиоэлектроники и электротехники

(500000 статей в Архиве)


▪ Ваши истории
▪ Викторина онлайн
▪ Загадки для взрослых и детей
▪ Знаете ли Вы, что.
▪ Зрительные иллюзии
▪ Веселые задачки
▪ Каталог Вивасан
▪ Палиндромы
▪ Сборка кубика Рубика
▪ Форумы
▪ Голосования
▪ Карта сайта
Дизайн и поддержка:
Александр Кузнецов
Техническое обеспечение:
Михаил Булах
Программирование:
Данил Мончукин
Маркетинг:
Татьяна Анастасьева
При использовании материалов сайта обязательна ссылка на https://www.diagram.com.ua

сделано в Украине
Измерить параметры антенны? Совсем несложно!
Измерение сопротивления потерь. Понадобятся ферритовый стержень от магнитной антенны с парой катушек, желательно ДВ и СВ диапазонов, переменный резистор сопротивлением 0,47. 1 кОм (обязательно непроволочный), любой германиевый маломощный высокочастотный диод и вольтметр постоянного тока с высоким внутренним входным сопротивлением (не менее 0,5. 1 МОм). Для идентификации принимаемых радиостанций «на слух» полезно иметь и высокоомные телефоны.
Собираем устройство по схеме рис. 1 и, перемещая стержень в катушке магнитной антенны, настраиваемся на частоту сигнала мощной местной радиостанции.

Рис. 1
Переменный резистор R1 при этом надо установить в положение нулевого сопротивления (переместить движок в верхнее по схеме положение). Момент точной настройки контура в резонанс с частотой радиостанции будет отмечен максимальным отклонением стрелки измерителя и наибольшей громкостью в телефонах. Включенные последовательно с вольтметром телефоны практически не влияют на его показания, в то же время громкость не слишком велика. Для ее увеличения на время идентификации радиостанции вольтметр можно замкнуть, переключить на низший предел измерения, где его сопротивление меньше, или включить параллельно вольтметру конденсатор емкостью порядка 0,05. 0,1 мкФ, чтобы пропустить к телефонам звуковые частоты (при включении такого конденсатора звук может несколько исказиться из-за неравенства нагрузки детектора на звуковых частотах и на постоянном токе).
Отметив показания вольтметра (U1) и не изменяя настройки контура, движок переменного резистора R1 переместить до тех пор, пока показания вольтметра не уменьшатся вдвое (U2). При этом сопротивление резистора будет равно сопротивлению потерь антенной системы на данной частоте. Те же измерения можно провести и на других частотах.
Сопротивление резистора измеряют омметром, отключив его от измерительной цепи. При отсутствии омметра надо оснастить резистор ручкой с визиром и шкалой, которую проградуировать в омах по образцовому прибору.
Пользуясь приведенной методикой, удается выбрать, например, наилучший вариант заземления. В городских условиях возможны такие варианты: трубы водопровода, трубы отопления, арматура ограждения балкона и т. д., а также различные их сочетания. Ориентироваться следует на максимальный принимаемый сигнал и минимальное сопротивление потерь. В загородном доме, кроме «классического» заземления, рекомендуется попробовать водозаборную скважину или трубы водопровода, металлическую сетку-ограду, крышу из оцинкованной жести или любой другой массивный металлический предмет, даже если он и не имеет контакта с настоящей землей.
Измерение емкости антенны. Вместо переменного резистора теперь понадобится включить КПЕ (любого типа) с максимальной емкостью 180. 510 пФ. Желательно иметь еще и измеритель емкости с пределом измерения десятки-сотни пикофарад. Автор пользовался цифровым измерителем емкости «Мастер-С» [2], любезно предоставленным его конструктором.

Рис. 2
Если роторные пластины имеют полукруглую форму (прямоемкостный конденсатор), шкала получается линейной и тогда не надо делать чертежей и считать площади. Например, КПЕ с твердым диэлектриком из набора для детского творчества имеет максимальную емкость 180 пФ. Достаточно разбить шкалу на 18 секторов по 10 градусов, и поставить около делений 10, 20 пФ и т. д. Пусть точность будет и невысокой, для наших целей ее достаточно.
Отградуировав КПЕ, собираем установку по схеме рис. 3.

Рис. 3
Подключив антенну к гнезду XS1 и отключив КПЕ переключателем SA1, настраиваем контур, образованный емкостью антенны и катушкой L1 на частоту радиостанции. Не трогая больше катушку, переключаем антенну в гнездо XS2 и подключаем к контуру конденсатор С2 (наш КПЕ) переключателем SA1. Снова настраиваемся на ту же частоту, теперь уже С помощью С2. Определяем его емкость Ск по шкале или с помощью измерителя емкости, подключенного к гнездам XS3, XS4 (переключив для этого SA1 в показанное на схеме положение). Осталось найти емкость антенны СА по формуле
СА = С2(1 + sqrt(1 +4С1/С2))/2.
Смысл наших манипуляций в следующем: когда мы подключили антенну через конденсатор связи С1, общая емкость контура стала меньше, и чтобы ее восстановить, пришлось добавить емкость С2. Вы и сами можете вывести приведенную формулу исходя из равенства емкости антенны СА (в первом случае) и сложной контурной емкости С2 + САС1/(СА + С1) во втором случае. Для повышения точности измерений емкость конденсатора связи желательно выбирать поменьше, в пределах 15. 50 пФ. Если емкость конденсатора связи намного меньше емкости антенны, то и расчетная формула упрощается:
Эксперимент и его обсуждение. Автор измерял параметры имевшейся на даче антенны такого вида: провод ПЭЛ 0,7 длиной 15 м, который протянут к коньку крыши и в сторону от дома к соседнему дереву. Наилучшим «заземлением» (противовесом) оказалась изолированная от земли водонагревательная колонка с небольшой сетью труб и батарей местного отопления. Все измерения проведены в СВ диапазоне с использованием стандартной СВ катушки магнитной антенны от транзисторного приемника. Если для настройки на низкочастотном краю диапазона индуктивности не хватало, рядом с магнитной антенной помещался еще один ферритовый стержень, параллельно первому.
Результаты измерений сведены в таблицу. Они нуждаются в небольших комментариях. Прежде всего, бросается в глаза, что на разных частотах и сопротивление потерь и емкость антенны разные. Это вовсе не ошибки измерений. Рассмотрим сначала частотную зависимость емкости. Если бы провод антенны не обладал еще и некоторой индуктивностью LА значения емкости были бы одинаковыми. Индуктивность провода включена последовательно с емкостью антенны, как видно из эквивалентной схемы антенной цепи, показанной на рис. 4.

Рис. 4
В связи с этим многие данные, полученные радиолюбителями при измерении параметров своих антенн, могут оказаться весьма полезными.


Проектирование и анализ директорной антенны
Два японских профессора Уда и Яги придумали и изучили эту антенну еще в 1920-х годах. Первую такую антенну построил С. Уда и в 1926 и 1927 годах опубликовал результаты в Японии [1]. Годом позже проект получил дальнейшее развитие, и был опубликован его коллегой профессором Яги на английском языке [2]. С тех пор инженерами и энтузиастами был выполнен существенный объем теоретической и главным образом экспериментальной работы. Стало доступно огромное количество их данных и результатов.
Существенной особенностью этого типа антенны, является то, что при изменении ее положения в пространстве она обладает практически неизменными параметрами и, кроме того, ее характеристики не зависят от погодных явлений. Как показано на рис. 1, данная антенна состоит из трех различных элементов: ведомого элемента, рефлектора (одного или нескольких) и директора (одного или нескольких).
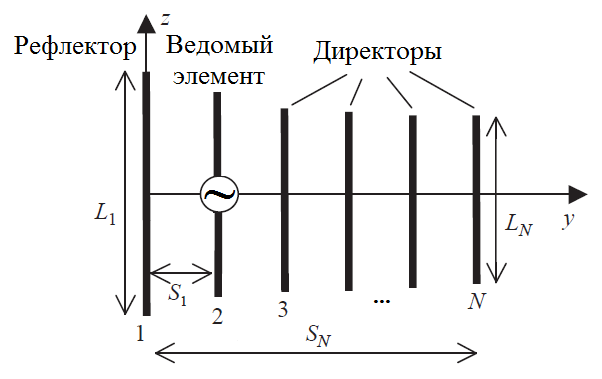
Рис.1 Директорная антенна
Часто эту антенну рассматривают как массив (антенную решетку), поскольку она состоит из нескольких элементов. Однако запитываемым – активным элементом антенны является только один ведомый элемент. Все остальные элементы антенны (рефлектор и директор) являются пассивными – паразитными элементами, поэтому чаще всего их рассматривают не в качестве элементов массива, а в качестве элементов собственно антенны. Основные характеристики этих элементов и рекомендации по их проектированию могут быть сведены к следующему:
1. Продольные размеры первых трех элементов антенны изменяются от длинного к короткому и связаны логарифмически:
где τ – некоторая постоянная близкая к единице (τ ≈ 0,83 ÷ 0,96).
У некоторых многоэлементных антенн продольные размеры нескольких последних директоров или даже всех директоров, могут быть одинаковыми.
2. Ведомый элемент определяет поляризацию и центральную частоту антенны. В случае полуволнового диполя его рекомендуемая длина составляет около 0,475λ. Полуволновой диполь хорошо согласуется с питающим фидером с волновым сопротивлением 50 или 75 Ом.
3. Рефлектор перенаправляет излученную энергию вперед в сторону ведомого элемента. Длина рефлектора примерно на 5% больше размера ведомого элемента антенны. Его сопротивление носит индуктивный характер. Было установлено, что добавление большего числа рефлекторов не приводит к значительным улучшениям, поэтому чаще всего в антенне один рефлектор. Оптимальное расстояние между рефлектором и ведомым элементом находится между 0,1λ и 0,25λ. Длина рефлектора сильно влияет на относительный уровень заднего излучения и входное сопротивление антенны.
4. Директор направляет излученную энергию вперед в сторону противоположную ведомому элементу и рефлектору. Длина директора примерно на 5% меньше размера ведомого элемента антенны. Его сопротивление носит емкостной характер. Количество директоров определяет максимально достижимую направленность и усиление антенны. Однако при увеличении числа директоров более 12, эффект от количества директоров на направленность антенны значительно падает и, кроме того, резко снижается входное сопротивление антенны. Поэтому при большом количестве директоров в качестве ведомого элемента, как правило, используется петлевой вибратор (вибратор Пистолькорса). Оптимальное расстояние между директорами находится между 0,1λ и 0,35λ. У более длинных массивов интервал больше, у более коротких массивов интервал меньше.
5. Поперечный размер элементов антенны, диаметр их трубок или ширина их полос, находится между 0,01λ и 0,001λ. Поперечный размер элементов оказывает значительное влияние на входное сопротивление антенны.
Регулируя расстояния между элементами антенны и изменяя их размеры можно управлять полосой пропускания, формой и шириной образца излучения антенны. Полный образец излучения антенны формируют: направленное усиление, отношение усиления в направлении приема к усилению в противоположном направлении, ширина луча и нежелательный уровень боковых лепестков.
Выбор разнообразных целей, которые можно преследовать при проектировании антенны, является субъективным, и ограничения, накладываемые этим выбором, являются главным образом вопросом выбора разработчика, что и объясняет наличие огромного числа различного рода рекомендаций и методик по проектированию таких антенн.
В этих условиях большое значение приобретает возможность быстрой оценки влияния результатов небольшой модификации расчетной геометрии антенны на полный образец ее излучения. Эта возможность позволяет получить хорошее понимание не только потенциала выбранных рекомендаций и методов проектирования, но и самой проектируемой антенны.
Наиболее удобно такая возможность реализуется с помощью компьютерной программы работающей в диалоговом режиме, когда разработчик может внести некоторые изменения и сразу увидеть, как эти изменения отразились на результате.
Подобная программа анализа директорной антенны реализована в математическом пакете «Mathcad» организованном по принципу What You See Is What You Get (англ. – то, что Вы видите, то Вы и получите). Отличительной особенностью таких программ является то, что их язык максимально приближен к знакомому еще со средней школы обычному языку символьной математики, и освоение такого языка программирования происходит весьма просто и почти на интуитивном уровне. Программа работает в пакетах Mathcad версий 11 и выше.
Исходными данными для расчета и анализа параметров антенны являются: рабочая частота антенны, волновое сопротивление фидера, напряжение на входных выводах ведущего элемента (для удобства сравнения антенн разных типов, это напряжение следует выбирать так, чтобы оно обеспечивало ток ведущего элемента близкий к одному амперу), расстояние от антенны до точки наблюдения (расстояние до дальней зоны антенны), общее число элементов антенны, число рефлекторных элементов, число директорных элементов.
Программа сама рассчитает предварительную геометрию антенны, однако эта геометрия будет оптимизирована под оптимальное волновое сопротивление питающего фидера. Если же следует выполнить анализ характеристик антенны рассчитанной по другим методикам или антенны с уже известной геометрией, необходимо сразу ввести известную геометрию антенны в разделе “Описание геометрии антенны”, заменив вычисленные программой данные на требуемые.
Для описания геометрии антенны в программе используются одномерные массивы в виде вектора. Если, например, требуется ввести сведения о размерах длин элементов, то ввод значений вектора осуществляется следующим образом:
1. Ввод начинают с наиболее удаленного рефлектора, двигаясь внутрь к ведущему элементу. После ввода длины и радиуса ведущего элемента вводят параметры директорных элементов, начиная с директора, следующего сразу за ведущим элементом, двигаясь наружу к последнему элементу.
2. Численное значение размера очередного элемента вводят через запятую.
3. Дробная часть численного значения отделяется от целой части не запятой, а точкой.
Результат таких действий после ввода размеров рефлектора, ведомого элемента и первого директора показан на рис. 2.
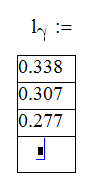
Рис. 2 Ввод длины элементов антенны
По введенным входным величинам будут вычислены следующие характеристики антенны: максимальная интенсивность излучения, излучаемая антенной мощность, сопротивление излучения, коэффициент направленного действия антенны, эффективная изотропная излучаемая мощность, коэффициент отражения по напряжению в питающем фидере, коэффициент стоячей волны напряжения в питающем фидере, отражающая эффективность системы фидер – антенна, максимальная эффективная площадь антенны, максимальная эффективная высота антенны. Будут вычислены и некоторые другие второстепенные величины, которые могут представлять для разработчика тот или иной интерес. Для удобства блоки Mathcad вычисляемых величин выделены желтым цветом, а две вычисляемые характеристики, значения которых важны при ручной оптимизации антенны, выделены голубым цветом.
По умолчанию в качестве ведомого вибратора антенны в программе рассматривается полуволновой диполь. Однако если требуется выполнить вычисления характеристик антенны использующей в качестве ведомого петлевой вибратор, необходимо в разделе “Анализ параметров антенны” включить блок вычисления собственного импеданса петлевого вибратора. Для этого необходимо поместить курсор на изображение данного выражения, и нажав правую кнопку мыши, в появившемся контекстном меню выбрать пункт “Включить вычисление”, так, как это показано на рис.3.
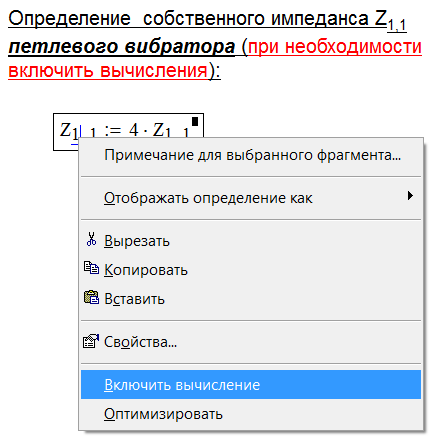
Рис. 3 Включение вычислений определения собственного импеданса петлевого вибратора
Кроме того, для того чтобы подпрограмма расчета АЧХ антенны также выполняла вычисления АЧХ антенны использующей в качестве ведомого петлевой вибратор, необходимо в разделе “Построение амплитудно-частотной характеристики антенны” заменить значение переменной FD на единицу.
Переменные “Director”, “Reflector,” “Diameter” и “Frequency” позволяют в режиме реального времени выполнять модификации расчетной или исходной геометрии антенны и наблюдать влияние этих модификаций на полный образец излучения антенны и ее АЧХ. Для удобства блоки Mathcad этих переменных выделены зеленым цветом.
В заключение отметим, что использование компьютеризированного подхода к расчету и анализу директорных антенн дает несколько значительных преимуществ перед экспериментальным подходом. Среди таких преимуществ очевидная экономия времени и денег, а также возможность получения конструкций антенн оптимизированных относительно одного или даже нескольких желаемых параметров, таких как направленность, уровень боковых лепестков, ширина полосы пропускания и других.
Программа находится в прикрепленном архиве.
1. S. Uda, “Wireless beam of short electric waves,” J. IEE (Japan), 1926, March, pp. 273-282 и 1927, November, pp. 1209-1219.
2. Yagi, H., “Beam Transmission of Ultra-short Waves,” Proc. IRE, 1928, vol. 16, no. 6, pp. 715–740.
3. Thomas A. Milligan, “Modern Antenna Design”, John Wiley & Sons, Inc., Hoboken, New Jersey, 2005.
М. Агунов, Н. Вербова, г. Санкт-Петербург