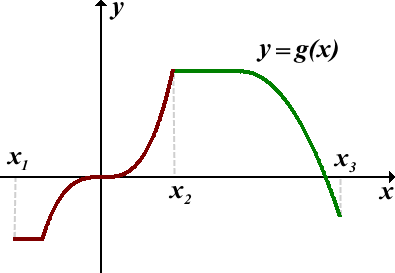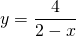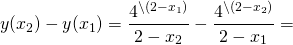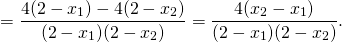как узнать возрастающая или убывающая функция
Возрастание и убывание функций
1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
x_1 \Rightarrow f(x_2 ) > f(x_1 ). \]» title=»Rendered by QuickLaTeX.com»/>
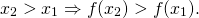
2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
x_1 \Rightarrow f(x_2 )
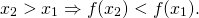
Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.
График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).
На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).
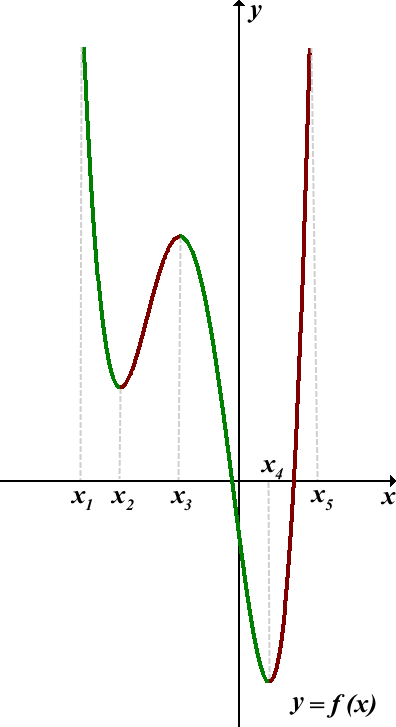
Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x1;x5]:
Кратко это записывают так:
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).
4) Если функция возрастает на всей своей области определения, то её называют возрастающей.
Если функция убывает на всей своей области определения, то её называют убывающей.
Например, y=√x, y=x³ — возрастающие функции.
Линейная функция y=kx+b возрастающая при k>0 и убывающая при k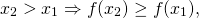 
x_1 \Rightarrow f(x_2 ) \ge f(x_1 ), \]» title=»Rendered by QuickLaTeX.com»/>
то функция y=f(x) называется неубывающей на этом промежутке.
6) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
x_1 \Rightarrow f(x_2 ) \le f(x_1 ), \]» title=»Rendered by QuickLaTeX.com»/>
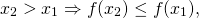
то функция y=f(x) называется невозрастающей на этом промежутке.
7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.
Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x1;x3], является невозрастающей и неубывающей:
Функция y=g(x) является неубывающей на промежутке [x1;x2].
Функция y=g(x) является невозрастающей на промежутке [x2;x3].
Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.
Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?
группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:
Теперь выносим общий множитель (x2-x1) за скобки:
Так как x2>x1, то x2-x1>0. Следовательно, знак произведения зависит от знака второго множителя.
Для x1, x2 ∈(-∞;-2) x2+x1+4 
возрастает на промежутке (2;+∞).
Функция определена при x∈(-∞;2) и (2;+∞).
0. \]» title=»Rendered by QuickLaTeX.com»/>
Отсюда y(x2)-y(x1)>0. Поэтому данная функция возрастает на промежутке (2;+∞).
Что и требовалось доказать.
Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Возрастание и убывание функции
Общие понятия о поведении функций
Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.
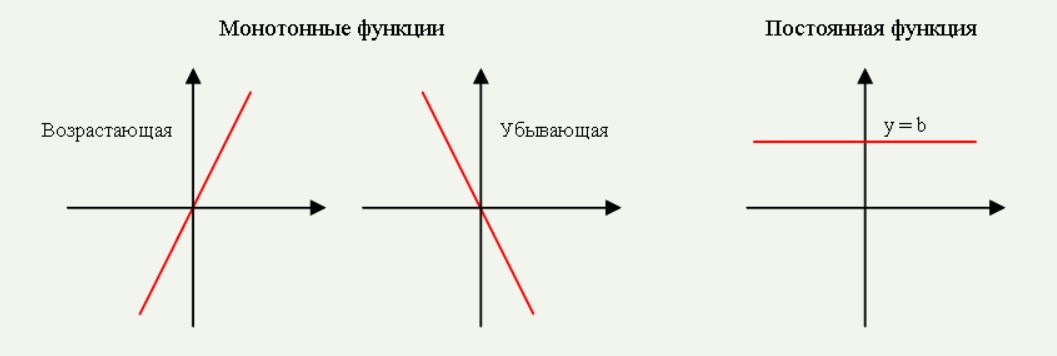
Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.
Соответственно, монотонная функция может быть возрастающая или убывающая.
Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.
Математическое выражение этого определения выглядит следующим образом:
Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.
Математическое выражение этого определения выглядит следующим образом:
Разберем примеры решения задач на изучение характера поведения функции.
Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.
Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.
Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.
Не нашли что искали?
Просто напиши и мы поможем
Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.
Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.
То есть функция \(y=5\) будет постоянной.
Постоянная, не убывающая и не возрастающая функции не есть монотонные.
Свойства монотонных функций
К свойствам монотонных функций относятся такие характеристики:
Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Точки экстремума, экстремумы функции
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Иначе говоря, получим их условия постановки знака:
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
После чего необходимо найти производную:
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
Перейдем к вычислению минимумов:
Произведем вычисления максимумов функции. Получим, что
Второй признак экстремума функции
Для начала находим область определения. Получаем, что
Необходимо продифференцировать функцию, после чего получим
Третье достаточное условие экстремума
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Возрастание и убывание функции
Что такое возрастающие и убывающие функции
Монотонная функция — функция, изменяющаяся исключительно в одном и том же направлении.
И убывающая, и возрастающая функции относятся именно к понятию монотонной.
Возрастающая функция — линейная функция, возрастающая при увеличении значения аргумента.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Убывающая функция — линейная функция, убывающая при увеличении значения аргумента.
Также важно знать, что существует постоянная функция, значение которой не меняется на всем промежутке графика.
Свойства и признаки, пример
Достаточными условиями для возрастания или убывания функций являются следующие признаки:
Кроме этого, у монотонных функций есть характерные особенности, называемые свойствами. Они помогают в решении задач различной сложности: начиная от функций с логарифмами и заканчивая неравенствами с функциями. Свойства:
Рассмотрим пример-доказательство для убывающей функции:
Возьмем точки x1 и x2, чтобы \(0\leq x_1\leq x_2.\) Посмотрим на разность значений функции в данных точках.
Возрастающими являются также следующие функции: