как узнать высоту прямоугольного параллелепипеда

Прямоугольный параллелепипед. Что это такое?

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

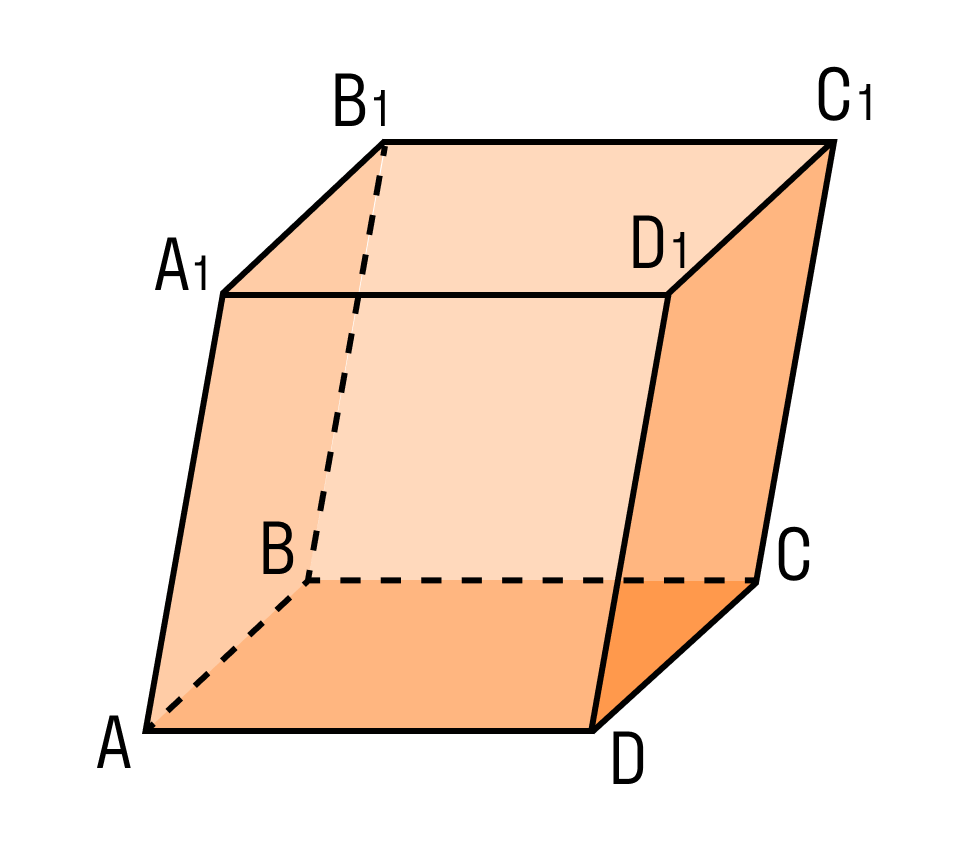
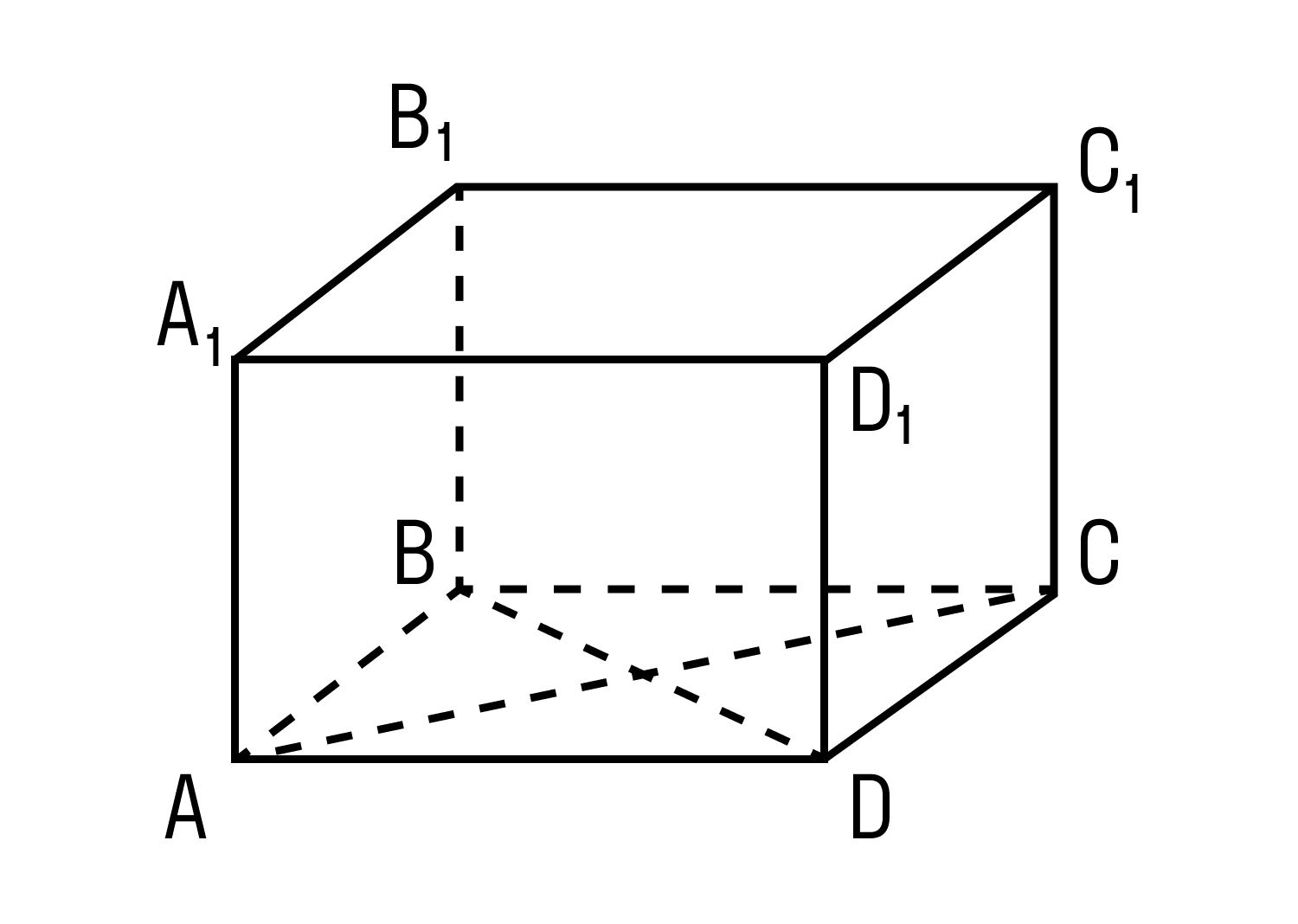
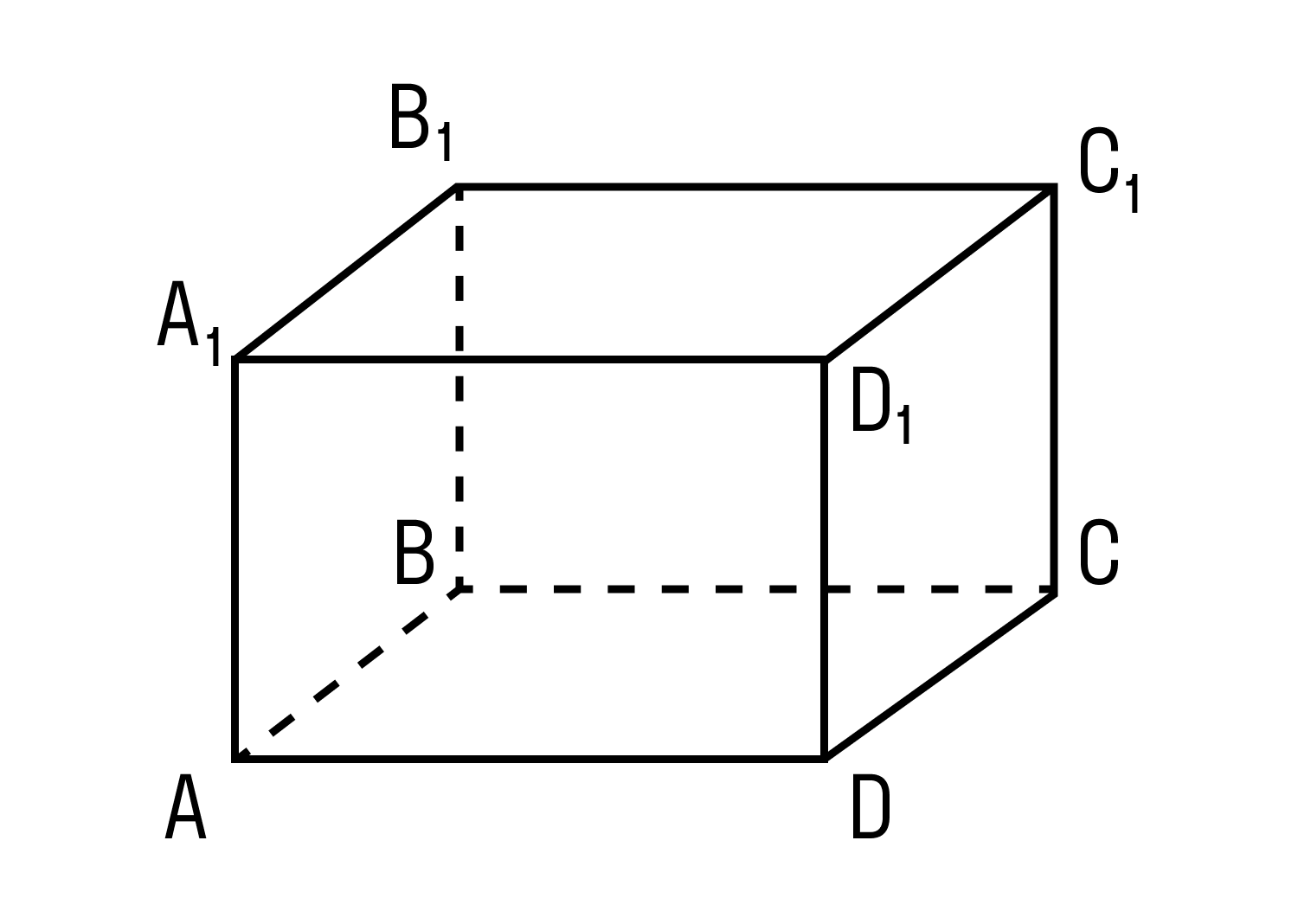
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

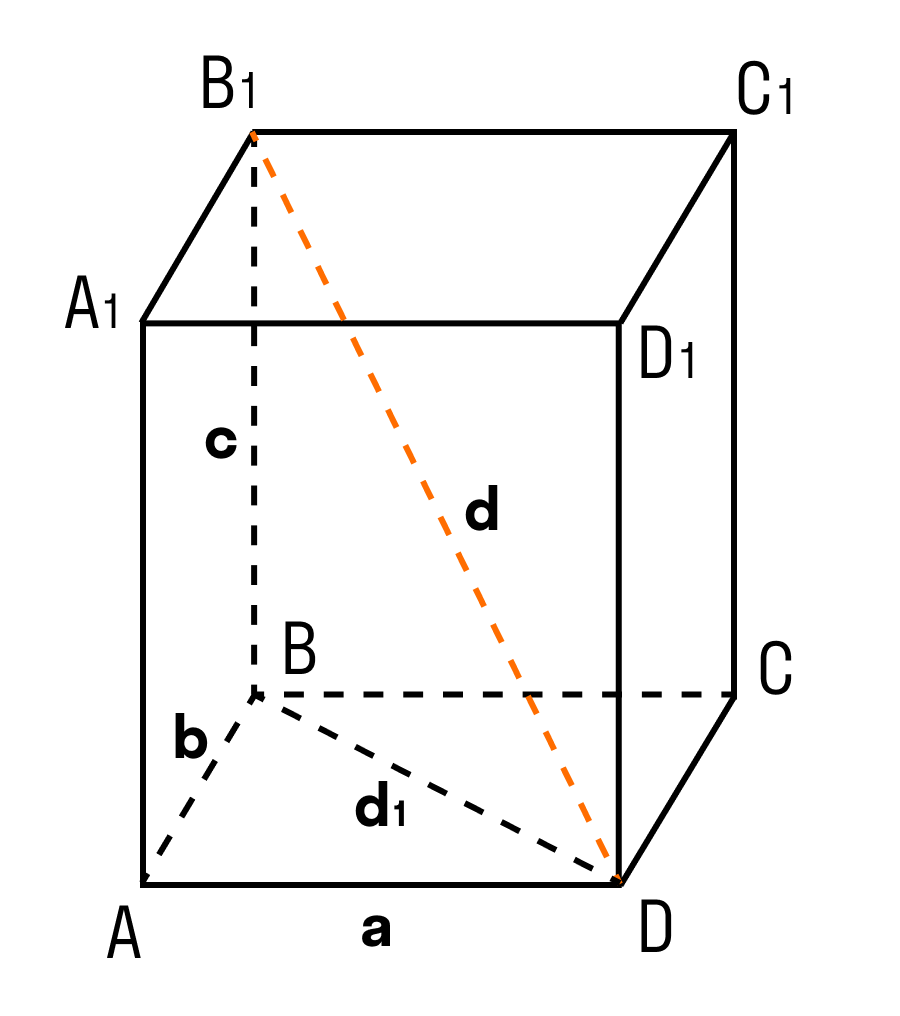
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

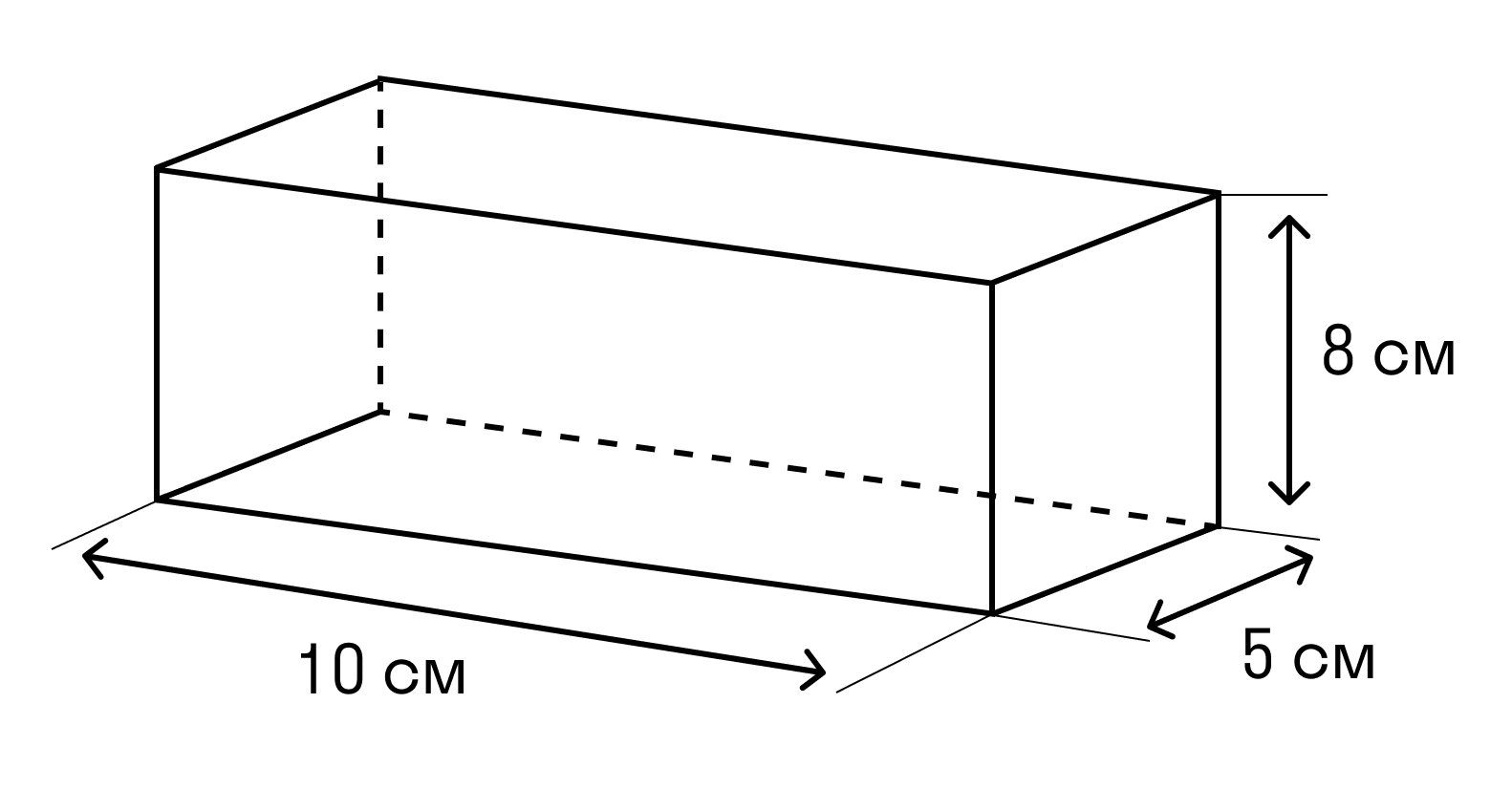
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

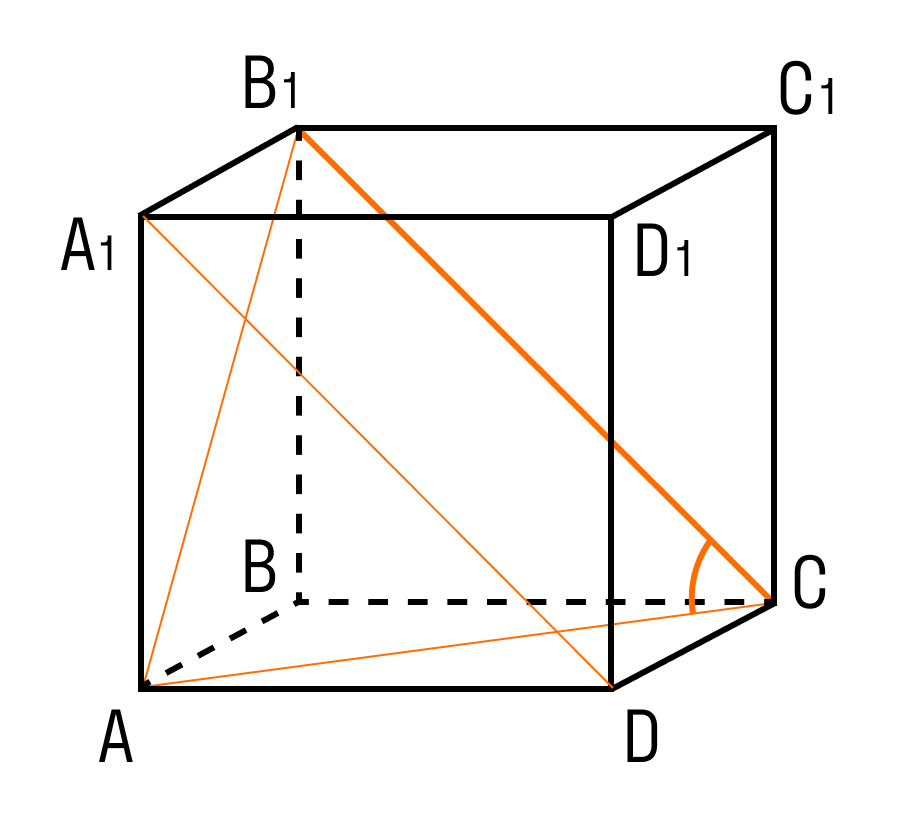
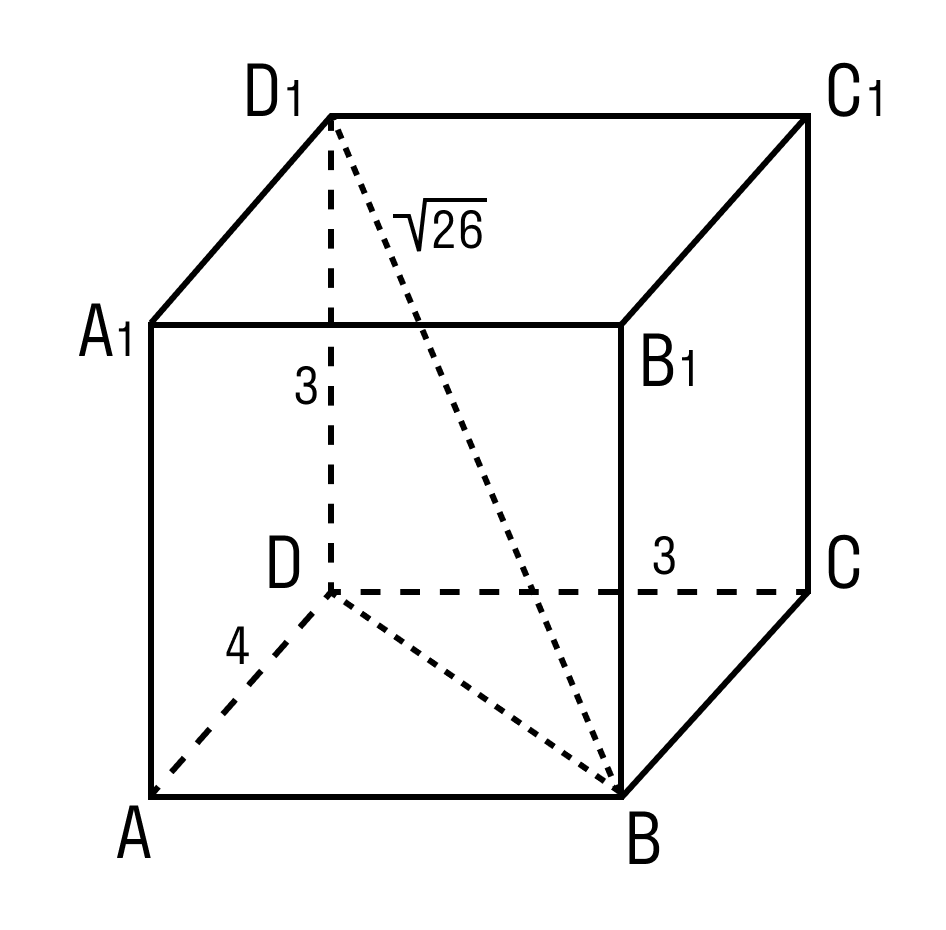
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

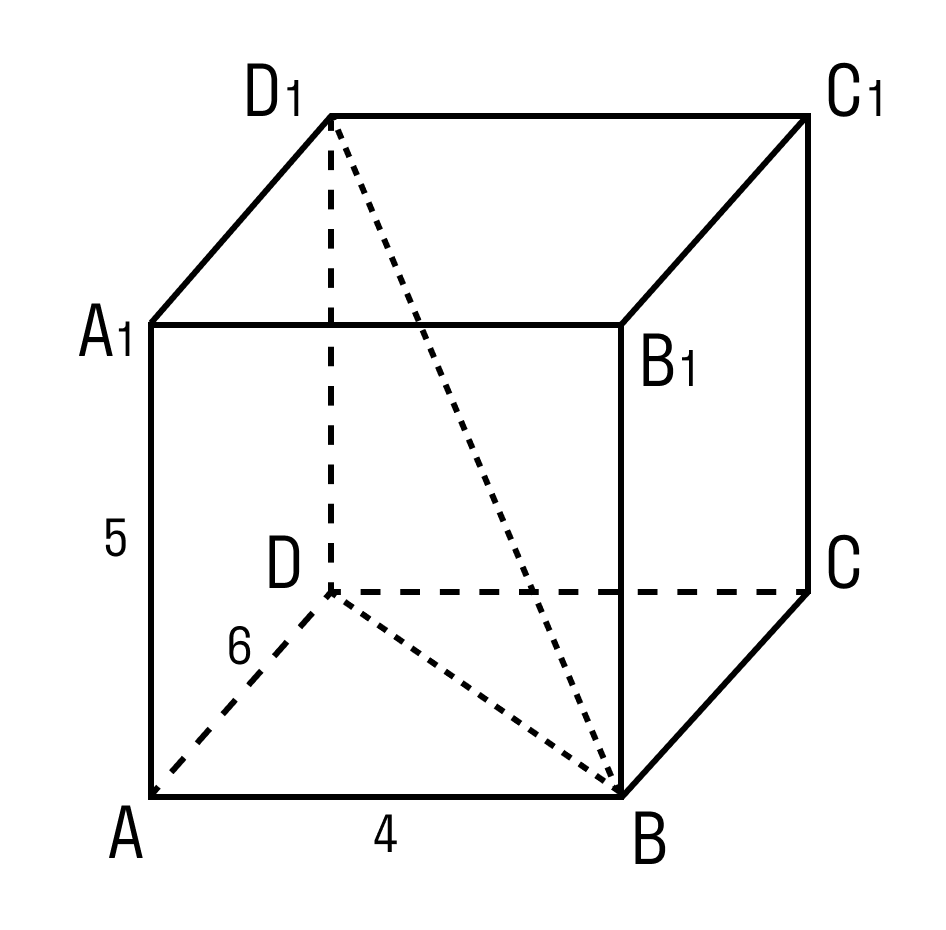
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

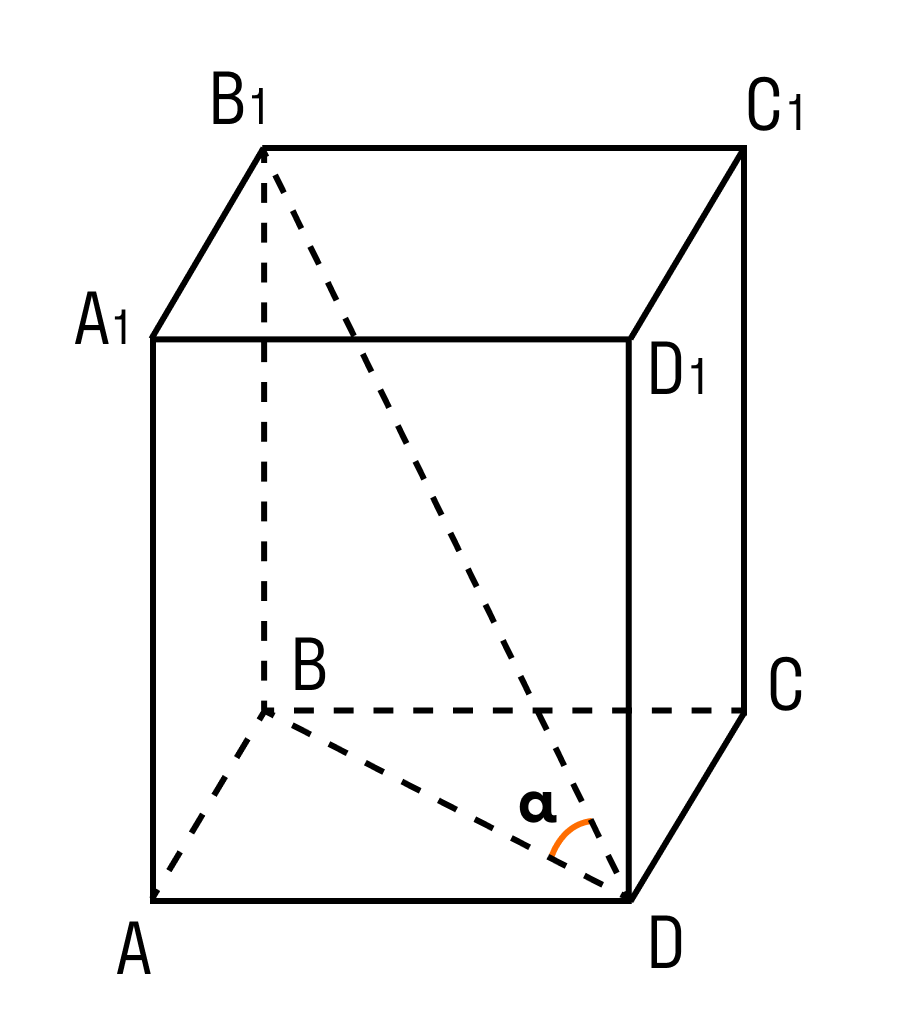
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник

Объем параллелепипеда

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения объема (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, вина в бочке, земли в клумбе.

Два свойства объёма

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

Давайте вспомним, какие виды параллелепипедов бывают.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань которой называется параллелограмм.

Призма — это многогранник, в основаниях которого лежат равные многоугольники, а его боковые грани — это параллелограммы.

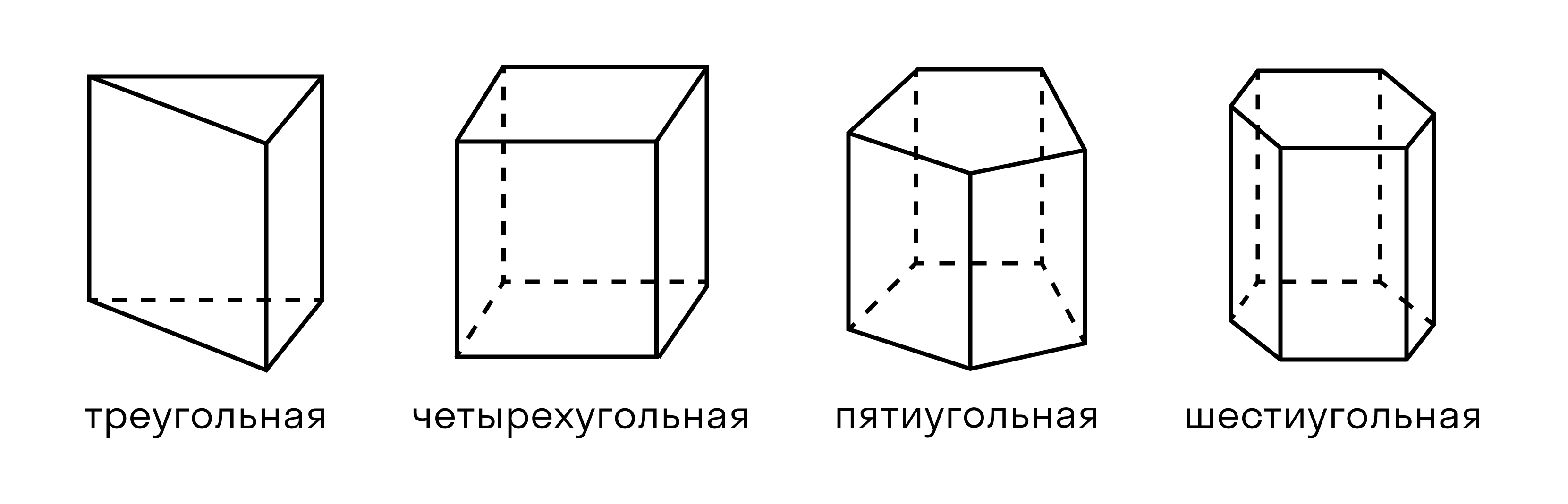
Какие бывают призмы:

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a * b * h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

Источник

Как найти высоту прямоугольного параллелепипеда?

Как найти высоту прямоугольного параллелепипеда?

В категории Образование Спросил Gavijurus

1 Ответ 2233 Просмотров 1 месяц назад

Для добавления вопроса на сайт, блог или форум просто скопируйте и вставьте в html код:

Для ответа на вопрос, как найти высоту прямоугольного параллелепипеда, необходимо сначала уяснить себе, что такое прямоугольный параллелепипед.

Прямоугольный параллелепипед это объемная геометрическая фигура, имеющая шесть граней, восемь углов и двенадцать ребер. Все углы прямоугольного параллелепипеда прямые, откуда и появилось название, то есть все углы равны девяноста градусам. Для того, чтобы представить себе эту геометрическую фигуру, достаточно представить себе кирпич.

Частным случаем прямоугольного параллелепипеда является случай, когда все ребра равны между собой. В этом случае фигура будет называться кубом.

Для нахождения высоты прямоугольного параллелепипеда необходимо знать значение некоторых его элементов. Значение высоты присутствует, например, в определении объема прямоугольного параллелепипеда. Чтобы определить объем, необходимо знать длину и ширину основания, перемножить их между собой, а затем умножить на высоту.

Таким образом получим величину объема прямоугольного параллелепипеда.

Исходя из этого, для нахождения высоты прямоугольного параллелепипеда необходимо величину его объема разделить на площадь основания.

Для примера возьмем прямоугольный параллелепипед, длина равна 6 сантиметров, ширина равна 5 сантиметров, а объем равен 90 кубическим сантиметрам. Сначала вычислим площадь основания, умножив 5 на6 сантиметров. получим 30 квадратных сантиметров.

Разделив 90 куб. см на 30 кв.см, получим что высота равна 3 см.

Источник

Как найти высоту прямоугольного параллелепипеда формула?

V= S*h. — основная формула, из нее можно вывести высоту. V- объем. S(осн) — Площадь основания.

Как найти высоту прямоугольного параллелепипеда если известны стороны основания?

Ответ, проверенный экспертом

Как найти высоту прямоугольного параллелепипеда если известен его объем?

Как найти высоту если известен объём, длина и ширина

объём разделить на произведение длины на ширину т. е. apsiganocj и 337 других пользователей посчитали ответ полезным!

Как найти высоту прямоугольного параллелепипеда если известна площадь?

чтобы найти высоту надо длина + ширина. Потом площадь : длина + ширина.

Как найти высоту по объему?

Как найти высоту комнаты зная объём и площадь

Объем делишь на площадь и получаешь высоту.

Как найти высоту прямоугольного?

Примеры решения задач

Куда падает Высота наклонного параллелепипеда?

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, относительно оснований, под не прямым углом. Наклонная призма эквивалентна такой прямой призме, у которой основание равняется перпендикулярному сечению наклонной призмы, а высота — ее боковому ребру.

Как найти высоту в ромбе?

Как найти высоту ромба. Формулы

Как найти площадь поверхности прямоугольного параллелепипеда если известен объем?

S=18·7=126 (см2) – площадь прямоугольника. Чтобы узнать ОБЪЕМ прямоугольного параллелепипеда нужно длину а умножить на ширину b и полученное произведение умножить на высоту с.

Как найти высоту если известен радиус?

Рассмотрим формулу, с помощью которой можно найти высоту: V=πR^2*H, где R – радиус основания цилиндра, H – искомая высота.

Как найти объем параллелепипеда если известна площадь?

Объем любого параллелепипеда равняется произведению площади его основания на высоту.

Как найти высоту параллелепипеда Зная длину и ширину?

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту: V = S*h. Поскольку в основании параллелепипеда лежит прямоугольник, площадь этого основания равна S=a*b, где a — длина, b — ширина. Отсюда, объем равен V=a*b*h, где h — высота (причем, h = c, где c — ребро параллелепипеда).

Как найти высоту в кубе?

Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.

Как узнать высоту зная площадь?

Подставьте данные вам значения в формулу для вычисления площади (А = 1/2bh) и найдите высоту. Сначала умножьте сторону (b) на 1/2, а затем разделите площадь (А) на полученное значение. Таким образом, вы найдете высоту треугольника.

Как из объема цилиндра найти высоту?

Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.
…
Расшифровать формулу просто:

Как найти высоту в пирамиде?

Как найти высоту пирамиды, если известен ее объем

Через формулу V = (S*h)/3 (в формуле V — объем, S — площадь основания, h — высота пирамиды) находим, что h = (3*V)/S.

Источник

Объемы фигур. Объем параллелепипеда.

Объем прямоугольного параллелепипеда, формула.

Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда

6 граней, а они, в свою очередь, являются параллелограммами.

Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.

Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

a – длина параллелепипеда,

b – ширина параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница

Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями

прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это

Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.

Объем прямого параллелепипеда, формула.

Как найти объем параллелепипеда?

Площадь боковой поверхности параллелепипеда, формула:

где Р_о — периметр основания,

Площадь полной поверхности, формула

где S_о — площадь основания

Формула объёма прямого параллелепипеда:

Объем произвольного параллелепипеда.

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного

произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят

Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель

Грама указанных 3х векторов равен квадрату их смешанного произведения.

Источник