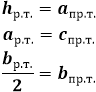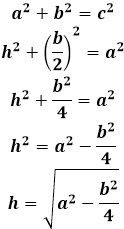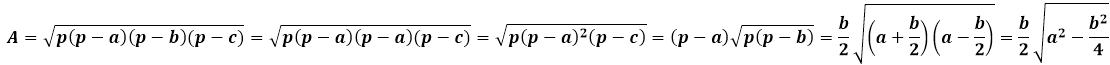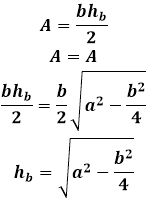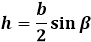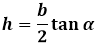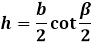как узнать высоту равнобедренного треугольника

Равнобедренный треугольник: свойства, признаки и формулы

Содержание:

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника

Доказательство теоремы:

Вывод:

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

Доказательство теоремы:

Доказательство от противного.

Признаки равнобедренного треугольника

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

Формулы длины стороны (основания — b):

Формулы длины равных сторон — (а):

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

Формула высоты, биссектрисы и медианы, через стороны, (L):

Площадь равнобедренного треугольника

Формула площади треугольника через высоту h и основание b, (S):

Источник

Высота и сторона «A» равнобедренного треугольника

Свойства

Так как высота равнобедренного треугольника, опущенная на основание, является одновременно и биссектрисой и медианой, следовательно, она делит основание и угол при вершине на две равные части, образуя прямоугольный треугольник со сторонами a и b/2. Из теоремы Пифагора в таком треугольнике можно найти само основание, а затем рассчитать все остальные возможные данные. (рис.88.2) h^2+(b/2)^2=a^2 b=√(a^2-h^2 )/2

Чтобы вычислить периметр равнобедренного треугольника, надо к двум боковым сторонам прибавить основание или приведенный выше радикал через высоту. P=2a+b=2a+√(a^2-h^2 )/2

Площадь равнобедренного треугольника через высоту и основание по определению вычисляется как половина их произведения. Заменив основание на соответствующее ему выражение, получаем площадь через высоту и боковую сторону равнобедренного треугольника. S=hb/2=(h√(a^2-h^2 ))/4

В равнобедренном треугольнике равны не только боковые стороны, но и углы при основании, а так как в сумме они дают всегда 180 градусов, то любой из углов можно найти, зная другой. Первый угол вычисляется по теореме косинусов, приведенной для равных боковых сторон, а второй можно найти через разность от 180. (рис.88.1) cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 ) α=(180°-β)/2 β=180°-2α

Центральные медиана и биссектриса, опущенные на основание совпадают с высотой, а боковые медианы, высоты и биссектрисы можно найти по следующим формулам для равнобедренных треугольников. Чтобы вычислить их через высоту и боковую сторону, нужно заменить основание на эквивалентное ему выражение. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

Высота, опущенная на боковую сторону, через высоту, опущенную на основание и боковую сторону равнобедренного треугольника. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a=(√(a^2-h^2 ) √((4a^2-a^2+h^2)))/2a=√((a^2-h^2)(3a^2+h^2))/2

Средняя линия проводится параллельно любой стороне треугольника, соединяя середины боковых в ее отношении сторон. Таким образом, она всегда оказывается равна половине параллельной ей стороны. Вместо неизвестного основания в формулу можно подставить используемый радикал, чтобы найти среднюю линию через высоту и боковую сторону равнобедренного треугольника(рис. 88.5) M_b=b/2=√(a^2-h^2 )/2 M_a=a/2

Радиус окружности, вписанной в равнобедренный треугольник, начинается от точки на пересечении биссектрис и уходит перпендикулярно в любую из сторон. Чтобы его найти через высоту и боковую сторону треугольника, надо заменить основание в формуле на радикал. (рис. 88.6) r=1/2 √(((a^2-h^2)(2a-√(a^2-h^2 )))/(2a+√(a^2-h^2 )))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы путем подстановки радикала через высоту и боковую сторону вместо основания. (рис. 88.7) R=a^2/√(3a^2-h^2 )

Источник

Высота равнобедренного треугольника

Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.

Рассмотрим каждый случай по отдельности.

Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.

Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:

Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.

Формула Герона для равнобедренного треугольника будет иметь несколько упрошенный вид за счет того, что значения боковых сторон повторяются:

Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне

Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.

Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sin⁡α

Формула через боковую сторону и угол напротив основания β:

Формула через основание и угол при нем α:

через основание и угол противолежащий ему β:

Источник

Равнобедренный треугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.

Определение равнобедренного треугольника

Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.

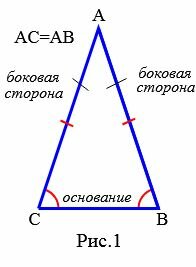
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).

Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.

Существует более общее определение равнобедненого треугольника:

Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.

Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.

Теорема о равнобедренном треугольнике

Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.

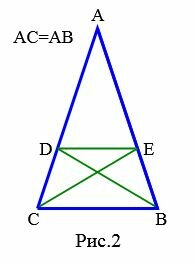Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что \( \small \angle B= \angle C. \) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол \( \small \angle A \) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:

Из \( \small AB=AC\) и \( \small AD=AE \) следует:

Из (2) и (4) следует, что \( \small \angle B= \angle C. \)

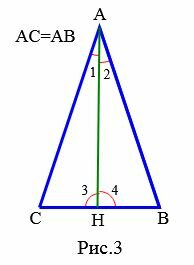Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису \( \small AH \) треугольника. Тогда \( \small \angle CAH=\angle BAH. \) Докажем, что \( \small \angle B= \angle C. \) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle CAH=\angle BAH. \) Отсюда следует: \( \small \angle B= \angle C. \)

Свойства равнобедренного треугольника

Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.

Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle 1=\angle 2. \) Тогда \( \small CH=HB, \) \( \small \angle 3=\angle 4. \) Равенство \( \small CH=HB \) означает, что \( \small AH \) является также медианой треугольника ABC. Углы \( \small \angle 3\) и \( \angle 4 \) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда \( \small AH \) является также высотой треугольника \( \small ABC. \) Поскольку высота \( \small AH \) перпендикулярна к \( \small BC \) и \( \small CH=HB, \) то \( \small AH \) является также серединным перпендикуляром к основанию равнобедренного треугольника.

Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.

Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:

Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.

Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.

Признаки равнобедренного треугольника

Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.

Признак 1 следует из определения 1.

Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.

Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).

Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

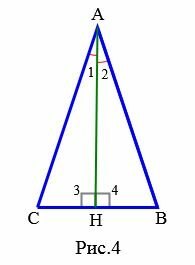
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (первый признак равенства треугольников): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)

Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)

Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

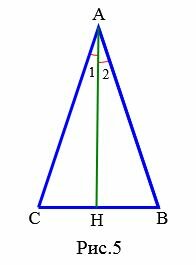
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда

Применим теорему синусов для треугольника \( \small AHC \):

Применим теорему синусов для треугольника \( \small AHB \):

тогда, из (5), (6), (7) получим:

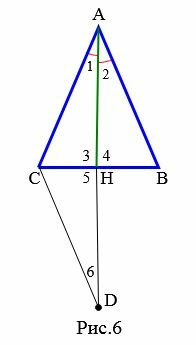Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне

Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.

Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине

Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.

Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.

3. Признак равенства равнобедренных треугольников по основанию и углу при основании

Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.

Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.

Задачи и решения

Задача 1. Известны основание \( \small a=5 \) и высота \( \small h=6 \) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.

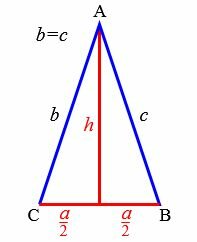Решение. Найдем боковые стороны \( \small b \) и \( \small c \) равнобедренного треугольника. Воспользуемся теоремой Пифагора:

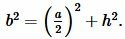Подставляя значения \( \small a \) и \( \small h \) в (9), получим:

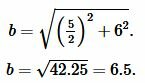Боковая сторона \( \small c \) равнобедренного треугольника равна:

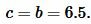Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:

Подставляя значения \( \small a=5, \) \( \small b=6.5 \) и \( \small c=6.5 \) в (10), получим:

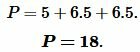Найдем угол \( \small B \) равнобедренного треугольника:

Подставляя значения \( \small a=5, \) \( \small h=6 \) в (11), получим:

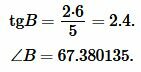Тогда угол \( \small C \) равнобедренного треугольника равен:

Поскольку сумма всех углов треугольника равна 180°, то имеем:

,

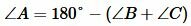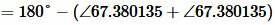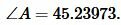Площадь треугольника можно вычислить из формулы:

Подставляя значения \( \small a=5, \) \( \small h=6 \) в (12), получим:

Источник

Стороны равнобедренного треугольника

Свойства

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

Источник