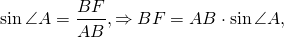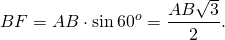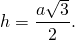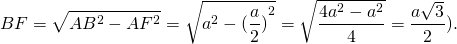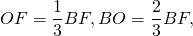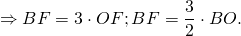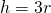как узнать высоту равностороннего треугольника
Высота равностороннего треугольника
Что такое равносторонний треугольник?
Для начала нужно вспомнить, что такое равносторонний треугольник, определить некоторые его свойства и только тогда выводить формулу высоты.
Равносторонний треугольник – это треугольник, все стороны которого равны между собой. Все углы в таком треугольнике равны между собой (60 градусов).
Рис. 1. Правильный треугольник.
Равносторонний треугольник является равнобедренным, но основанием можно считать любую часть треугольника.
Формула
Формулу высоты равностороннего треугольника выведем тремя способами: через теорему Пифагора, с помощью формулы площади прямоугольного треугольника и через тригонометрическую функцию. Три способа используем, чтобы показать несколько вариантов доказательства и иметь возможность максимально быстро найти значение высоты при любом условии задачи.
Рис. 2. Рисунок к доказательству.
Сначала выведем формулу через площадь.
Приравняем две формулы и выведем формулу высоты.
$<1\over2>*a*h=\sqrt<3>*
$H=\sqrt<3>*
С другой стороны, в равностороннем треугольнике высота, проведенная к основанию, является медианой и высотой. То есть, высоту можно найти как катет прямоугольного треугольника через теорему Пифагора.
Рис. 3. Рисунок к доказательству.
Если в том же малом прямоугольном треугольнике обратить внимание на известный острый угол, то можно вывести значение высоты через синус угла в 60 градусов.
Синус – это отношение противолежащего катета к гипотенузе.
Воспользуемся этим отношением и выразим высоту.
$h=a*sin(60)=
Что мы узнали?
Мы узнали, что такое равносторонний треугольник, вывели несколько формул для нахождения высоты равностороннего треугольника. Показали несколько путей вывода формул, которые могут помочь быстро вспомнить, как находится высота или использовать те же приемы для нахождения других величин в равностороннем треугольнике.
Высота равностороннего треугольника
Какими свойствами обладает высота равностороннего треугольника? Как найти высоту равностороннего треугольника через его сторону, радиусы вписанной или описанной окружностей?
(свойство высоты равностороннего треугольника)
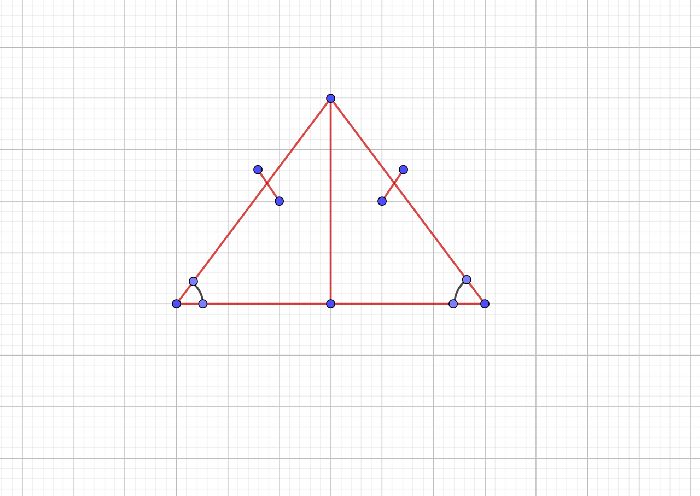
В равностороннем треугольнике высота, проведённая к любой стороне, является также его медианой и биссектрисой.
Доказательство :
Пусть в треугольнике ABC AB=BC=AC.
Так как AB=BC, треугольник ABC равнобедренный с основанием AC.
Проведём высоту BF.
По свойству равнобедренного треугольника, BF является также его медианой и биссектрисой
(то есть, AF=FC, ∠ABF=∠CBF).
Аналогично, рассмотрев треугольник ABC как равнобедренный с основанием BC и треугольник ABC — равнобедренный с основанием AB, доказываем, что высоты AK и CD являются также его медианами и биссектрисами
(то есть, BK=KC, ∠BAK=∠CAK; AD=BD, ∠ACD=∠BCD).
(свойство высот равностороннего треугольника)
Все три высоты равностороннего треугольника равны между собой.
Пусть в треугольнике ABC AB=BC=AC.
AK, BF и CD — его высоты.
В прямоугольных треугольниках ABF, BCD и CAK:
гипотенузы AB, BC и CA равны по условию,
∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника).
Следовательно, треугольники ABF, BCD и CAK равны (по гипотенузе и острому углу).
Из равенства треугольников следует равенство соответствующих сторон: BF=CD=AK.
Из теорем 1 и 2 следует, что в равностороннем треугольнике все высоты, медианы и биссектрисы равны между собой.
1) Найдём высоту равностороннего треугольника через его сторону.
В треугольнике ABC AB=BC=AC=a.
Рассмотрим прямоугольный треугольник ABF.
Отсюда формула высоты равностороннего треугольника через его сторону:
(2-й способ: из прямоугольного треугольника ABF по теореме Пифагора
2) Выразим высоту равностороннего треугольника через радиусы вписанной и описанной окружностей.
Точка O — центр правильного треугольника — является также центром его вписанной и описанной окружностей. Как центр вписанной окружности O — точка пересечения биссектрис треугольника. В правильном треугольнике биссектрисы и медианы совпадают. Следовательно, также является O точкой пересечения медиан.
А так как медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины, то BO:OF=2:1, то есть
BO — радиус описанной окружности, OF — вписанной: BO=R, OF=r.
Следовательно, высота равностороннего треугольника равна трём радиусам вписанной окружности:
и в полтора раза больше радиуса описанной окружности:
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Высота равностороннего треугольника
Свойства
Зная высоту в равностороннем треугольнике, вычислить сторону не составляет труда. Для этого нужно умножить высоту на два и разделить на корень из трех. a=2h/√3
Теперь имея равноценное стороне выражение, можно найти все остальные параметры равностороннего треугольника. Периметр равен утроенной стороне, в данном случае коэффициент сократится с корнем из трех, и периметр получится равен двум корням из трех, умноженным на высоту. P=3a=(3*2h)/√3=2√3 h
Чтобы найти площадь равностороннего треугольника через высоту, нужно корень из трех, деленный на четыре, умножить на выражение, соответствующее стороне, возведенное в квадрат. Получится высота в квадрате, деленная на корень из трех. S=√3/4 (2h/√3)^2=(√3 h^2)/3=h^2/√3
Медианы и биссектрисы через высоту в равностороннем треугольнике можно не считать, так как они равны между собой и совпадают при наложении. (рис.99) h=m=l
Средняя линия в равностороннем треугольнике расположена параллельно стороне таким образом, чтобы делить боковые стороны ровно пополам точками пересечения. При таком расположении средняя линия равна ровно половине стороны. Найти среднюю линию через высоту можно, разделив ее на корень из трех. (рис. 97.3) M=h/√3
Чтобы вычислить радиусы вписанной и описанной окружности около равностороннего треугольника, необходимо разделить сторону на два или один корень из трех соответственно. Таким образом, используя выражение стороны через высоту, корень из трех уходит и остаются следующие формулы. (рис. 97.4,97.5) r=a/(2√3)=h/3 R=a/√3=2h/3
Формулы, используемые для этого, несложны. Вывод выражений основан на свойствах треугольника, при этом точка пересечения высот считается замечательной и даже имеет своё название — ортоцентр.
Общие сведения
Три отрезка, не принадлежащие одной прямой, каждый из которых соединяется с другими в двух точках, образуют геометрическую фигуру — треугольник. Прямые линии — это стороны, а точки их соприкосновения вершины. Один из отрезков, обычно который проходит параллельно горизонтальной плоскости, называют основанием.
В зависимости от размера внутренних углов замкнутой фигуры, треугольники разделяют на следующие виды:
По числу равных сторон треугольные фигуры разделяют на разносторонние, равнобедренные, равносторонние. Последние часто называют правильными, так как все стороны у такого объекта равны друг другу. Кроме этого, из особенностей равносторонней фигуры можно отметить, что центры вписанной и описанной окружности совпадают, а каждый из углов равен 60 градусам. Сумма всех углов треугольника равняется 180 градусам.
В любой трёхугольной фигуре можно построить так называемые 3 замечательные линии: медиана, биссектриса и высота.
В правильном треугольнике эти 3 отрезка совпадают, то есть линия, опущенная из вершины к противолежащей стороне, одновременно являясь медианой, биссектрисой и высотой, образует прямой угол с основанием. При этом она делит его пополам. Фактически высота играет роль катета.
Получается, что в середине фигуры можно построить 3 отрезка, которые и будут высотами. Две из них будут опущены на боковые грани, а одна на основание. Точка пересечения перпендикулярных линий называется ортоцентром. Она располагается внутри геометрического тела и совпадает с центром вписанной окружности.
Для трёхугольного тела существует 2 теоремы. Одна из них утверждает, что противолежащие боковые стороны имеют одинаковую длину, а вторая, что если 2 угла невырожденного треугольника равны, то грани, противоположные им, также равны.
Интересно то, что эти правила справедливы как для абсолютной, так и сферической геометрии.
Свойства равносторонней фигуры
При решении задач, связанных с нахождением высоты в равностороннем треугольнике, часто приходится использовать его свойства. Зная их, найти нужные параметры будет несложно. Тем более что все они связаны с главной особенностью фигуры — равенством его всех сторон.
Равностороннее тело с тремя углами обладает следующими особенностями:
Эти свойства очевидны. Если начертить треугольник с равными сторонами и вписать его в окружность, за центр можно принять точку O, при этом радиус описанного круга будет OK. Тогда линия, проведённая из неё к вершине, будет радиусом. Пусть конечная точка будет B. Но так как место пересечения является общим и для высот и медиан, из свойства последних можно сделать вывод, что в точке линия делится в отношении 2 к 1. Отсчёт следует вести с вершины треугольника. Значит: OB = 2 * OK.
Из основных формул, которые используются при вычислениях, в первую очередь нужно запомнить:
Если рассмотреть треугольник ABC с проведённой высотой BN, можно утверждать, что грань АВ = ВС = АС = AN /2 = NC /2. Так как фигура ABN является копией BNC в зеркальном отражении, разделённые углы у вершины будут одинаковыми, а и их разворот составлять 30 градусов. Из этого следует, что угол A равен 60 градусам, значит, отрезок BN = AB * sin 60 0 = (AB * √3) / 2.
Зная длину медианы (высоты), вычислить другие параметры треугольника не составит труда. Например, периметр, P = 2 √3 * h; площадь — S = (h * 2) / √3.
При этом замечательным свойством является ещё и то, что ортоцентр одновременно будет в фигуре и центром тяжести (центроидом), поэтому точка пересечения высот и делит отрезок в отношении 2 к 1.
Формула высоты
В равностороннем треугольнике длина стороны равна произведению удвоенной высоты и квадратного корня из трёх. Эту формулу легко доказать, используя теорему Пифагора. Так как высота одновременно является и биссектрисой, она, проведённая на противоположное основание, разделяет треугольник на 2 симметричные фигуры. Исходя из того, что отрезок — это перпендикуляр, полученные геометрические тела будут прямоугольными.
Аналогичное определение можно получить, используя для доказательства формулу Герона. Отрезок, являющийся высотой, можно найти из выражения: h = (2 * √p * (p — a) * (p — b) * (p — a)) / b. В равенстве p является периметром и находится как сумма всех сторон: p = (a + b + a). Так как одна из граней делится пополам, формулу можно привести к виду: p = (a + b + a) / 2 = a + b / 2.
Для упрощения выражения под корень можно внести двойку и знаменатель b. Таким образом, формула примет вид: h = √(2 2 * (a 2 — (b/2) 2 * (b/2) 2 ) * b 2 ). Выполнив ряд сокращений, равенство можно будет представить: h = √(a 2 — (b 2 /4)). Из-за того, что стороны в трёхугольной фигуре совпадают, окончательный вариант можно записать: h = (a√3) / 2. Что и следовало доказать.
Высоту можно определить, и зная радиус вписанной окружности. Её можно найти по формуле: r = (a √ 3) / 6. Если выражение переписать как r = (1 / 3) * ((a √3) / 2), возможно увидеть, что второй множитель как раз и есть высота. Соответственно, r = (1/3) * h. Отсюда: h = 3 * r. Это довольно простая формула, которая часто используется при геометрических вычислениях, поэтому её тоже нужно запомнить.
Решение примеров
Самостоятельное решение задач позволяет закрепить теоретические знания и запомнить формулы. Существуют определённые типы примеров, с помощью которых можно довольно быстро проработать весь изученный материал. Вот некоторые из них, рассчитанные на учеников восьмых классов средней школы:
Проверить правильность решения можно, используя онлайн-калькуляторы. Это интернет-сервисы, которые позволяют своим пользователям в автоматическом режиме вычислять различные математические примеры. Свои услуги они предоставляют бесплатно, от пользователя требуется только установленный веб-обозреватель и подключение к сети.
Важно ещё, что калькуляторы не только выдают быстро правильный ответ, но и показывают пошаговое решение. Это очень удобно, когда необходимо определить, на каком этапе была допущена ошибка.
Кроме этого, на своих страницах такого рода сервисы содержат краткий теоретический материал и даже примеры заданий. Так что калькуляторы будут полезны и на стадии обучения.