В чем выражается жесткость пружины
Определение жесткости пружины
Жесткость — способность твёрдого тела, конструкции или её элементов сопротивляться деформации от приложенного усилия вдоль выбранного направления в заданной системе координат.
Сила жесткости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
От чего зависит жесткость
Жесткость пружины зависит от нескольких параметров:
Геометрия пружины
На жесткость витой пружины влияет:
Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.
Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.
Их основные геометрические параметры:
Тип материала
У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.
Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.
Предел упругости измеряют в паскалях и определяют по формуле:
где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.
Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие. Все они взаимосвязаны, поэтому, выяснив значение одной из величин с помощью справочной таблицы, можно вычислить другие.
Коэффициент
Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.
Эта линейная зависимость описывается формулой:
где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.
Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.
Срок эксплуатации
Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.
Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство. В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.
В чем измеряется жесткость
Жесткость пружины в системе СИ измеряется в ньютонах на метр, Н/м. Также встречается единица измерения ньютон на миллиметр, Н/мм. Численно жесткость равна величине силы, изменяющей размер пружины на метр длины.
Как обозначается
Коэффициент жесткости пружины обозначают буквой k.
Коэффициент жесткости пружины
Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.
Применяется в механике твердого тела в разделе упругости.
Формула расчета через массу и длину
Используя закон Гука, коэффициент жесткости можно вычислить по формуле:
Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:
где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.
Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.
При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:
Как можно измерить жесткость
Измерительные приборы
Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.
Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.
Практическая задача
Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.
Для измерения осевой жесткости спиральной пружины используют:
Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.
Альтернативные способы определения жесткости
Жесткость пружины можно определить и через период ее колебания, воспользовавшись формулой:
Или через частоту колебаний по формуле:
Проводя опыт с пружиной, закрепленной на штативе, и грузиками с известной массой, можно не измерять длину пружины, а привести ее в колебательное движение и сосчитать количество колебаний в период времени.
Формула расчета через длину, дающая более точные результаты и применимая к пружинам со значительной деформацией, различается для пружин разных геометрических параметров. Например, жесткость витой цилиндрической пружины, упруго деформируемой вдоль оси, вычисляется по формуле:
где \(d_D\) — диаметр проволоки, \(d_F\) — диаметр намотки, \(G\) — модуль сдвига, который зависит от материала, а \(n\) — число витков.
Задача
Рассчитайте коэффициент жесткости пружины, если известно, что ее диаметр 20 мм, диаметр проволоки 1 мм, число витков — 25. Модуль сдвига равен \(8\times\;10^<10>\;\) Па.
Решение
Переведем числовые значения в систему СИ и подставим в формулу:
Жесткость при деформации кручения существенно отличается от жесткости сжатия-растяжения. Предел прочности при кручении у любого материала будет меньше, чем предел прочности при сжатии-растяжении или изгибе. Торсионная жесткость, также называемая крутильной, в системе СИ измеряется в ньютон-метрах на радиан, сокращенно Н-м/рад. Ее можно определить по формуле:
где \(М\) — крутящий момент, приложенный к телу, а \(\alpha\) — угол закручивания тела по оси приложения крутящего момента.
Формула жесткости пружины
Определение и формула жесткости пружины
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
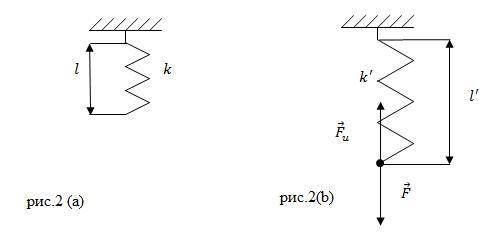
Рассмотрим пружину, на которую действует растягивающая сила ($\overline
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
При последовательном соединении пружин жесткость системы определяют как:
Примеры задач с решением
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
При упругих деформациях выполняется закон Гука:
\[F=k\Delta l\ \left(1.2\right).\]
Из (1.2) найдем удлинение пружины:
Длина растянутой пружины равна:
Вычислим новую длину пружины:
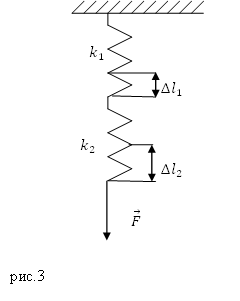
Решение. Если пружины соединены последовательно, то деформирующая сила ($\overline
Для второй пружины запишем:
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
\[k_1\Delta l_1=k_2\Delta l_2\left(2.3\right).\]
Из равенства (2.3) получим удлинение первой пружины:
Как найти коэффициент жёсткости пружины: формула, определение
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
В свою очередь, упругими деформациями будут считаться:
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
Последовательность действий для опыта такова:
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Жесткость пружины
При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
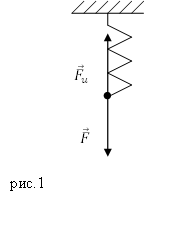
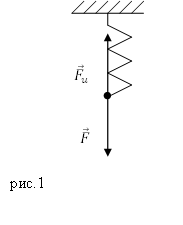
Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.
При воздействии деформирующей силы ($\overline
Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:
Единицы измерения жесткости пружины
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Жесткость соединений пружин
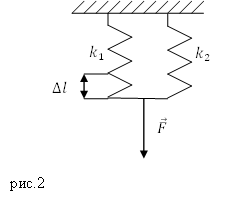
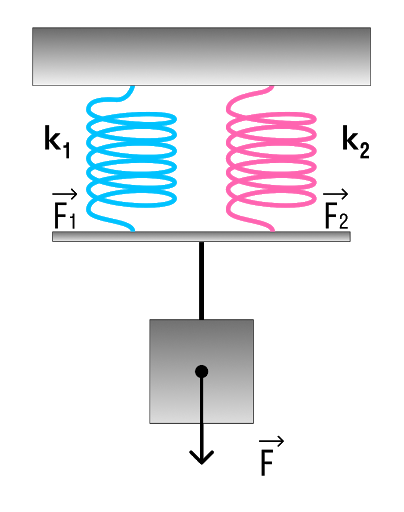
Если пружины соединены параллельно, то результирующая жесткость равна:
Примеры задач на жесткость пружин
Решение. При параллельном соединении пружин жесткость системы вычислим как:
Потенциальную энергию деформированной системы вычислим при помощи формулы:
Вычислим искомую потенциальную энергию:
Решение. Сделаем рисунок.
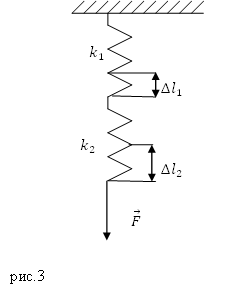
При последовательном соединении пружин на каждую из них действует одна и та же деформирующая сила ($\overline
\[F=k_1\Delta l_1=k_2\Delta l_2\to \Delta l_1=\frac
Работа силы упругости при растяжении первой пружины, равна:
Учитывая полученное в (2.1) удлинение первой пружины имеем:
Работа второй силы упругости:
Работа силы, которая растягивает систему пружин в целом, будет найдена как:
Подставим правые части выражений (2.3) и (2.4) в формулу (2.5), получаем:
Сила упругости
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
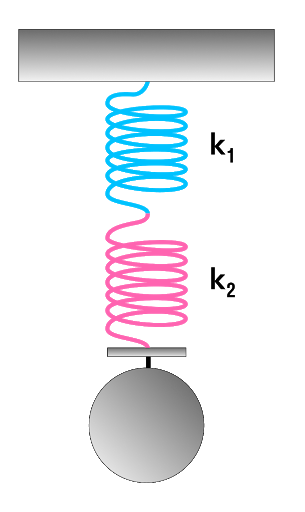
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
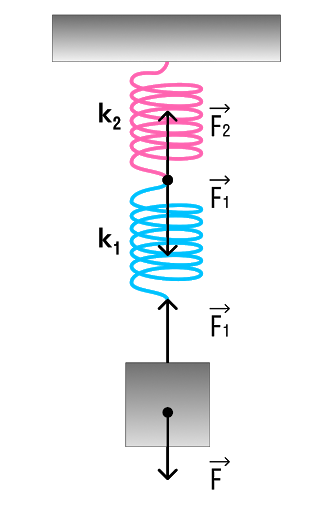
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
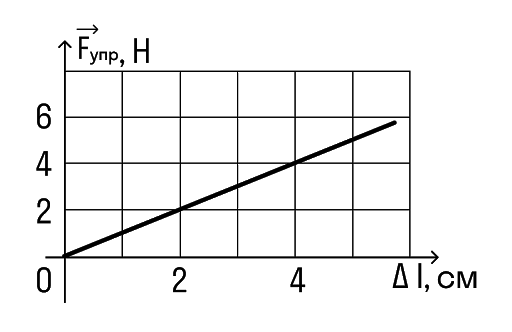
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
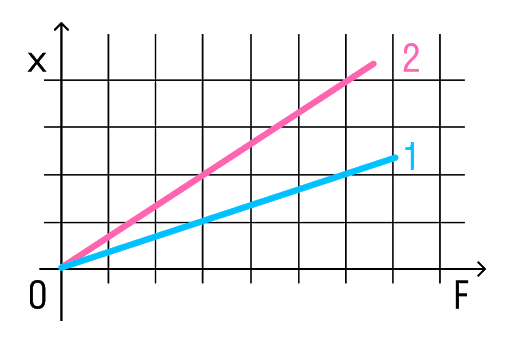
Задачка 2
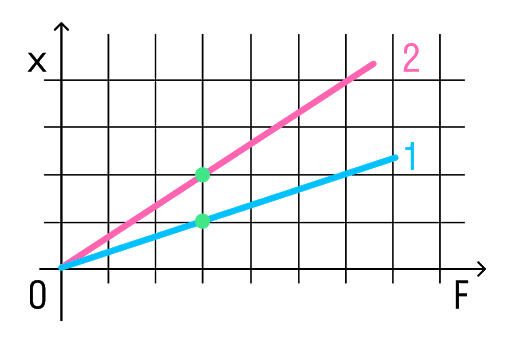
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.