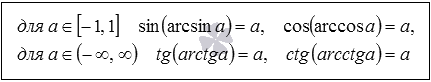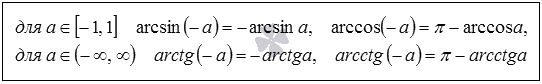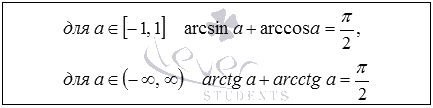Арксинус синуса чему равен
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.
В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.
Навигация по странице.
Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.
Синус арксинуса, косинус арккосинуса и т.п.
Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Арксинус синуса, арккосинус косинуса и т.п.
Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.
Связи между arcsin, arccos, arctg и arcctg противоположных чисел
Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.
Синус от арккосинуса, тангенс от арксинуса и иже с ними
На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.
Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид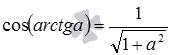 
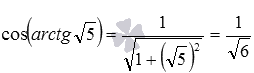
, таким образом 
.
Другой пример: используя формулу синуса арккосинуса вида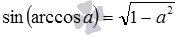 
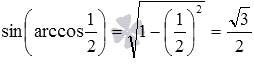
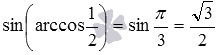
, мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем 
. Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: 
(при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).
Осталось показать вывод записанных формул.
Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.
Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств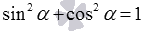 
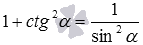
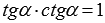
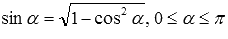
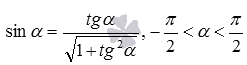
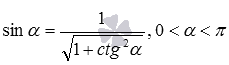
и 
, а также учитывая, что 
, легко получить следующие формулы 
, 
и 
, выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.
Вот краткая запись вышеперечисленных выкладок:
По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:
Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:
Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как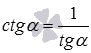 
.
arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.
По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:
Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:
Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:
Наконец, вот ряд формул с арккотангенсом:
Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.
Для примера, докажем, что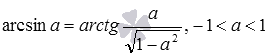 
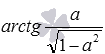
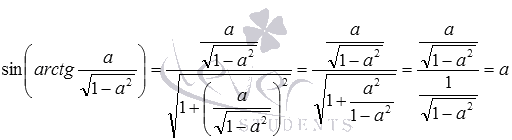
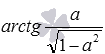
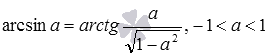
. Известно, что 
при указанных a представляет собой угол (число) от минус пи пополам до пи пополам. Более того, по формуле синуса арктангенса имеем 
. Следовательно, при −1 является арксинусом числа a по определению, то есть, .
По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.
В данном примере мы могли вычислить требуемое значение и непосредственно: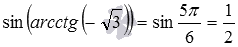 
. Очевидно, что мы получили тот же результат.
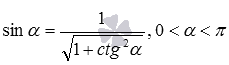
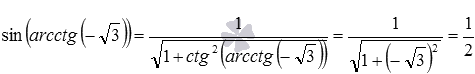
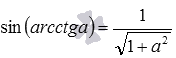
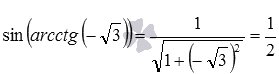
Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида . Тогда решение выглядело бы так: 
. А можно было и сразу применить формулу синуса арккотангенса вида 
: 
.
Некоторые другие формулы
Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
sin ( a r c sin a ) = a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
Пример 1. Свойства обратных тригонометрических функций
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccos
Соответственно, для арктангенса и арккотангенса
Сумма arctg и arcctg
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинуса
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Повторим определение еще раз:
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Значит, областью определения функции y = arcsin x является отрезок
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
Строим график функции
1. Область определения
2. Область значений
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Заполним таблицу, пользуясь определением арккосинуса.
Вот график арккосинуса:
1. Область определения
2. Область значений
Эта функция общего вида — она не является ни четной, ни нечетной.
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
1. Область определения
2. Область значений
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Арксинус. Решение простейших уравнений с синусом. Часть 2
Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac<π><2>;\frac<π><2>]\) синус которого равен \(a\) т.е.
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:
Как вычислить арксинус?
Например, вычислите значение арксинуса:
а) Синус какого числа равен \(-\frac<1><2>\)? Или в более точной формулировке можно спросить так: если \(\sin x=-\frac<1><2>\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac<π><2>\) и \(\frac<π><2>\). Ответ очевиден:
б) Синус какого числа равен \(\frac<\sqrt<3>><2>\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac<π><3>\).
Тригонометрический круг со всеми стандартными арксинусами:
Зачем нужен арксинус? Решение уравнения \(\sin x=a\)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin x=\frac<1><2>\).
Это не вызывает затруднений:
А теперь решите уравнение: \(\sin x=\frac<1><3>\).
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac<1><3>\), потому что известно, что синус равен \(\frac<1><3>\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin\frac<1><3>\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin\frac<1><3>\) от \(π\), то её значение составляет \(π- \arcsin\frac<1><3>\).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin
С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac<1><\sqrt<3>>\).
Решение:
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac<1><\sqrt<2>>\).
Значит в ответе вместо арксинусов нужно написать \(\frac<π><4>\).
Пример. Решите тригонометрическое уравнение: \(\sin x=\frac<7><6>\).
Решение:
И вновь тот, кто поторопился написать \( \left[ \begin
Думаю, вы уловили закономерность.
Если \(\sin x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \beginx= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end\right.\)
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:
Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin(-\frac<\sqrt<7>><2>)\) в принципе неверна, ведь \(-\frac<\sqrt<7>> <2>Синус
Тригонометрические уравнения
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
Теперь разберем примеры, как они применяются в задачах.
Решение
У нас для этого есть подходящая формула следующего вида: cos ( a r c t g α ) = 1 1 + α 2
Подставляем нужное значение: cos ( a r c t g 5 ) = 1 1 + ( 5 ) 2 = 2 6
Решение
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin ( a r c cos 1 2 ) = sin π 3 = 3 2
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
sin 2 α + cos 2 α = 1 1 + c t g 2 α = 1 sin 2 α
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
Следовательно, sin ( a r c t g α ) = t g ( a r c t g α ) 1 + t g 2 ( a r c t g α ) = α 1 + α 2
Следовательно, sin ( a r c t g α ) = 1 1 + t g 2 ( a r c t g α ) = 1 1 + α 2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
следует, что cos ( a r c t g α ) = c t g ( a r c c t g α ) 1 + c t g 2 ( a r c c t g α ) = α 1 + α 2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
А так мы выразим арккосинус через остальные обратные функции:
Формула выражения арктангенса:
Последняя часть – выражение арккотангенса через другие обратные функции:
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Решение
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.