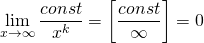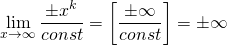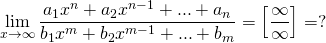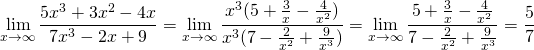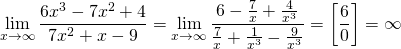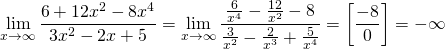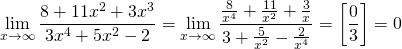если бесконечность разделить на бесконечность что будет
Если бесконечность разделить на бесконечность что будет
http://uzdikbalabaksha.kz/index.php/competitions/9-zdik-sport-jirmesi
Здравствуйте! Проголосуйте пожалуйста за детский садик Акбота в городе Акколь! Спасибо огромное .
Так как это полные абстракции («бесконечно большие величины»), то с ними можно производить стандартные математические действия.
Понял
,В МАРТЕ МОЖЕТ СМОГУ НОВЫЙ КУПИТЬ.
Интересно вы рассуждаете. Ну допустим, что профессора не люди, которые никогда не смеются и полностью потеряны. Поэтому вот такой у меня вопрос: А что значит потеряно (или не потеряно) и для кого?
не уверен, что я прав, но по моему любое действия связанное с бесконечностью порождает бесконечность.
Не, бесконечности бывают разные)
Величины могут стремиться к бесконечности с экспоненциальной скоростью, могут с линейной, полиномиальнй и тд. Если взять отношение 2х экспоненциальных величин, или двух линейных и устремить их к бесконечности, то в первом случае может получиться или бесконечнось или константа, а во втором только константа.
но, подождите, здесь берутся величины, которые стремятся к бесконечности, с разной скоростью, или с разной прогрессии в скорости, стремящиеся к бесконечности. Величины ведь только стремятся, но сами не являются бесконечностью. Хотя они могут породить бесконечность, как достигшая величина n в n бесконечной степени.
В пределе они стремятся к бесконечности.
Можно. Но это неопределенность. Дохрена разделить на дофига не имеет отпределенного решения )
Делить возможно нет, а вот прибавлять. Галактики неосязаемы, но их много во вселенной.
тебе оно надо? Тут судьбы людей решаются, а ты со своими бесконечностями)))
Основные неопределенности пределов и их раскрытие
В предыдущей статье мы рассказывали, как правильно вычислять пределы элементарных функций. Если же мы возьмем более сложные функции, то у нас в расчетах появятся выражения с неопределенным значением. Они и называются неопределенностями.
Выделяют следующие основные виды неопределенностей:
Мы перечислили все основные неопределенности. Другие выражения в различных условиях могут принимать конечные или бесконечные значения, следовательно, они не могут считаться неопределенностями.
Раскрытие неопределенностей
Раскрыть неопределенность можно:
С помощью замечательных пределов;
С помощью правила Лопиталя;
Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
Всю информацию, представленную выше, можно наглядно представить в виде таблицы. С левой стороны в ней приводится вид неопределенности, с правой – подходящий метод ее раскрытия (нахождения предела). Этой таблицей очень удобно пользоваться при расчетах, связанных с нахождением пределов.
| Неопределенность | Метод раскрытия неопределенности |
| 1. Деление 0 на 0 | Преобразование и последующее упрощение выражения. Если выражение имеет вид sin ( k x ) k x или k x sin ( k x ) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений |
| 2. Деление бесконечности на бесконечность | Преобразование и упрощение выражения либо использование правила Лопиталя |
| 3. Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями | Преобразование в » open=» 0 0 или » open=» ∞ ∞ с последующим применением правила Лопиталя |
| 4. Единица в степени бесконечности | Использование второго замечательного предела |
| 5. Возведение нуля или бесконечности в нулевую степень | Логарифмирование выражения с применением равенства lim x → x 0 ln ( f ( x ) ) = ln lim x → x 0 f ( x ) |
Разберем пару задач. Эти примеры довольно простые: в них ответ получается сразу после подстановки значений и неопределенности при этом не возникает.
Решение
Выполняем подстановку значений и получаем ответ.
Решение
Значит, мы можем преобразовать предел в следующее выражение:
Далее мы приведем примеры решений задач на раскрытие неопределенностей с использованием метода преобразования. На практике выполнять это приходится довольно часто.
Решение
Выполняем подстановку значений.
В итоге у нас получилась неопределенность. Используем таблицу выше, чтобы выбрать метод решения. Там указано, что нужно выполнить упрощение выражения.
Как мы видим, упрощение привело к раскрытию неопределенности.
Решение
Подставляем значение и получаем запись следующего вида.
Домножение знаменателя выполняется для того, чтобы потом можно было воспользоваться формулой сокращенного умножения (разность квадратов) и выполнить сокращение.
Как мы видим, в результате этих действий нам удалось избавиться от неопределенности.
Важно отметить, что при решении подобных задач подход с использованием домножения используется очень часто, так что советуем запомнить, как именно это делается.
Решение
Выполняем разложение числителя на множители:
Теперь делаем то же самое со знаменателем:
Мы получили предел следующего вида:
Как мы видим, в ходе преобразования нам удалось избавиться от неопределенности.
Решение
Решение
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = » open=» ∞ ∞
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = » open=» ∞ ∞ = lim x → ∞ x 8 + 11 3 x 8 3 x 2 + x + 1 x 8 3 = = lim x → ∞ 1 + 11 x 8 3 1 x 2 3 + 1 x 5 3 + 1 x 8 3 = 1 + 11 ∞ 3 1 ∞ + 1 ∞ + 1 ∞ = 1 + 0 3 0 + 0 + 0 = 1 0 = ∞
Решение
Выводы
В случае с пределом отношений возможны три основных варианта:
Если степень числителя равна степени знаменателя, то предел будет равен отношению коэффициентов при старших степенях.
Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.
Если степень числителя меньше степени знаменателя, то предел будет равен нулю.
Другие методы раскрытия неопределенностей мы разберем в отдельных статьях.
Пределы на бесконечность на бесконечность. Примеры.
Рассмотрим пределы на раскрытие неопределенности вида бесконечность на бесконечность.
Сначала учтем следующее:
— если при вычислении предела в числителе дроби стоит число, то
— это предел на неопределенность вида бесконечность, деленная на бесконечность (или просто бесконечность на бесконечность).
Чтобы найти предел, надо раскрыть неопределенность вида бесконечность на бесконечность. Для этого и в числителе, и в знаменателе выносим за скобки степень с наибольшим показателем. Затем сокращаем на нее.
В дальнейшем просто делим почленно числитель и знаменатель (то есть каждое слагаемое) на старшую степень икса.
2)
А теперь сделаем выводы. Пределы на неопределенность бесконечность на бесконечность сводятся к одному из трех вариантов: