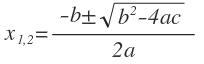если дискриминант отрицательный в неравенстве что делать

Квадратные неравенства

Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.

В зависимости от значения a ветви графика направлены вверх или вниз:

Квадратные неравенства имеют вид.

ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0

Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?

Как решать квадратные неравенства?

Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).

Пример:

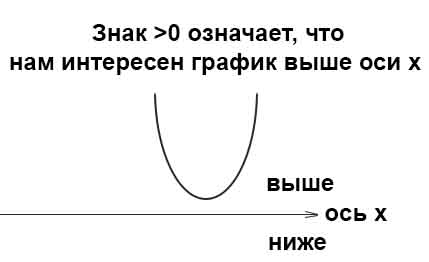
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)

Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.

Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.

Пример:

Рассмотрим этот же пример со знаком неравенства меньше 0

Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.

А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0

Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.

Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0

Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.

Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Также можно решить методом интервалов. Ось x делится на три участка.

Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.

Второй участок (-2; 1). На этом участке можно взять число 0.

Третий участок (1; +∞). На этом участке возьмем число 2.

Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.

Источник

Как найти дискриминант квадратного уравнения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие квадратного уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.

Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.

Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Чаще всего для поиска дискриминанта используют формулу:

В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:

Эта формула подходит даже для неполных квадратных уравнений.

Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.

Как решать квадратные уравнения через дискриминант

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!

Примеры решения квадратных уравнений с помощью дискриминанта

Ответ: корень уравнения 3.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Источник

Метод интервалов, решение неравенств

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение квадратного неравенства

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

Квадратное неравенство можно решить двумя способами:

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Неравенство примет вид:

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Неравенства. Квадратные неравенства.

Квадратными неравенствами обозначают неравенства типа

В результате можем иметь нижеследующие варианты:

1) При D = 0 у квадратного уравнения один корень:

.

2) При D>0 у квадратного уравнения два корня. Парабола пересекает ось х в двух точках с абсциссами:

Если необходимо указать отрезок, на котором квадратный трехчлен положителен, то это отрезок расположен там, где парабола расположена над осью x. По аналогии если необходимо найти отрицательные значения, то берем отрезок, где парабола расположена под осью x

При решении неравенства ax 2 +bx +c > 0 не требуется тщательно строить параболу у= ax 2 +bx +c по точкам (к примеру, вовсе нет необходимости вычислять вершину параболы, точку пересечения с осью у и т. д.). Допустимо упрощенно изобразить кривую. Точность необходима только при вычислении корней уравнения ax 2 +bx +c=0 (при D > 0).

Источник

Дискриминант

Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.

Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt\) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед \(\sqrt\)

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Источник

• ← если дисбактериоз кишечника что делать
• если дицинон не останавливает кровотечение что делать →