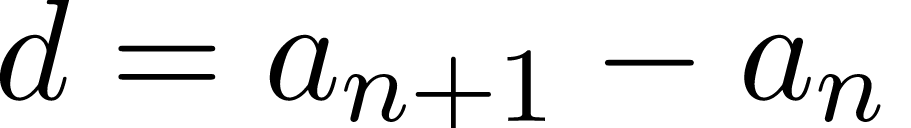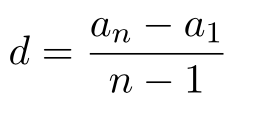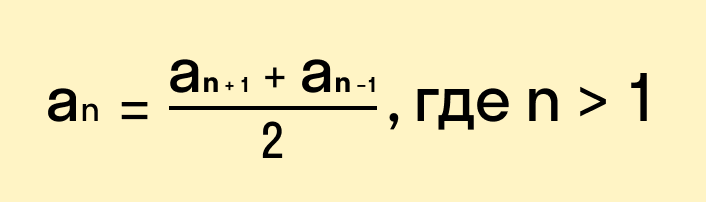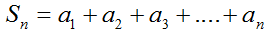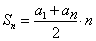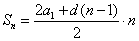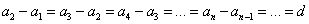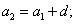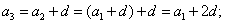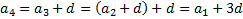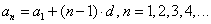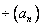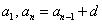как доказать что последовательность является арифметической прогрессией
Арифметическая прогрессия. Часть 1



Последовательность можно задать тремя способами:
Например, Некто решил заняться личным тайм-менеджментом, и для начала посчитать в течение недели, сколько времени он проводит ВКонтакте. Записывая время в таблицу, он получит последовательность, состоящую из семи элементов:
2. Последовательность можно задать с помощью формулы n-го члена.
В этом случае зависимость значения элемента последовательности от его номера выражается напрямую в виде формулы.
Например, если 
Чтобы найти значение элемента последовательности с заданным номером, мы номер элемента подставляем в формулу n-го члена.
То же самое мы делаем, если нужно найти значение функции, если известно значение аргумента. Мы значение аргумента подставляем вместо 
Если, например, 
Ещё раз замечу, что в последовательности, в отличие от произвольной числовой функции, аргументом может быть только натуральное число.
Например, рассмотрим последовательность 
Мы можем находить значения членов последовательности один за другим, начиная с третьего:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Число 
Если 

Например, 2; 5; 8; 11;.
Если 
Если 
Основное свойство арифметической прогрессии:
Посмотрим на рисунок.

Сложив эти два равенства, получим:

Разделим обе части равенства на 2:
Итак, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
Больше того, так как






Формула 
Мы видим, что для членов арифметической прогрессии выполняются соотношения:
и, наконец,
Мы получили формулу n-го члена.
ВАЖНО! Любой член арифметической прогрессии можно выразить через 

Сумма n членов арифметической прогрессии.
В произвольной арифметический прогрессии суммы членов, равноотстоящих от крайних равны между собой:
Рассмотрим арифметическую прогрессию, в которой n членов. Пусть сумма n членов этой прогрессии равна 
Расположим члены прогрессии сначала в порядке возрастания номеров, а затем в порядке убывания:
Сложим попарно:
Сумма в каждой скобке равна 
Итак, сумму n членов арифметической прогрессии можно найти по формулам:
Рассмотрим решение задач на арифметическую прогрессию.
Докажем, что разность между двумя соседними членами последовательности равна одному и тому же числу.
Мы получили, что разность двух соседних членов последовательности не зависит от их номера и является константой. Следовательно, по определению, эта последовательность является арифметической прогрессией.
а) Найдите 31 член прогрессии.
б) Определите, входит ли в данную прогрессию число 41.
а) Мы видим, что 
Запишем формулу n-го члена для нашей прогрессии.
В общем случае
В нашем случае 
б) Предположим, что число 41 является членом последовательности. Найдем его номер. Для этого решим уравнение:
Мы получили натуральное значение n, следовательно, да, число 41 является членом прогрессии. Если бы найденное значение n не было бы натуральным числом, то мы бы ответили, что число 41 НЕ является членом прогрессии.
б) Найдите сумму членов полученной прогрессии.
а) Вставим между числами 2 и 8 четыре числа:
Мы получили арифметическую прогрессию, в которой 6 членов.
Найдем разность этой прогрессии. Для этого воспользуемся формулой n-го члена:
Теперь легко найти значения чисел:
б)
Ответ: а) да; б) 30
4. Грузовик перевозит партию щебня массой 240 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено на двенадцатый день, если вся работа была выполнена за 15 дней.
По условию задачи количество щебня, которое перевозит грузовик, каждый день увеличивается на одно и то же число. Следовательно, мы имеем дело с арифметической прогрессией.
Сформулируем эту задачу в терминах арифметической прогрессии.
За первый день было перевезено 2 тонны щебня: [pmath size=14]a_1=2[/pmath].
Вся работа была выполнена за 15 дней: 
Грузовик перевозит партию щебня массой 240 тонн:
Нам нужно найти 
Сначала найдем разность прогрессии. Воспользуемся формулой суммы n членов прогрессии.
Найдем 
Ответ: 24.
Арифметическая прогрессия свойства и формулы
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
«Последовательность простых чисел: 4, 6, 10, 19, 21, 33. »
Последовательность yn = C называют постоянной или стационарной.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
Возрастающие и убывающие последовательности называют монотонными последовательностями.
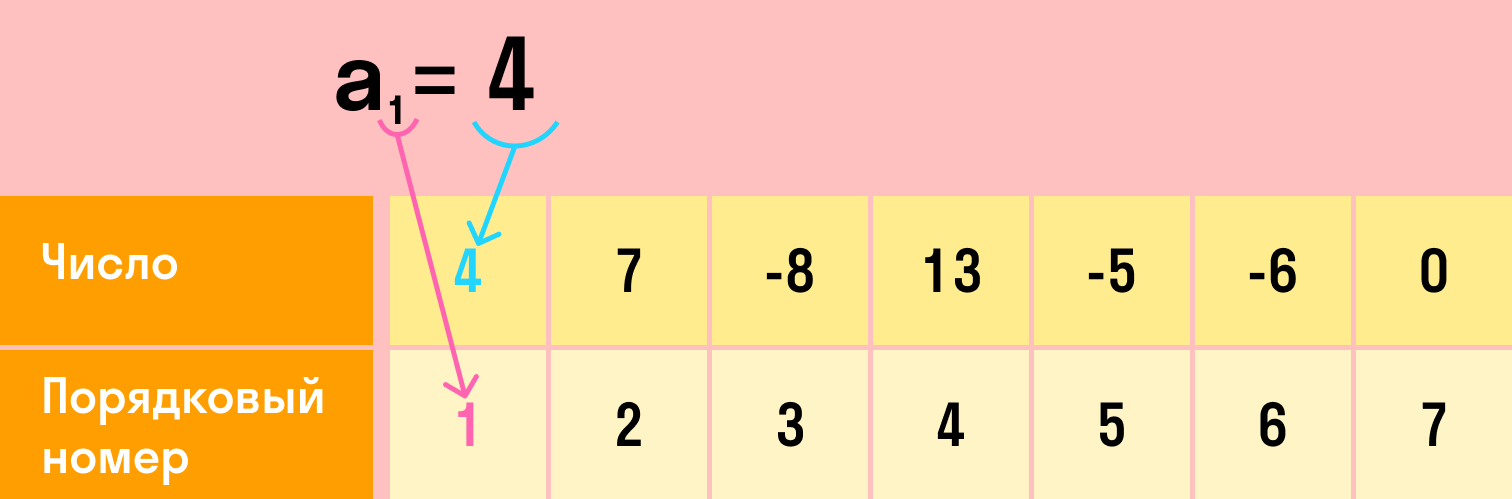
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2. a10. an.
N-ый член последовательности можно задать формулой. Например:
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.