как определить что число целое
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
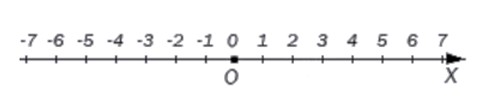
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
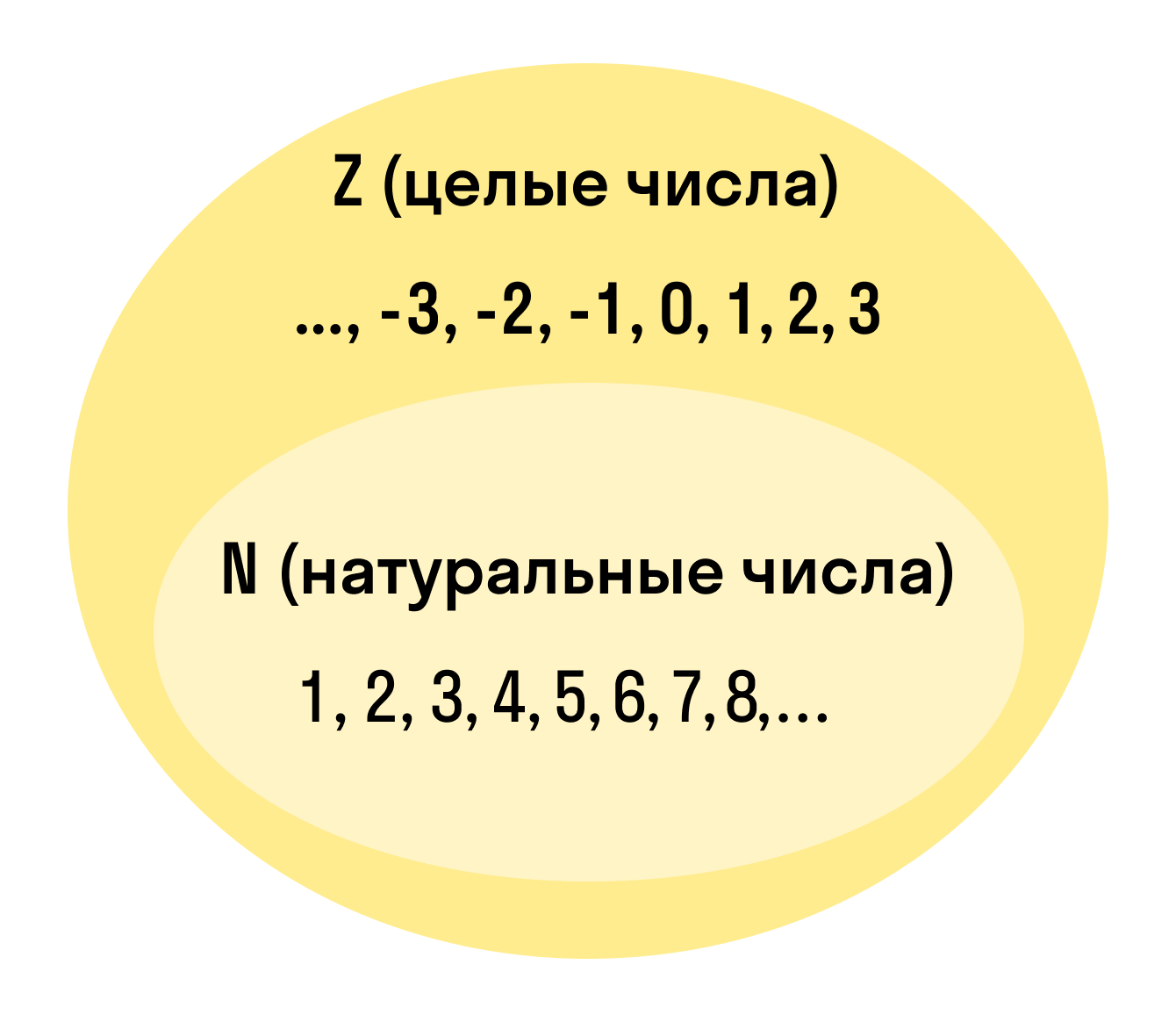
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Числа. Целые числа. Свойства целых чисел.
Целые числа – это натуральные числа, а также противоположные им числа и нуль.
Целые числа — расширение множества натуральных чисел N, которое получается путем добавления к N 0 и отрицательных чисел типа − n. Множество целых чисел обозначают Z.
Сумма, разность и произведение целых чисел дают снова целые числа, т.е. целые числа составляют кольцо относительно операций сложения и умножения.
Целые числа на числовой оси:
Сколько целых чисел? Какое количество целых чисел? Самого большого и самого маленького целого числа нет. Этот ряд бесконечен. Наибольшее и наименьшее целое число не существует.
Натуральные числа еще называются положительными целыми числами, т.е. фраза «натуральное число» и «положительное целое число» это одно и то же.
Ни обыкновенные, ни десятичные дроби не являются целыми числами. Но существуют дроби с целыми числами.
Операции над целыми числами.
1. Сумма целых чисел.
Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.
2. Вычитание целых чисел.
Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.
3. Умножение целых чисел.
Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.
Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.
(–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).
4. Деление целых чисел.
Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.
Свойства целых чисел.
Z не замкнуто относительно деления 2-х целых чисел (например, 1/2). Ниже приведенная таблица показывает некоторые основные свойства сложения и умножения для любых целых a, b и c.
Целые числа. Определение.
Существуют множество разновидностей чисел, одни из них – это целые числа. Целые числа появились для того, чтобы облегчить счет не только в положительную сторону, но и в отрицательную.
Ряд целых чисел.
Этот ряд чисел называется рядом целых чисел.
Целые положительные числа. Целые отрицательные числа.
Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля идут натуральные числа или их еще называют целыми положительными числами. А слева от нуля идут целые отрицательные числа.
Нуль не является ни положительным ни отрицательным числом. Он является границей между положительными и отрицательными числами.
Целые числа – это множество чисел, состоящие из натуральных чисел, целых отрицательных чисел и нуля.
Ряд целых чисел в положительную и в отрицательную сторону является бесконечным множеством.
Если мы возьмём два любых целых числа, то числа, стоящие между этими целыми числами, будут называться конечным множеством.
Натуральные числа обозначаются латинской буквой N.
Целые числа обозначаются латинской буквой Z. Все множество натуральных чисел и целых чисел можно изобразить на рисунке. 
Неположительные целые числа другими словами – это отрицательные целые числа.
Неотрицательные целые числа – это положительные целые числа.
Вопросы по теме:
Как называются числа, находящиеся в ряду целых чисел: а) справа от нуля; б) слева от нуля?
Ответ: а) натуральные числа или целые положительные числа. Оба термина несут один и тот же смысл.
б) целые отрицательные числа.
Назовите наибольшее целое число?
Ответ: ряд положительных целых чисел бесконечен, поэтому наибольшего целого числа не существует.
Какое наименьшее целое число?
Ответ: ряд отрицательных чисел бесконечен, поэтому наименьшего целого числа не существует.
Числа. Целые числа. Свойства целых чисел.
Целые числа – это натуральные числа, а также противоположные им числа и нуль.
Целые числа — расширение множества натуральных чисел N, которое получается путем добавления к N 0 и отрицательных чисел типа − n. Множество целых чисел обозначают Z.
Сумма, разность и произведение целых чисел дают снова целые числа, т.е. целые числа составляют кольцо относительно операций сложения и умножения.
Целые числа на числовой оси:
Сколько целых чисел? Какое количество целых чисел? Самого большого и самого маленького целого числа нет. Этот ряд бесконечен. Наибольшее и наименьшее целое число не существует.
Натуральные числа еще называются положительными целыми числами, т.е. фраза «натуральное число» и «положительное целое число» это одно и то же.
Ни обыкновенные, ни десятичные дроби не являются целыми числами. Но существуют дроби с целыми числами.
Операции над целыми числами.
1. Сумма целых чисел.
Для сложения двух целых чисел с одинаковыми знаками, необходимо сложить модули этих чисел и перед суммой поставить итоговый знак.
2. Вычитание целых чисел.
Для сложения двух целых чисел с разными знаками, необходимо из модуля числа, которое больше вычесть модуль числа, которое меньше и перед ответом поставить знак большего числа по модулю.
3. Умножение целых чисел.
Для умножения двух целых чисел, необходимо перемножить модули этих чисел и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.
Когда умножаются несколько чисел, знак произведения будет положительным, если число неположительных сомножителей чётное, и отрицателен, если нечётное.
(–2) ∙ (+3) ∙ (–5) ∙ (–3) ∙ (+4) = –360 (3 неположительных сомножителя).
4. Деление целых чисел.
Для деления целых чисел, необходимо поделить модуль одного на модуль другого и поставить перед результатом знак «+», если знаки чисел одинаковые, и минус, – если разные.
Свойства целых чисел.
Z не замкнуто относительно деления 2-х целых чисел (например, 1/2). Ниже приведенная таблица показывает некоторые основные свойства сложения и умножения для любых целых a, b и c.