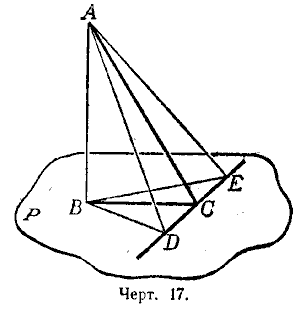
как определить что прямая наклонная к плоскости
Ортогональнальная проекция прямой на плоскость.
Угол между прямой и плоскостью.
Теорема о трех перпендикулярах
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
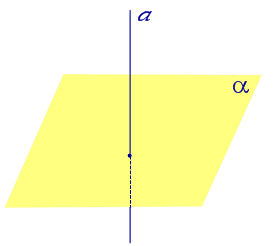
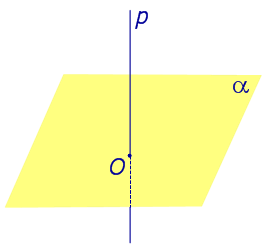
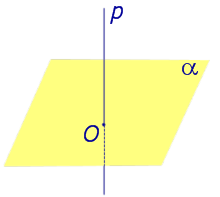
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
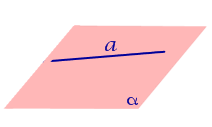
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
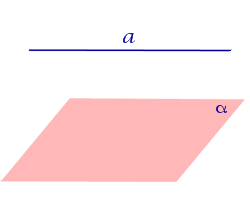
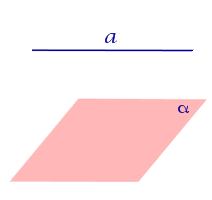
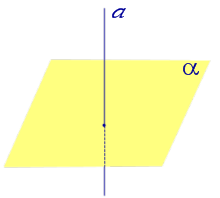
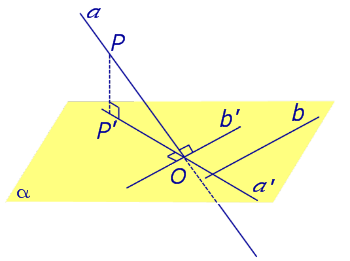
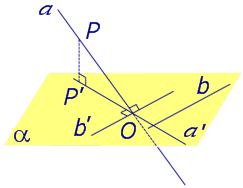
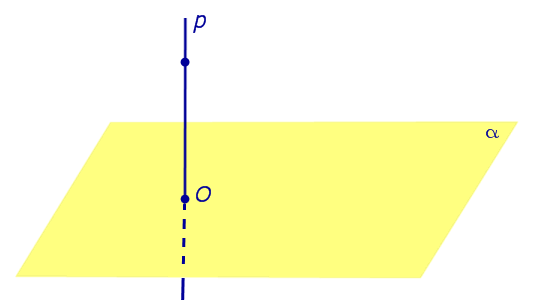
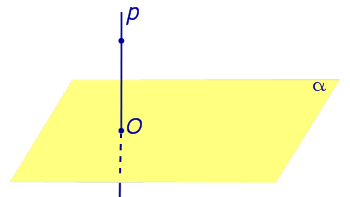
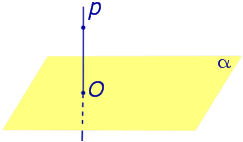
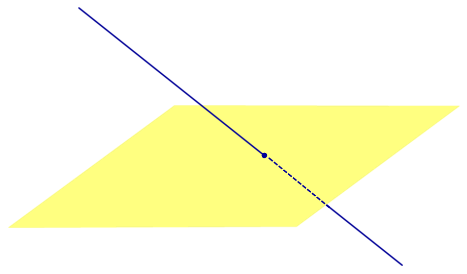
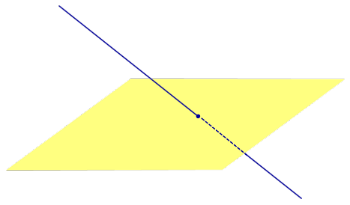
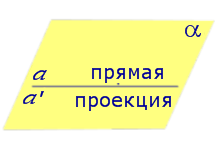
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
| Фигура | Рисунок | Свойство проекции | |||||||||||||||||||||||||
| Наклонная к плоскости α | 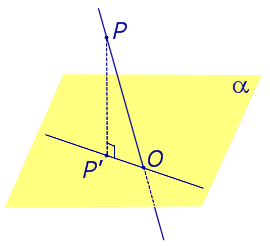 |
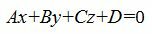 | (1) |
где n(A,B,C)− называется нормальным вектором плоскости.
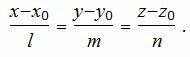 | (2) |
 | (3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
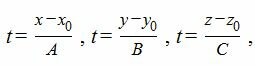 |
Выразим переменные x, y, z через рараметр t.
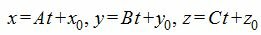 | (4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
| A(At+x )+B(Bt+y )+C(At+z )+D=0, |
| A 2 t+Ax +B 2 t+By +C 2 t+Cz +D=0, |
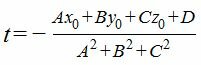 | (5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M на плоскость (1).
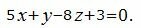 | (6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M и нормального вектора плоскости в (5), получим:
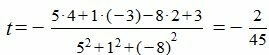 | (7) |
Из выражений (7) находим:
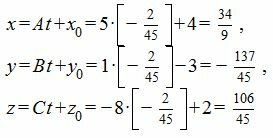 |
 Проекция точки на плоскость. Проекция прямой на плоскость Проекция точки на плоскость. Проекция прямой на плоскость |
 Угол между прямой и плоскостью Угол между прямой и плоскостью |
 Теорема о трех перпендикулярах. Обратная теорема Теорема о трех перпендикулярах. Обратная теорема |
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
| Фигура | Рисунок | Свойство проекции |
| Наклонная к плоскости α |  |
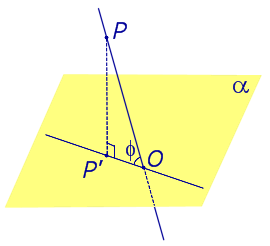
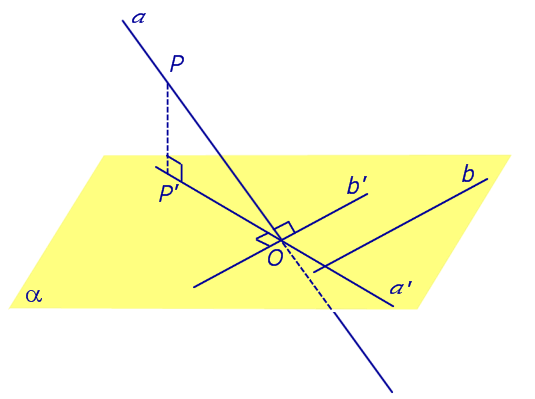
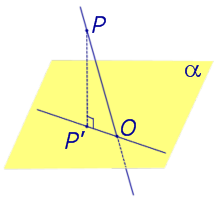
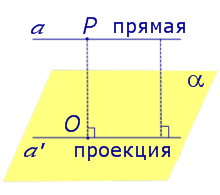
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
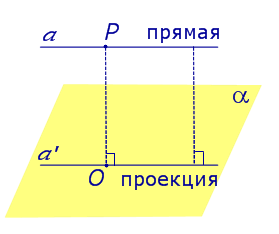
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
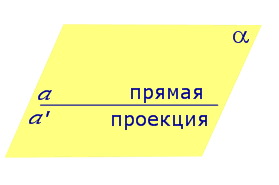
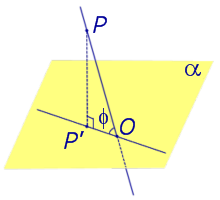
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.

 радиан).
радиан).