как определить что треугольник равносторонний
Признаки равенства треугольников
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Общие сведения
Любое пространство можно описать размерностью. В трёхмерном измерении плоская геометрическая фигура, состоящая из трёх отрезков и такого же количества точек, в которых они соединяются, называется треугольником. Отрезки называют сторонами или боковыми гранями, площадь, ограниченная ими — внутренней, а точки — вершинами. Фигура имеет 3 угла и является невырожденной.
Строгого требования к обозначениям элементов многоугольника нет. Но традиционно вершины подписывают заглавными буквами латинского алфавита A, B, C, а противолежащие им стороны — аналогичными строчными знаками. В качестве обозначений для углов используют греческие символы: α, β, γ. Например, если имеется треугольник ABC, у него будут углы A, B, C и стороны a, b, c. Боковые грани могут подписываться и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA.
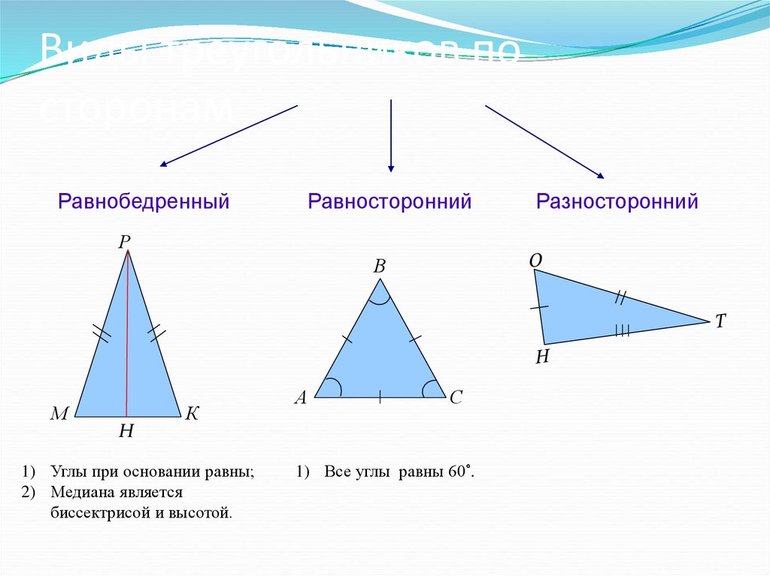
В зависимости от соотношения размеров сторон, все треугольники разделяют на 3 вида. Они бывают:
Существуют правила, позволяющие утверждать о равенстве или подобии двух и более треугольников. Они считаются идентичными, то есть их параметры полностью совпадают, если 2 стороны и угол равны или все грани имеют одинаковую длину. А также фигуры будут одинаковыми, когда у них совпадают 2 стороны и угол, располагающийся напротив большего отрезка.
Признаки подобия помогают определить вид треугольника при сравнении с известным. Если 2 любых угла равны в обеих фигурах, они считаются похожими. Когда же 2 стороны многоугольника пропорциональны двум отрезкам другого, причём углы, заключённые между этими гранями, равны, такие фигуры подобны.
Особые линии и точки
Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.
В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.
Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:
Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.
Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.
Точка, в которой пересекаются отрезки, будет центром тяжести фигуры. Её особенность в том, что она разделяет эту линию на 2 части в отношении 2 к 1, если считать от угла. Кроме этого, из-за равенства медианы и биссектрисы эта точка будет и ортоцентром.
Основные формулы
Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.
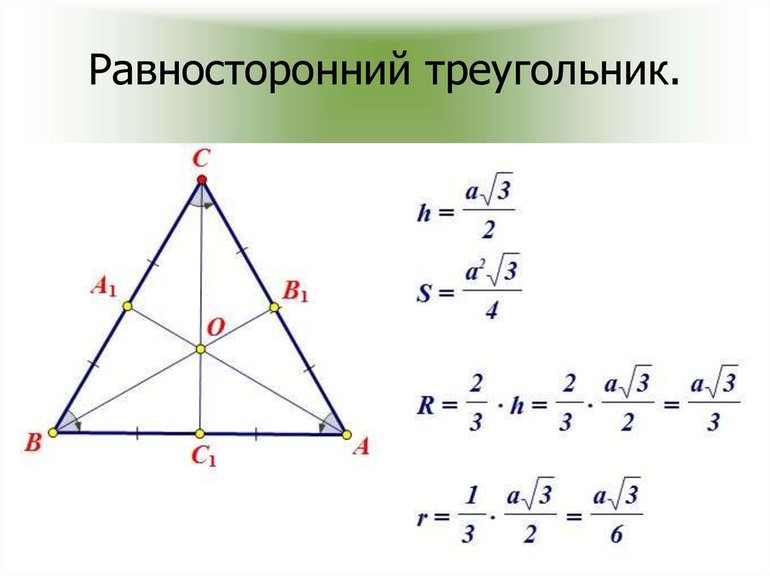
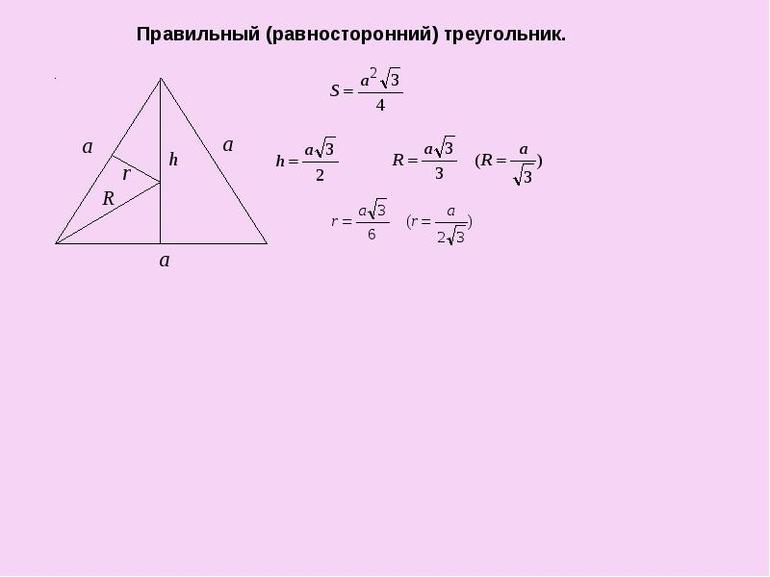
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √3) / 2.
Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √((2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √(2a — a) / (2a + a) = (a / 2) * √(1 / 3) = a / (2 * √3) = (a √3) / 6.
Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:
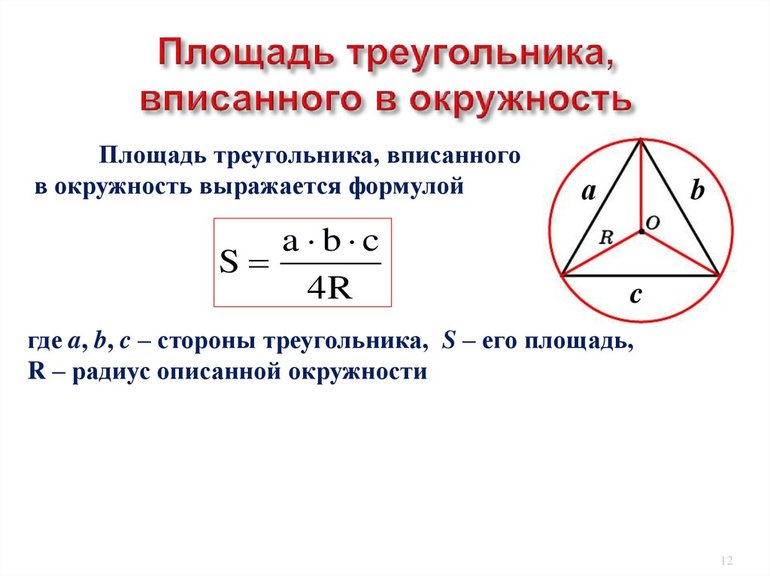
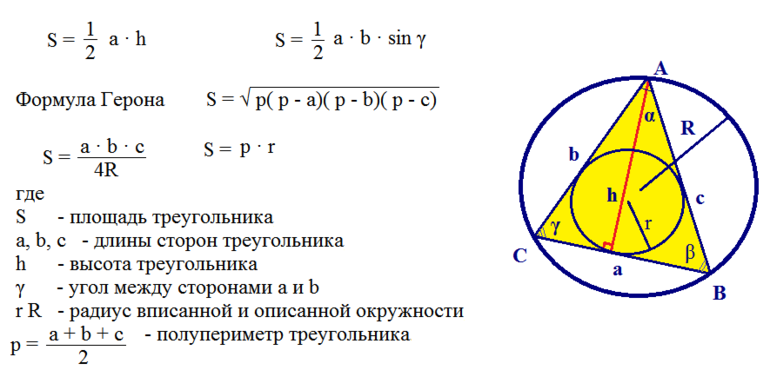
Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.
Решение задач
Чтобы уметь решать различные задания, связанные с треугольником, нужно помнить всего несколько формул. Но понадобится знать, что углы в фигуре равны друг другу и составляют 60 градусов. Часто придётся применять и теорему Пифагора. Вот некоторые из типовых заданий, используемые при обучении школьников в седьмом классе:
Проверить правильность решения, возможно, используя онлайн-калькуляторы. Это сервисы, которые предлагают бесплатно вычислить элементы правильной фигуры. При этом от пользователя требуется лишь внести в специальную форму исходные данные и нажать кнопку «Рассчитать».
Следует отметить, что выучить наизусть все формулы сложно, поэтому обычно используют логическое мышление и теоремы синусов-косинусов. Учитывая, что любой угол в равностороннем треугольнике равен 60 градусов практически любую формулу вывести можно самостоятельно.
| Равносторонний треугольник | |
|---|---|
 | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 3 |
| Символ Шлефли | |
| Диаграмма Кокстера |    |
| Группа симметрии | D 3 |
| Площадь | 3 4 а 2 <\ displaystyle <\ tfrac <\ sqrt <3>> <4>> а ^ <2>>  |
| Внутренний угол ( градусы ) | 60 ° |
СОДЕРЖАНИЕ
Основные свойства
Многие из этих величин имеют простую связь с высотой («h») каждой вершины с противоположной стороны:
В равностороннем треугольнике высота, биссектриса угла, середина перпендикуляра и медиана каждой стороны совпадают.
Характеристики
Стороны
Полупериметр
Площадь
Circumradius, inradius и exradii
Равные чевианы
Три вида чевианов совпадают и равны для равносторонних треугольников (и только для них):
Совпадающие центры треугольников
Шесть треугольников, образованных разбиением медианами
Для любого треугольника три медианы делят его на шесть меньших треугольников.
Очки в плоскости
Известные теоремы
Наглядное доказательство теоремы Вивиани
| 1. | Показаны ближайшие расстояния от точки P до сторон равностороннего треугольника ABC. |
| 2. | Линии DE, FG и HI, параллельные AB, BC и CA соответственно, определяют меньшие треугольники PHE, PFI и PDG. |
| 3. | Поскольку эти треугольники равносторонние, их высоту можно повернуть вертикально. |
| 4. | Поскольку PGCH представляет собой параллелограмм, треугольник PHE можно сдвинуть вверх, чтобы показать, что высота суммируется с высотой треугольника ABC. |
Теорема Морли о трехсекторах утверждает, что в любом треугольнике три точки пересечения смежных трехугольников образуют равносторонний треугольник.
Теорема Наполеона утверждает, что если равносторонние треугольники построены на сторонах любого треугольника, либо все наружу, либо все внутрь, центры этих равносторонних треугольников сами образуют равносторонний треугольник.
Версия изопериметрического неравенства для треугольников гласит, что треугольник наибольшей площади среди всех треугольников с заданным периметром является равносторонним.
Прочие свойства
По неравенству Эйлера равносторонний треугольник имеет наименьшее отношение R / r радиуса описанной окружности к внутреннему радиусу любого треугольника: в частности, R / r = 2.
Треугольник наибольшей площади из всех вписанных в данный круг равносторонний; и треугольник наименьшей площади из всех описанных вокруг данного круга является равносторонним.
Существует множество неравенств треугольника, которые выполняются с равенством тогда и только тогда, когда треугольник равносторонний.
Геометрическая конструкция
Вывод формулы площади
Формула площади в терминах длины стороны a может быть получена непосредственно с помощью теоремы Пифагора или с помощью тригонометрии. А знак равно 3 4 а 2 <\ displaystyle A = <\ frac <\ sqrt <3>> <4>> a ^ <2>>
Использование теоремы Пифагора
Площадь треугольника равна половине одной стороны а раз превышает высоту ч с той стороны:
Подстановка h в формулу площади (1/2) ah дает формулу площади равностороннего треугольника:
Использование тригонометрии
Каждый угол равностороннего треугольника равен 60 °, поэтому
так как все стороны равностороннего треугольника равны.
В культуре и обществе
Равносторонние треугольники часто появлялись в рукотворных конструкциях:
Признаки равенства треугольников
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Особенности, свойства, формулы и площадь равностороннего треугольника
равносторонний треугольник это многоугольник с тремя сторонами, где все равны; то есть они имеют одинаковую меру. Для этой характеристики ему было дано название равностороннего (равных сторон).
Характеристики равносторонних треугольников
Равные стороны
Равносторонние треугольники представляют собой плоские и замкнутые фигуры, состоящие из трех отрезков прямых линий. Треугольники классифицируются по их характеристикам по отношению к их сторонам и углам; равносторонний был классифицирован с использованием меры его сторон в качестве параметра, так как они абсолютно одинаковы, то есть они конгруэнтны.
Равносторонний треугольник является частным случаем равнобедренного треугольника, потому что две его стороны являются конгруэнтными. Вот почему все равносторонние треугольники также равнобедренные, но не все равнобедренные треугольники будут равносторонними.
Таким образом, равносторонние треугольники имеют одинаковые свойства равнобедренного треугольника..
компоненты
Треугольники в общем имеют несколько линий и точек, которые составляют его. Они используются для расчета площади, сторон, углов, медианы, биссектрисы, перпендикуляра и высоты.
В равностороннем треугольнике биссектриса оттянута от вершины угла к его противоположной стороне, разрезая это в его средней точке. Они совпадают в точке, называемой Incentro.
свойства
Таким образом, равносторонние треугольники унаследовали все свойства равнобедренного треугольника:
Внутренние углы
Внешние углы
Сумма сторон
Конгруэнтные стороны
Равносторонние треугольники имеют свои три стороны с одинаковой мерой или длиной; то есть они совпадают. Следовательно, в предыдущем пункте мы имеем a = b = c.
Конгруэнтные углы
Равносторонние треугольники также известны как равновеликие треугольники, потому что их три внутренних угла совпадают друг с другом. Это потому, что все его стороны также имеют одинаковую меру.
Биссектриса, медиана и медиатриса совпадают
Биссектриса делит сторону треугольника на две части. В равносторонних треугольниках эта сторона будет разделена на две абсолютно равные части, то есть треугольник будет разделен на два равных прямоугольных треугольника..
Таким образом, биссектриса, проведенная под любым углом равностороннего треугольника, совпадает с медианой и биссектрисой противоположной стороны этого угла.
пример:
На следующем рисунке показан треугольник ABC со средней точкой D, которая делит одну из его сторон на два сегмента AD и BD.
Когда вы рисуете линию от точки D к противоположной вершине, по определению вы получаете медиану CD, которая относится к вершине C и стороне AB.
Поскольку сегмент CD делит треугольник ABC на два треугольника, равных CDB и CDA, это означает, что у нас будет случай конгруэнции: сторона, угол, сторона и, следовательно, CD также будет биссектрисом BCD.
Сегмент CD образует углы, которые имеют одинаковые измерения для треугольников ADC и BDC, то есть они являются дополнительными таким образом, что измерение каждого из них будет:
Med. (ADB) + Med. (ADC) = 180 или
2 * Med. (ADC) = 180 или
Med. (ADC) = 180 или ÷ 2
Итак, у вас есть, что сегмент CD является также биссектрисом стороны AB.
Биссектриса и высота совпадают
Когда вы рисуете биссектрису от вершины угла до середины противоположной стороны, она делит равносторонний треугольник на два конгруэнтных треугольника..
Таким образом, что угол 90 образуется или (Прямой). Это указывает на то, что этот отрезок линии полностью перпендикулярен этой стороне, и по определению эта линия будет высотой.
Таким образом, биссектриса любого угла равностороннего треугольника совпадает с относительной высотой на противоположной стороне этого угла.
Ортоцентр, барицентр, стимулятор и круговой центр совпадают
Как рассчитать периметр?
Периметр многоугольника рассчитывается по сумме сторон. Поскольку в этом случае равносторонний треугольник имеет все стороны с одинаковой мерой, его периметр рассчитывается по следующей формуле:
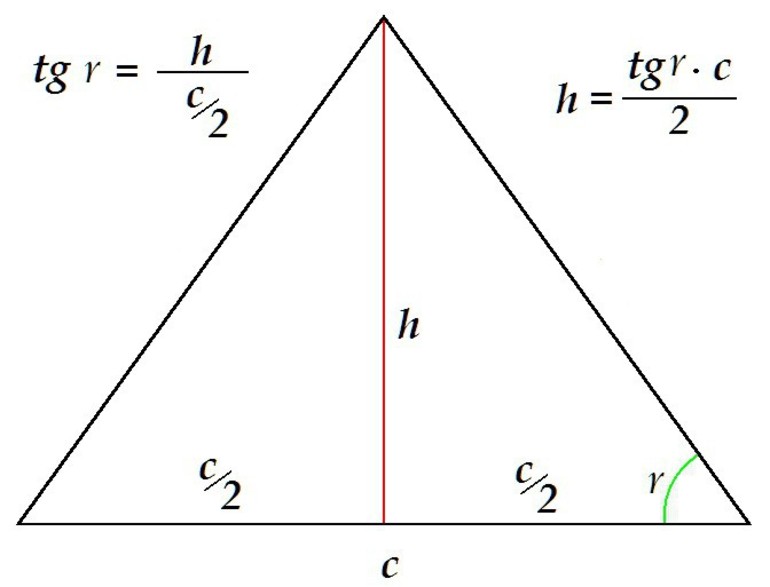
Как рассчитать высоту?
Высота (h) представляет противоположную сторону (a), половину стороны AC относительно соседней стороны (b), а сторона BC представляет гипотенузу (c).
Используя теорему Пифагора, вы можете определить значение высоты:
Подставляя эти значения в теорему Пифагора, и очищая высоту, мы имеем:
Если угол, образованный конгруэнтными сторонами, известен, высоту (представленную ногой) можно рассчитать, применяя тригонометрические соотношения.
Ноги называются противоположными или смежными в зависимости от угла, взятого за основу.
Например, на предыдущем рисунке катет h будет противоположен углу C, но прилегает к углу B:
Таким образом, высота может быть рассчитана с помощью:
Как рассчитать стороны?
Есть случаи, когда размеры сторон треугольника неизвестны, но их высота и углы, которые образуются в вершинах.
Для определения площади в этих случаях необходимо применять тригонометрические соотношения.
Зная угол одной из его вершин, ноги идентифицируются и используется соответствующее тригонометрическое соотношение:
Таким образом, ножка AB будет противоположной для угла C, но прилегающей к углу A. В зависимости от стороны или ножки, соответствующей высоте, другая сторона очищается для получения значения этого, зная, что в равностороннем треугольнике три стороны всегда будут иметь одинаковый размер.
Как рассчитать площадь?
Площадь треугольников всегда рассчитывается по одной и той же формуле, умножая основание на высоту и деля на два:
Зная, что высота дается по формуле:
обучение
Первое упражнение
Стороны равностороннего треугольника ABC размером 20 см каждая. Рассчитать высоту и площадь этого многоугольника.
решение
Чтобы определить площадь этого равностороннего треугольника, необходимо рассчитать высоту, зная, что при его рисовании он делит треугольник на два равных прямоугольных треугольника..
Таким образом, теорема Пифагора может быть использована для ее нахождения:
Данные в теореме заменяются:
100 см + б 2 = 400 см
То есть высота треугольника равна 17,32см. Теперь можно рассчитать площадь данного треугольника, подставив в формулу:
Площадь = (20 см * 17,32 см) ÷ 2
Площадь = 346,40 см 2 ÷ 2
Другим более простым способом решения упражнения является подстановка данных в прямую формулу области, где значение высоты также неявно:
Второе упражнение
На земле, которая имеет форму равностороннего треугольника, будут посажены цветы. Если периметр этой земли равен 450 м, рассчитайте количество квадратных метров, занимаемых цветами.
решение
Зная, что периметр треугольника соответствует сумме трех его сторон, и поскольку местность имеет форму равностороннего треугольника, три стороны этого треугольника будут иметь одинаковую меру или длину:
P = сторона + сторона + сторона = 3 * L
Теперь нужно только вычислить высоту этого треугольника..
Высота делит треугольник на два конгруэнтных прямоугольных треугольника, где одна из ножек представляет высоту, а другая половина основания. По теореме Пифагора высота может быть определена:
Данные в теореме заменяются:
(75 м) 2 + б 2 = (150 м) 2
5625 м + б 2 = 22 500 м
Таким образом, область, которая будет занимать цветы, будет:
Площадь = (150 м * 129,9 м) ÷ 2
Площадь = (19 485 м 2 ) ÷ 2
Площадь = 9 742,5 м 2
Третье упражнение
Равносторонний треугольник ABC разделен отрезком, который идет от его вершины C к средней точке D, расположенной на противоположной стороне (AB). Этот сегмент измеряет 62 метра. Рассчитать площадь и периметр этого равностороннего треугольника.
решение
Зная, что равносторонний треугольник разделен отрезком, соответствующим высоте, образуя два равных прямоугольных треугольника, это, в свою очередь, также делит угол вершины C на два угла с одинаковой мерой 30. или каждый.
Из этих данных можно определить значение одной из сторон треугольника, используя тригонометрические соотношения:
Поскольку в равностороннем треугольнике все стороны имеют одинаковую меру или длину, это означает, что каждая сторона равностороннего треугольника ABC равна 71,6 метра. Зная это, можно определить вашу область:
Площадь = (71,6 м * 62 м) ÷ 2
Площадь = 4 438,6 м 2 ÷ 2
Площадь = 2219,3 м 2
Периметр задается суммой трех его сторон:
P = сторона + сторона + сторона = 3 * L