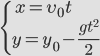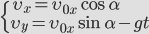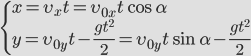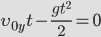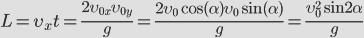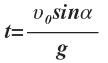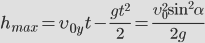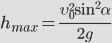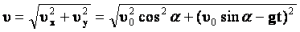как узнать дальность полета тела

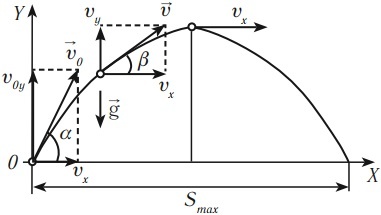
Как узнать дальность полета тела

Цель работы: изучение движения тела, брошенного под углом к горизонту; определение времени, дальности и высоты полета.

Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

где – начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

При нашем выборе начала координат начальные координаты (рис. 1) Тогда

(1)

Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:

.

(2)

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.

Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t₀. Подставляя значение (2) в первую формулу (1), получаем:

.

(3)

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.

Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

.

(4)

Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:

и подставить его во второе уравнение. Тогда получим:

Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.

Источник

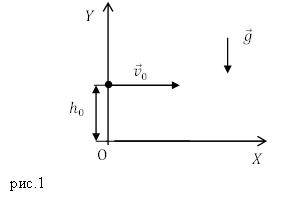
Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

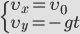
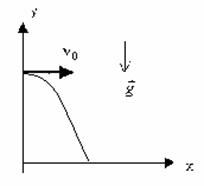
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

— между координатами квадратичная зависимость, траектория – парабола!

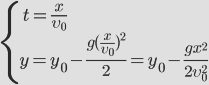
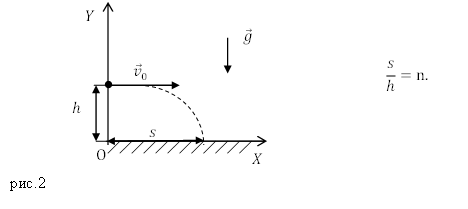
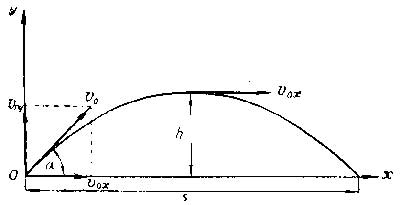
Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

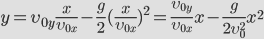
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Следовательно, для решения этой задачи необходимо решить уравнение

Зная время полета, найдем максимальное расстояние, которое пролетит тело:

Дальность полета:

Из этой формулы следует, что:

— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ;

— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.

Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Источник

Движение тела брошенного горизонтально

Постановка задачи. Начальные условия

Начальные условия при рассматриваемом нами движении точки:

Вектор ускорения при движении под действием силы тяжести считают постоянным:

так как \textit< >$\overline$ направлен вертикально вниз, то:

Кинематические уравнения движения тела брошенного горизонтально

Кинематическое уравнение для скорости равнопеременного движения в поле тяжести имеет вид:

В проекциях на оси координат получаем:

Модуль скорости движения точки при этом равен:

Уравнение для перемещения тела, брошенного горизонтально, запишем как:

Из системы уравнений (8) легко получить уравнение траектории движения точки, исключая из уравнений время:

Высшей точкой траектории движения тела в нашем случае является точка бросания.

Время полета тела брошенного горизонтально, дальность полета

Примеры задач с решением

Решение. Для решения задачи воспользуемся формулой, которую получили в теоретической части статьи, связывающую дальность полета тела и высоту, с которой это тело бросили горизонтально:

Воспользуемся условием, которое задано:

Выразим из формулы (1.1) искомую высоту, приняв во внимание (1.2), имеем:

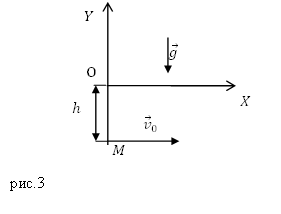
Задание. Напишите уравнения траектории движения материальной точки М для случая, который изображен на рис. 3.

Решение. Основой решения задачи служит кинематическое уравнение для перемещения при равноускоренном движении:

Спроектируем выражение (2.1) на оси X и Y:

Для того чтобы получить уравнение траектории выразим время из первого уравнения системы (2.2):

Подставим найденное время (2.3) во второе уравнение системы (2.3):

Источник

Движение тела, брошенного под углом к горизонту

Что такое движение тела брошенного под углом к горизонту

Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.

В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.

На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:

Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.

Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.

Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.

Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:

Зная следующие условия:

Записанная формула приобретает следующий вид:

Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.

Вывод формулы, как найти угол и дальность полета

Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:

Скорость тела будет рассчитываться таким образом:

Уравнение координаты записывают в следующем виде:

\(x=v_<0>\cos \alpha \times t\)

В любое время значения скорости тела будут равны:

Определить угол между вектором скорости и осью ОХ можно таким образом:

Время подъема на максимальную высоту составляет:

Максимальная высота подъема будет рассчитана следующим образом:

Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:

Максимальная дальность полета составит:

Примеры решения задач

Задача 1

Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.

Решение

Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:

Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:

Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.

Задача 2

Решение

Систему координат и движение тела можно представить схематично:

Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:

\(V_<0x>=V_ <0>\cos \alpha\) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.

В максимальной точке, на которую поднимется снаряд:

Из этого равенства следует:

Полное время полета тела будет рассчитано по формуле:

Дальность полета снаряда будет рассчитана таким образом:

Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.

Источник

Калькулятор движения снаряда

Наш калькулятор движения тела – это инструмент, который поможет вам проанализировать параболическое движение тела. Он может определить время полета, а также компоненты скорости, дальность полета и максимальную высоту полета. Продолжайте читать, если вы хотите понять, что такое движение тела, познакомьтесь с определением движения и определите вышеупомянутые значения с помощью уравнений движения тела.

Что такое движение тела (снаряда)? Определение движения снаряда

Анализ движения снаряда

Движение снаряда довольно логично. Предположим, вы знаете начальную скорость объекта V, угол запуска α и начальную высоту h. Наш калькулятор движения снаряда выполняет следующие действия, чтобы найти все оставшиеся параметры:

1. Вычислите составляющие скорости.

Три вектора – V, Vx и Vy – образуют прямоугольный треугольник.
Если вертикальная составляющая скорости равна 0, то это случай горизонтального движения снаряда. Если дополнительно α = 90 °, то это случай свободного падения.

2. Запишите уравнения движения.
Расстояние

3.Рассчитайте время полета.

t = 2 * Vy / g = 2 * V * sin (α) / g.

Однако, если мы бросаем объект с некоторой возвышенности, тогда формула не так хорошо сокращается, как раньше, и мы получаем квадратное уравнение для решения: h + Vy * t – g * t² / 2 = 0. После решения этой задачи уравнение, получаем:

t = [V * sin (α) + √ ((V * sin (α)) ² + 2 * g * h)] / g

4. Рассчитайте дальность полета снаряда.

График движения снаряда: дальность

Дальность полета снаряда – это общее горизонтальное расстояние, пройденное за время полета. Опять же, если мы запускаем объект с земли (начальная высота = 0), то мы можем записать формулу как R = Vx * t = Vx * 2 * Vy / g. Его также можно преобразовать в форму: R = V² * sin (2α) / g

Ситуация усложняется для начального значения высоты, отличного от 0. Затем нам нужно заменить длинную формулу из предыдущего шага на t:

R = Vx * t = V * cos (α) * [V * sin (α) + √ (V * sin (α)) ² + 2 * g * h)] / g

5. Рассчитайте максимальную высоту.

График движения снаряда: максимальная высота

Если Vy – g * t (Vy = 0) = 0, то мы можем переформулировать это уравнение к t (Vy = 0) = Vy / g.
Теперь мы просто находим расстояние по вертикали от земли в это время: hmax = Vy * t (vy = 0) – g * (t (Vy = 0)) ² / 2 = Vy² / (2 * g) = V² * sin (α) ² / (2 * г)
К счастью, в случае запуска снаряда с некоторой начальной высоты h нам нужно просто добавить это значение в окончательную формулу: hmax = h + V² * sin (α) ² / (2 * g)

Уравнения движения снаряда

Уфф, это было много вычислений! Подведем итог, чтобы сформировать наиболее важные уравнения движения снаряда:

Запуск объекта с земли (начальная высота h = 0)

Запуск объекта с некоторой высоты (начальная высота h> 0)

Использование нашего калькулятора движения снаряда наверняка сэкономит вам много времени. Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту и смотрите, как он выполняет все вычисления за вас!

Часто задаваемые вопросы

Нет, движение снаряда и его уравнения охватывают все движущиеся объекты, где единственной силой, действующей на них, является гравитация. Сюда входят объекты, которые подбрасываются прямо вверх, те, которые выбрасываются горизонтально, те, которые имеют горизонтальный и вертикальный компонент, и те, которые просто отбрасываются.

Как найти ускорение при движении снаряда?

Какие факторы влияют на движение снаряда, выпущенного горизонтально?

Каковы характеристики движения снаряда?

Свойства движения снаряда заключаются в том, что горизонтальная скорость объекта не изменяется, что его вертикальная скорость постоянно изменяется из-за силы тяжести, что форма его траектории будет параболой и что на объект не влияет сопротивление воздуха.

Кто первым и когда точно описал движение снаряда?

Галилей был первым человеком, который точно описал движение снаряда, разбив движение на горизонтальную и вертикальную составляющие и осознав, что график движения любого объекта всегда будет параболой. Он описал это в своей книге «О движении», опубликованной примерно в 1590-х годах.

Объект следует параболе из-за того, что гравитация влияет на две его составляющие движения – горизонтальную и вертикальную. Горизонтальная составляющая вообще не подвержена влиянию силы тяжести, поэтому изменяется линейно. Однако вертикальная часть постоянно находится под действием силы тяжести, поэтому она будет увеличиваться в высоте, а затем уменьшаться, ускоряясь под действием силы тяжести.

Почему 45 градусов – оптимальный угол для снарядов?

Уравнение для расстояния, пройденного снарядом под действием силы тяжести, имеет вид sin (2θ) v2 / g, где θ – угол, v – начальная скорость, а g – ускорение свободного падения. Предполагая, что v2 / g постоянна, наибольшее расстояние будет, когда sin (2θ) будет максимальным, то есть когда 2θ = 90 градусов. Это означает θ = 45 градусов.

Источник