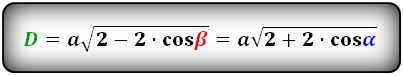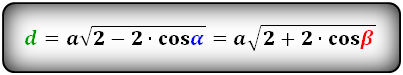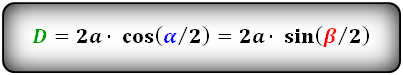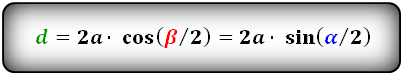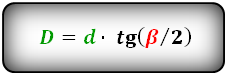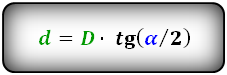как узнать диагональ ромба
Все формулы длины диагоналей ромба
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
Формулы диагоналей через сторону и угол, ( D d ):
Формулы диагоналей через сторону и половинный угол, ( D d ):
Формулы диагоналей через сторону и другую диагональ, ( D d ):
Формулы диагоналей через угол и другую диагональ, ( D d ):
Формулы диагоналей через площадь ( D d ):
Диагонали ромба
Свойства
Диагонали ромба обладают рядом особенностей, которые позволяют использовать их в вычислениях самих по себе. Во-первых, диагонали ромба пересекаются под прямым углом, что значит, что они образуют прямоугольные треугольники во внутреннем пространстве фигуры со стороной в качестве гипотенузы. Во-вторых, узнать длину катетов этих треугольников достаточно просто, так как точкой пересечения – вершиной прямого угла, диагонали делятся на две равные части. Подставив это в теорему Пифагора, можно найти сторону ромба как половину квадратного корня из произведения диагоналей. (рис.115.2) a=√(〖d_1〗^2+〖d_2〗^2 )/2
Угол напротив каждой диагонали можно найти из равнобедренных треугольников по теореме косинуса, заменив сторону ромба на полученный радикал. (рис.115.4) cosα=(〖2a〗^2-〖d_1〗^2)/〖2a〗^2 =((〖d_1〗^2+〖d_2〗^2)/2-〖d_1〗^2)/((〖d_1〗^2+〖d_2〗^2)/2)=(〖d_2〗^2-〖d_1〗^2)/(〖d_1〗^2+〖d_2〗^2 ) cosβ=(〖2a〗^2-〖d_2〗^2)/〖2a〗^2 =(〖d_1〗^2-〖d_2〗^2)/(〖d_1〗^2+〖d_2〗^2 )
Чтобы найти высоту ромба через диагонали, надо умножить выражение, соответствующее стороне на синус найденного угла, как отношение катета к гипотенузе в прямоугольном треугольнике. (рис.115.1) h=a sinα=sinα √(〖d_1〗^2+〖d_2〗^2 )/2
Периметр ромба будет равен радикалу стороны, умноженному на четыре (коэффициенты сокращаются, и остается два), а площадь – радикалу, возведенному в квадрат и умноженному на синус угла α. P=4a=2√(〖d_1〗^2+〖d_2〗^2 ) S=a^2 sinα=(sinα (〖d_1〗^2+〖d_2〗^2 ))/4
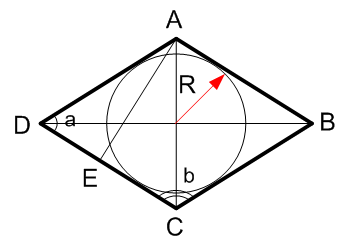
Радиус окружности, вписанной в ромб, представляет собой перпендикуляр стороны, проведенный к точке пересечения диагоналей, при продлении которой ровно в два раза получается высота ромба. Соответственно, чтобы найти радиус вписанной окружности через диагонали ромба, нужно разделить полученную формулу для высоты на два. (рис.115.3) r=h/2=sinα √(〖d_1〗^2+〖d_2〗^2 )/4
Формулы ромба
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
Признаки ромба
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
Длина стороны ромба через площадь (S) и синус угла
Длина стороны ромба через диагонали
Длина стороны ромба через диагональ и угол
Длина стороны ромба через периметр
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина диагонали ромба через сторону и другую диагональ
Длина диагонали ромба через площадь и другую диагональ
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
Площадь ромба через сторону и синус любого угла
Площадь ромба через две диагонали
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
Радиус вписанного круга в ромб через площадь и сторону ромба
Радиус вписанного круга в ромб через сторону и синус любого угла
Радиус вписанного круга в ромб через диагональ и синус угла
Радиус вписанного круга в ромб через две диагонали
Диагонали ромба
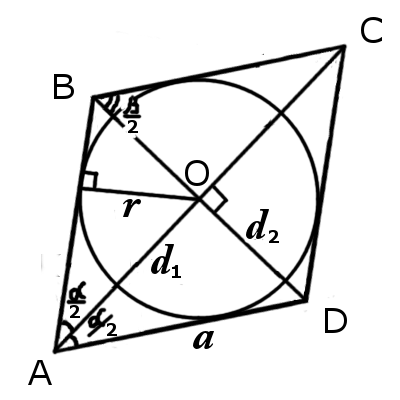
Ромб — частный случай параллелограмма, у которого все стороны равны, а противоположные — параллельны. Отрезки, соединяющие противоположные вершины ромба, называются его диагоналями. Они пересекаются между собой под прямым углом и делятся в точке пересечения пополам. Диагонали делят ромб на два равнобедренных треугольника и четыре одинаковых прямоугольных треугольника, у которых гипотенузой является сторона ромба (а), углом — половина угла ромба, сторонами (катетами) — половина диагоналей. Используя тригонометрические отношения находим катеты треугольника как произведение гипотенузы на синус и косинус половины известного угла. Чтобы найти второй угол, нужно из 180 градусов вычесть величину известного нам угла. Диагонали D, d ромба через сторону и половинный угол определяем по формуле:
где D — большая диагональ, d — меньшая диагональ ромба, a — сторона ромба, углы ромба α,β. Чтобы найти диагонали D, d через сторону и угол, воспользуемся формулами:
D = 2a × cos (α/2) = 2a × sin (β/2)
d = 2a × cos (β/2) = 2a × sin (α/2)
Если даны угол и сторона ромба, можно определить его высоту, как произведение стороны на синус угла. Произведение высоты на сторону ромба позволит определить его площадь. Площадь ромба через две его диагонали равна половине их произведений. Если известна площадь ромба и одна из его диагоналей, можно найти другую диагональ. Так как в ромбе все стороны равны, то его периметр равен произведению одной стороны на количество всех его сторон — четыре.
Ромб. Формулы, признаки и свойства ромба
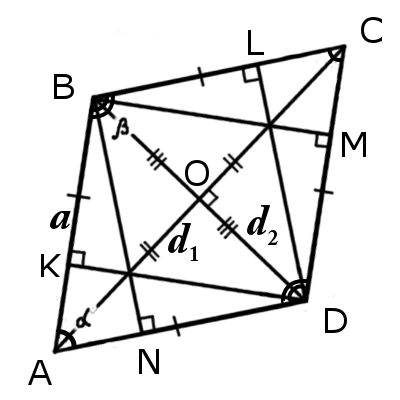 |  |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.