как узнать диагональ треугольника
Диагональ прямоугольника
Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.
Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.
Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.
Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.
Как найти диагональ прямоугольника
Воспользуемся теоремой Пифагора и формулой
d — диагональ квадрата
a — длина прямоугольника
b — ширина прямоугольника
Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.
Диагональ прямоугольника онлайн калькулятор
Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.
Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.
Диагональ треугольника
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
Рис. 1. Три медианы в треугольнике.
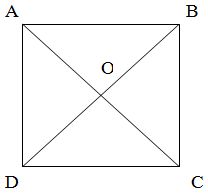
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=
Проверим для квадрата:
Рис. 3. Диагонали квадрата.
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
Геометрические фигуры. Прямоугольник. Формулы.
Диагонали прямоугольника.
Диагонали прямоугольника имеют одинаковую длину.
Диагонали прямоугольника делятся точкой пересечения пополам.
Длина диагонали прямоугольника можно вычислить по теореме Пифагора. И она равняется квадратному корню из суммы квадратов длины и ширины.
Формулы для вычисления длины диагонали прямоугольника:
1. Формула диагонали прямоугольника через 2 стороны прямоугольника (по теореме Пифагора):
2. Формула диагонали прямоугольника через площадь и сторону:
3. Формула диагонали прямоугольника через периметр и сторону:
4. Формула диагонали прямоугольника через радиус окружности (описанной):
5. Формула диагонали прямоугольника через диаметр окружности (описанной):
6. Формула диагонали прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:
7. Формула диагонали прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны, которая прилегает к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Признаки прямоугольника.
— Если диагонали его имеют одинаковую длину.
— Если квадрат диагонали параллелограмма равняется сумме квадратов смежных сторон.
— Если углы параллелограмма имеют одинаковую величину.
Стороны прямоугольника.
Формулы для определения длин сторон прямоугольника:
1. Формула стороны прямоугольника (длина и ширина прямоугольника) через диагональ и еще одну сторону:
2. Формула стороны прямоугольника (длина и ширина прямоугольника) через площадь и еще одну сторону:
3. Формула стороны прямоугольника (длина и ширина прямоугольника) через периметр и еще одну сторону:
4. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол α:
5. Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол β:
Окружность, описанная вокруг прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника:
1. Формула радиуса окружности, которая описана около прямоугольника через 2-е стороны:
2. Формула радиуса окружности, которая описана около прямоугольника через периметр квадрата и сторону:
3. Формула радиуса окружности, которая описана около прямоугольника через площадь квадрата:
4. Формула радиуса окружности, которая описана около прямоугольника через диагональ квадрата:
5. Формула радиуса окружности, которая описана около прямоугольника через диаметр окружности (описанной):
6. Формула радиуса окружности, которая описана около прямоугольника через синус угла, который прилегает к диагонали, и длину стороны противолежащей этому углу:
7. Формула радиуса окружности, которая описана около прямоугольника через косинус угла, который прилегает к диагонали, и длину стороны у этого угла:
8. Формула радиуса окружности, которая описана около прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника.
Формулы для определения угла между стороной и диагональю прямоугольника:
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника.
Формулы для определения угла меж диагоналей прямоугольника:
1. Формула определения угла меж диагоналей прямоугольника через угол между стороной и диагональю:
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Диагональ и сторона «А» прямоугольника
Свойства
В прямоугольнике диагональ со сторонами образует прямоугольный треугольник, который связывает все их значения вместе теоремой Пифагора. Поэтому неизвестную сторону можно выразить как квадратный корень из разности квадрата диагонали и квадрата известной стороны. (рис. 56.1) b=√(d^2-a^2 )
Тогда периметр прямоугольника и его площадь теперь будут зависеть только от одной стороны и диагонали, которые используя это выражение, можно подставить в любую необходимую формулу. P=2(a+b)=2(a+√(d^2-a^2 )) S=ab=a√(d^2-a^2 )
Угол пересечения диагонали со стороной зависит от отношения одной стороны к другой, которое образует тангенс искомого угла. Таким образом, меняя положение сторон в отношении, через арктангенс можно найти угол α и угол β. Опять же, вместо неизвестной стороны будет разность квадратов диагонали и стороны под корнем. α=arc tan〖b/a〗=arc tan〖√(d^2-a^2 )/a〗 β=arc tan〖a/b〗=arc tan〖a/√(d^2-a^2 )〗
Углы пересечения самих диагоналей делятся на две части, каждая из которых равна углу α или β з прямоугольного треугольника образованного полуосью симметрии прямоугольника. Поэтому, умножив нужный угол на 2, получим центральный угол прямоугольника. (рис. 56.2) γ=2α δ=2β
Также, зная диагональ, можно вычислить радиус описанной окружности. Диагонали в точке пересечения дают центр прямоугольника, который является и центром окружности. Соответственно радиус совпадает с диагональю, и равен ее половине. (рис. 56.3) R=d/2
Периметр и диагональ прямоугольника
Свойства
Зная периметр прямоугольника и его диагональ можно составить систему уравнений с двумя неизвестными, благодаря которой становится возможным решить задачу методом подстановки. (Рис.56.1) <█(P=2(a+b)@a^2+b^2=d^2 )┤
Чтобы решить такую систему, необходимо выразить одну сторону из первого уравнения. P=2(a+b) P=2a+2b 2a=P-2b a=P/2-b
Теперь полученное выражение для переменной «a» подставляем во второе уравнение и находим значение переменной «b». (P/2-b)^2+b^2=d^2 〖P^2/4-Pb+b^2+b〗^2=d^2 〖2b〗^2-Pb+P^2/4-d^2=0
Получилось квадратное уравнение, для решения которого нужно найти дискриминант. D=b^2-4ac=P^2-4*2*(P^2/4-d^2 )=P^2-2P^2+8d^2=8d^2-P^2
В данном уравнении при значении дискриминанта больше либо равном нулю 8d^2-P^2 ≥ 0, будет два решения. Это и будут обе стороны прямоугольника x=(-b±√(b^2-4ac))/2a b=(P+√(8d^2-P^2 ))/4 a=(P-√(8d^2-P^2 ))/4
Углы пересечения диагоналей со сторонами α и β можно найти из соотношения сторон в прямоугольном треугольнике, образованном диагональю. Тангенс угла α равен отношению b к a, а тангенс угла β равен отношению a к b. α=arc tan〖b/a〗 β=arc tan〖a/b〗
Вертикальные углы при пересечении диагоналей можно вычислить, удвоив величины углов α и β, как видно из рисунка. (рис. 56.2) γ=2α δ=2β
Радиус описанной окружности прямоугольника через диагональ вычисляется делением ее на два, так как точка пересечения диагоналей, которая является центром окружности, делит диагонали на две равные части – радиусы (рис. 56.3) R=d/2