как узнать объем цилиндра зная диаметр и высоту

26.06.202328.06.2023 admin 0 Comments

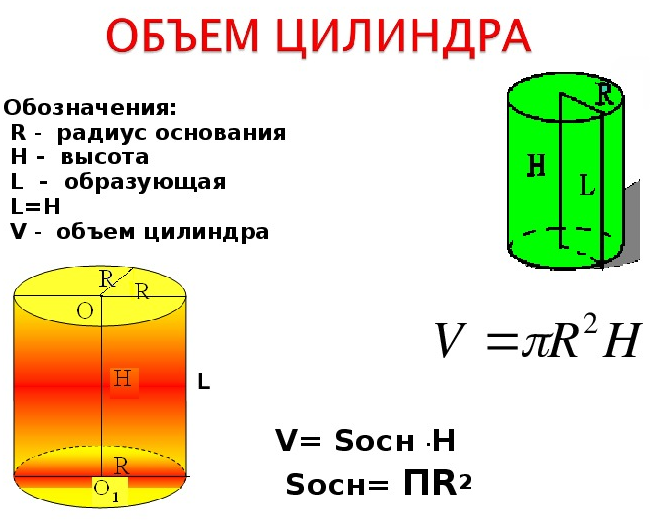
Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Объем правильного цилиндра через радиус и высоту цилиндра

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Цилиндр может быть правильным или наклонным .

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

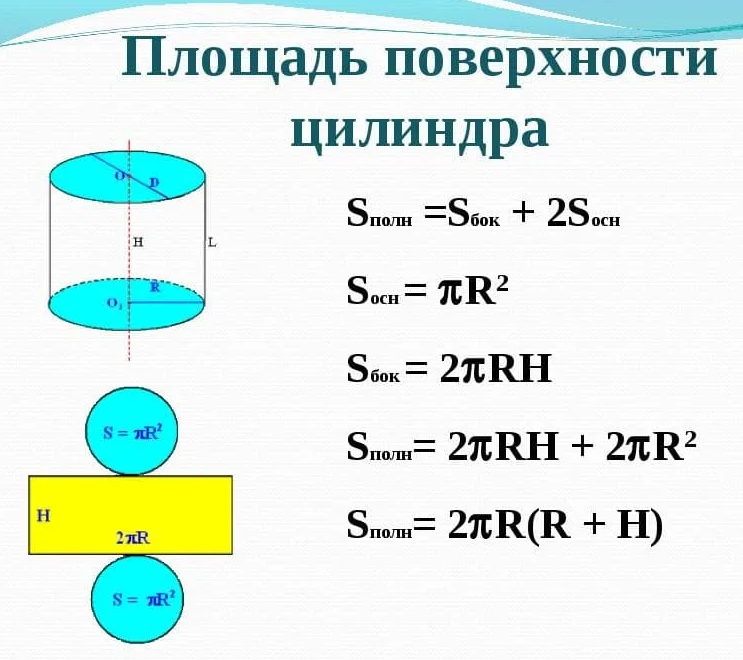
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .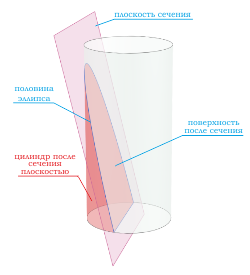

Что такое объем

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Источник

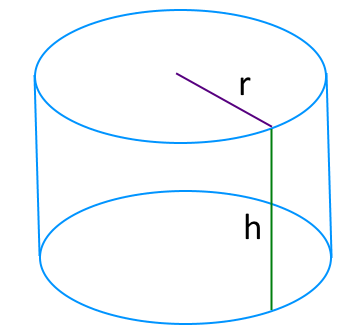
Диаметр и высота цилиндра

Свойства

Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD

Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD

Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD

Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD

Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD

Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2

Источник

Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба.

Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.

Как найти объем цилиндра

При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.

В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

Рассчитать его объем возможно следующим образом:

Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.

Формула объема цилиндра через диаметр

К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе.

В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:

Объем полого цилиндра

Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

Формула для вычисления:

r₁ 2 – внешний радиус;

r₂ 2 – внутренний радиус;

Примеры задач с решениями

Задача №1

Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?

Задача №2

В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.

Задача №3

На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см.

Сколько понадобится материала для изготовления труб?

Источник

Объем цилиндра — формулы и примеры расчетов

Как найти объем цилиндра

Рассчитать его объем возможно следующим образом:

Формула объема цилиндра через диаметр

Объем полого цилиндра

Формула для вычисления:

V = π (r 1 2 — r 2 2 )h

r1 2 – внешний радиус;

r2 2 – внутренний радиус;