как узнать площадь неправильного прямоугольника
Площадь неправильного четырехугольника
Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
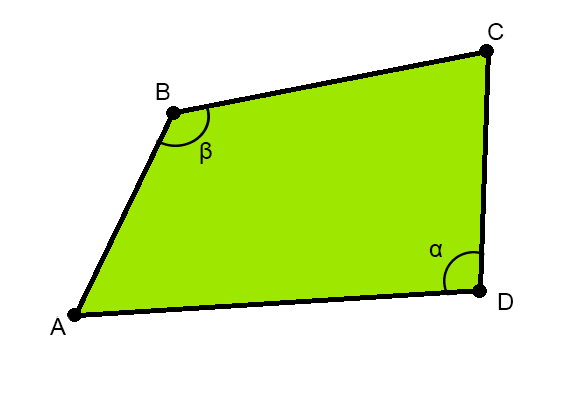
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
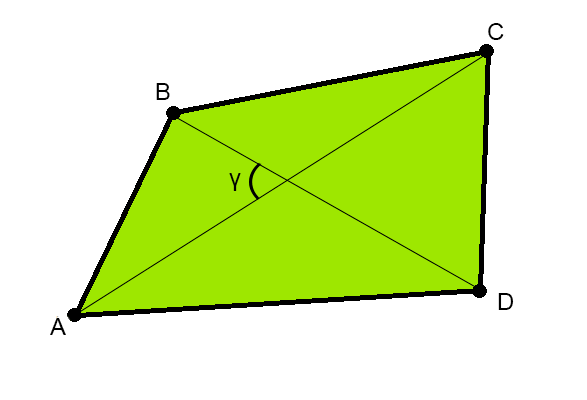
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | ||||||||||||||||||||||
| 1 | диагональ и угол между ними |  | ||||||||||||||||||||||
| 2 | стороны и углы между этими сторонами |  | Площадь частных случаев четырехугольниковДля вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта: ОпределенияЧетырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками. Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой. Расчет площади участкаИнструкция для калькулятора расчета площади земельного участка неправильной формы
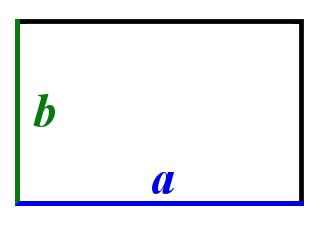
Впишите размеры сторон AB, BC, CD, DA в метрах. Замеры участка проводят, с помощью длинной рулетки, лазерного дальномера, мерного колеса. Также можно изготовить деревянную треногу (наподобие циркуля) зафиксировав расстоянием между «ногами» в 1 м и, шагая таким приспособлением вдоль границы делянки подсчитать количество шагов. Нажмите «Рассчитать». Онлайн калькулятор позволяет определить площадь (в квадратных метрах, сотках, акрах и гектарах) земельного участка или поля, имеющего неправильную форму. Это пригодится для корректного оформления документов права собственности на землю, продажи, сдачи в аренду или его деления (т.н. межевания) без применения топографической съемки и специальных картографических программ. Также иногда просто нужно посчитать сколько соток имеет участок, чтобы прикинуть его рыночную стоимость. Прямоугольник. Онлайн калькуляторС помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже. Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
Можно дать и другое определение прямоугольника. Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые. Свойства прямоугольникаТак как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника. Длиной прямоугольника называется более длинная пара его сторон. Шириной прямоугольника называется более короткая пара его сторон. Диагональ прямоугольникаОпределение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали. Для вычисления длины диагонали воспользуемся теоремой Пифагора:
Из равенства (1) найдем d: Пример 1. Стороны прямоугольника равны Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя
Ответ: Окружность, описанная около прямоугольникаОпределение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
Формула радиуса окружности описанной около прямоугольникаВыведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника. Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть Подставляя (3) в (2), получим: Пример 2. Стороны прямоугольника равны Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя
Ответ: Периметр прямоугольникаОпределение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P. Периметр прямоугольника вычисляется формулой: где \( \small a \) и \( \small b \) − стороны прямоугольника. Пример 3. Стороны прямоугольника равны Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя
Ответ: Формулы сторон прямоугольника через его диагональ и периметрВыведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника). Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем \( \small b \) и подставим в (6):
Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \): Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул: После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8). Примечание. Легко можно доказать, что Пример 4. Диагональ прямоугольника равна Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим
Подставляя значения
Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения
Ответ: Признаки прямоугольникаПризнак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником. Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником. Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником. Онлайн калькулятор. Площадь прямоугольникаИспользуя этот онлайн калькулятор, вы сможете найти площадь прямоугольника. Воспользовавшись онлайн калькулятором для вычисления площади прямоугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал. Найти площадь прямоугольникаВвод данных в калькулятор для вычисления площади прямоугольникаВ онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел. Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади прямоугольникаТеория. Площадь прямоугольникаФормула площади прямоугольника Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool.
|










 . Найти диагональ прямоугольника.
. Найти диагональ прямоугольника.


 . Найти радиус окружности, описанной вокруг прямоугольника.
. Найти радиус окружности, описанной вокруг прямоугольника.








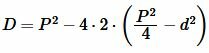
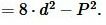
 , а периметр равен
, а периметр равен  . Найти стороны прямоугольника.
. Найти стороны прямоугольника.
 в первую формулу (12), получим:
в первую формулу (12), получим:
 в формулу, получим:
в формулу, получим:
 ,
,