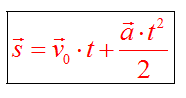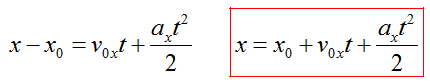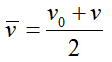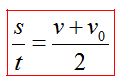как узнать путь при равноускоренном движении
04 — путь при равноускоренном движении
Путь при равноускоренном движении пропорционален квадрату времени движения. 
S — путь, пройденный телом, м
V0 — начальная скорость тела, м/c
a — ускорение, м/c 2
t — интервал движения, c
Во времена Галилео Галилея считалось, что легкие тела падают с высоты медленнее тяжелых. В 1589 году, Галилей выяснил, что тяжелые предметы падают вниз так же быстро, как и легкие. Чтобы проверить это предположение, он сбрасывал с Пизанской башни пушечное ядро и мушкетную пулю. Оба тела имели обтекаемую форму и достигали земли одновременно.

На основании своих экспериментов, Галилей вывел законы падения тел для случаев, когда сопротивлением воздуха можно пренебречь.
1. Все тела при падении движутся одинаково. Начав падать одновременно, они движутся с одинаковой скоростью.
2. Движение происходит с постоянным ускорением.
Подробности о равноускоренном движении тел можно узнать из этого видео с канала GetAClass.
Это важно запомнить — график пути при равноускоренном движении имеет форму параболы.
В этом видео рассказывается о том, как решать задачи по теме «движение тела, брошенного под углом к горизонту».
И еще одно видео о решении задач на тему «движение тела, брошенного под углом к горизонту».
Задача 4.
При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь.
Как посчитать путь ускоряющегося тела не используя время
Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.
Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).
Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.
Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.
Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.
Выводим формулу пути без времени
Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.
В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).
Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.
Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:
\( \large v_ <0>\left( \frac<\text<м>>
\( \large v \left( \frac<\text<м>>
\( \large a \left( \frac<\text<м>>
\( \large S \left( \text <м>\right)\) – путь, пройденный телом;
\(\large t \left( c \right)\) – время, за которое тело прошло этот путь.
В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.
Что сделать, чтобы получить формулу пути, в которой отсутствует время:
Выражаем время из формулы для скорости
Выпишем формулу, связывающую начальную и конечную скорость тела:
\[ \large v = v_ <0>+ a \cdot t \]
Избавимся в правой части от начальной скорости, обозначенной символом \( v_<0>\). Для этого из обеих частей уравнения вычтем число \( v_<0>\). Получим такую запись:
\[ \large v — v_ <0>= a \cdot t \]
Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:
Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».
В формулу пути подставим выражение для времени
Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:
В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:
Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.
Упрощаем выражение, расположенное до знака «плюс» в правой части
Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:
Умножим числитель дроби на число \(v_<0>\).
В числитель дроби, обособленный с помощью скобок помещаем число \(v_<0>\):
Теперь необходимо умножить скобку на число \(v_<0>\). На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.
Нужно к каждой скорости в скобках дописать число \(v_<0>\), умножая его на эти скорости. Получим такое выражение:
То есть, вместо первоначальной записи, мы получили такую запись:
Возводим в квадрат дробь
После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:
Правильно возвести дробь в степень поможет рисунок 3.
В результате возведения в квадрат дробь приобретет такой вид:
В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.
Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:
Теперь можем записать полученную дробь:
Упрощаем правую часть, записанную после знака «плюс»
Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:
Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:
Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.
Итак, поменяем местами знаменатели дробей:
Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:
А перемножив числители и знаменатели двух дробей, получим такую запись:
Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:
Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».
Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.
Приводим к общему знаменателю дроби в правой части уравнения
Вернемся еще раз к первоначальному уравнению:
Заменим правую часть этого уравнения выражениями, которые мы получили:
Сравним знаменатели дробей.
Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.
Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:
Примечания:
Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:
Получим такую дробь:
Поместим ее в выражение для пути:
Дроби с одинаковыми знаменателями складываем
Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:
Раскроем скобки в числителе полученного выражения:
Примечание: Обратим внимание на то, что в числителе дважды встречается член \(2v_ <0>v\), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа \(2v_<0>v\) вычитается такое же число \(2vv_<0>\). В конце концов, это число покидает нашу запись и, она упрощается:
Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:
Вычтем подобные члены, содержащие \( v^<2>_<0>\):
В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:
Примечания:
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
Выводы
Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:
I. Механика
Тестирование онлайн
Равноускоренное движение
Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Ускорение тела
Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
Упражнения
Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Какие из приведенных зависимостей описывают равноускоренное движение?
Уравнение скорости движущегося тела 
*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.