как узнать радиус кривой на жд пути
Ведомость расчета кривой
Расчет железнодорожной кривой
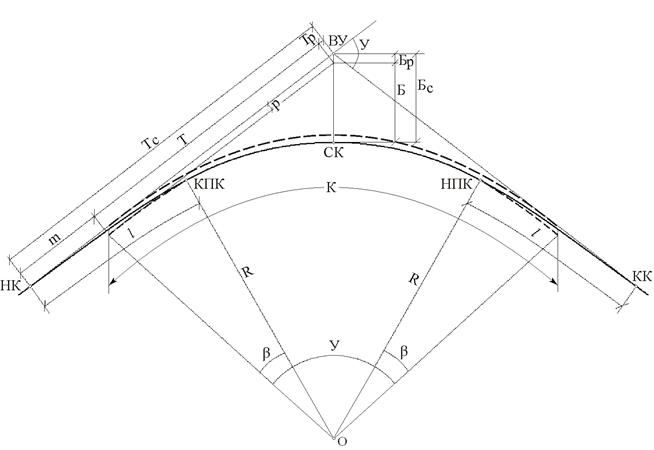
Железнодорожная кривая включает в себя круговую кривую и две переходные концевые кривые (рис.1). Переходные кривые обеспечивают плавный переход от прямого участка трассы на круговую кривую и обратно. Это достигается тем, что в пределах переходной кривой происходит постепенное изменение радиуса кривизны от r = ∞ (на стыке с прямой) до r = R (в точке КПК).
Расчет элементов кривой выполняют по углу поворота трассы У, радиусу круговой кривой R, длине переходной кривой l и пикетажному положению вершины угла поворота ПКВУ, которые выписывают из исходных данных. Угол поворота У измеряют теодолитом, радиусом кривой R и длиной переходной кривой l задаются согласно техническим условиям проектирования трассы, пикет вершины угла поворота ПКВУ выписывают из пикетажной книжки.
Суммированные элементы железнодорожной кривой вычисляют по формулам
Домер суммированный Дс— разность длины трассы на участке кривой по касательным и по кривой.
Элементы круговой и переходной кривой выбирают из таблиц для разбивки кривых на железных дорогах или рассчитывают по формулам
Угол поворота У в приведенных формулах выражают в долях градуса а элементы кривых вычисляют с точностью до 0,01м.
Вычислив элементы железнодорожной кривой, находят пикетажные положения ее главных точек НК, КК, СК
Контроль вычислений производят по формулам
Указанные вычисления выполняют в ведомости расчета кривой.
Ведомость расчета кривой
Кривая (поворот вправо)
Исходные данные: У=19°12¢, R = 800 м, l = 80 м.
| Т | 135,31 | К | 268,08 | Д | 2,54 | Б | 11,36 |
| Тр | 0,06 | l | 80,00 | Др | 0,12 | Бр | 0,34 |
| m | 40,00 | Кс | 348,08 | Дс | 2,66 | Бс | 11,70 |
| Тс | 175,37 |
2. Вычисление пикетажного положения главных точек кривой
| ВУ | ПК 17 + 35,90 | ВУ | ПК 17 + 35,90 |
| Тс | 1 75,37 | Тс | 1 75,37 |
| НК | 15 + 60,53 | 19 11,27 | |
| Кс | 3 48,08 | Дс | 2,66 |
| КК | 19 + 08,61 | КК | 19 + 08,61 |
| НК | 15 + 60,53 | ВУ | ПК 17 + 35,90 |
| Кс /2 | 1 74,04 | Дс /2 | 1,33 |
| СК | 17 + 34,57 | СК | 17 + 34,57 |
В контрольных вычислениях допускаются расхождения до 0,02 м.
Индивидуальное задание
1. Определите по таблицам для разбивки кривых на железных дорогах или вычислите по формулам значение всех элементов кривой. Произведите расчет пикетажа по трассе.
Исходные данные: У=21° аб¢, R = 600 м, l = 60 м, ВУ на ПК 27 + аб,аб
В исходные данные вместо аб подставить свой вариант (порядковый номер в учебном журнале).
Примеры: Вариант 07, У=21° 07¢, R = 600 м, l = 60 м, ВУ на ПК 27 + 07,07
Вариант 16, У=21°16¢, R = 600 м, l = 60 м, ВУ на ПК 27 + 16,16
2. На миллиметровой бумаге вычертите схему кривой с указанием всех элементов кривой и пикетажа.
3. Для детальной разбивки кривой способом прямоугольных координат определите для переходной и следующей за ней круговой кривой значения координат для длин (к), кратным 20 м (т.е. 20, 40, и т.д.) На миллиметровой бумаге в масштабе 1:1 000 вычертите схему детальной разбивки кривой.
Выполнение индивидуального задания
Вариант 32. Гр. СЖД – 25. Юшкевич А.С.
Ведомость расчета кривой
Кривая (поворот вправо)
Исходные данные: У=21°32¢, R = 600 м, l = 60 м.
Т= 114,18- 0.09=114.09 Тр= 0,05
К= 225,67- 0.17=225.50 m = 30,00
| Т | 114,09 | К | 225,50 | Д | 2,69 | Б | 10,75 |
| Тр | 0,05 | l | 60,00 | Др | 0,10 | Бр | 0,25 |
| m | 30,00 | Кс | 285,50 | Дс | 2,79 | Бс | 11,00 |
| Тс | 144,14 |
2. Вычисление пикетажного положения главных точек кривой
| ВУ | ПК 27 + 32,32 | ВУ | ПК 27 + 32,32 |
| Тс | 1 44,14 | Тс | 1 44,14 |
| НК | 25 + 88,18 | 28 76,46 | |
| Кс | 2 85,50 | Дс | 2,79 |
| КК | 28 + 73,68 | КК | 28 + 73,67 |
| НК | 25 + 88,18 | ВУ | ПК 27 + 32,32 |
| Кс /2 | 1 42,75 | Дс /2 | 1,40 |
| СК | 27 + 30,93 | СК | 27 + 30,92 |
В контрольных вычислениях допускаются расхождения до 0,02 м.
На миллиметровой бумаге вычерчиваю схему кривой с указанием всех элементов кривой и пикетажа.
Выписываю координаты для переходной и следующей за ней круговой кривой для детальной разбивки кривой способом прямоугольных координат.
У=21°32¢, R = 600 м, l = 60 м.
| к | к-х | у | к | к-х | у |
| 0.00 | 0.04 | 0.16 | 4.33 | ||
| 0.00 | 0.30 | 0.34 | 6.99 | ||
| 0.02 | 1.00 | 0.62 | 10.31 | ||
| 0.06 | 2.33 | Тс = 144,14 |
На миллиметровой бумаге в масштабе 1:1 000 вычерчиваю схему детальной разбивки кривой.
Расчет выправки железнодорожных кривых (Раздел дипломной работы на тему: «Организация контроля состояния пути. Оценка и приведение кривых к расчетным параметрам»)
Страницы работы
Содержание работы
10 Расчет выправки железнодорожных кривых
Как бы идеально правильно ни была уложена в плане кривая, после прохождения определенного количества поездов ее геометрические очертания будут неизбежно нарушены или, как говорят, «кривая будет сбита». В первую очередь это относится к кривым с малыми радиусами, а также к кривым, имеющим непостоянный радиус. При этом кривые наиболее нарушены в условиях повышенных скоростей движения, слабых балластов и рельсошпальной решетки, когда путь недостаточно устойчив, а воздействие подвижного состава на него велико.
Работы по выправке кривых заключаются в отрихтовывании их в геометрически правильное положение, возможно и отличное от первоначального проектного, и связаны со специальным расчетом. Целью расчета является определение удовлетворяющих условиям задачи сдвигов, или рихтовок, в ряде точек кривой, необходимых для придания кривой правильного положения.
Под правильным положением кривой в плане следует понимать соблюдение плавности переходных кривых и постоянства радиуса кругового участка. Если кривая составлена из участков различных радиусов, должен быть обеспечен плавный переход от одного радиуса к другому.
Весь комплекс работ по выправке расстроенных кривых состоит из следующих основных этапов: съемки существующей натурной кривой, расчета рихтовок, или сдвигов, подготовки и производства самой рихтовки или постановки кривой в проектное положение.
Исходными материалами для расчета выправки кривой являются данные, полученные при съемке кривой. Процесс съемки заключается в измерении в определенных местах кривой так называемых стрел прогиба. Для этого вся кривая делится на равные участки длиной по 10 м при радиусе кривой R > 400 м или 5 м при R 1 2
как измерить радиус кривой? подскажите





Попробуйте так!
При длине кривой, определяемой не по оси дороги, а по кромке проезжей части, найденное значение радиуса уточняется:
где RK — уточненный радиус кривой, м; R — вычисленное значение радиуса, м; В — ширина проезжей части, м.
По второму способу радиус кривой определяют путем измерения отрезка Z хорды l1 стягивающей дугу окружности (рис. 7.3).
Хорду рекомендуется принимать равной длине мерной ленты (20 м). Радиус кривой в плане определяют по формуле:
Как и по первому способу, при определении длин стрелки Z хорды l1 по кромке покрытия радиус кривой уточняется.
По третьему способу вначале определяют вершину угла поворота. Затем с помощью теодолита, установленного над точкой вершины угла, определяют угол поворота и длину отрезка биссектрисы, измеряемой мерной лентой или курвиметром от вершины угла поворота до середины проезжей части (рис. 7.4).
Рис. 7.3. Схема для определения радиуса кривой по хорде: l1 — хорда; Z — отрезок; остальные обозначения см. на рис. 7.2
Рис. 7.4. Схема для определения радиуса кривой по биссектрисе:
— длина отрезка биссектрисы от вершины угла до середины проезжей части; остальные обозначения см. на рис. 7.2
Радиус кривой определяют по формуле:
где l2 — длина отрезка биссектрисы от вершины угла поворота до середины проезжей части, м.
Для определения расстояния видимости используют геодезические приборы (теодолит, дальномер и дальномерные насадки).
При наличии чертежей плана и продольного профиля расстояние видимости может быть установлено графоаналитическими методами. В этом случае расстояние видимости в продольном профиле измеряют с помощью специального прибора (рис. 7.5). Прибор состоит из опорной плиты 1 и линейки 2, поворачивающейся вокруг точек А и В. На плите нанесена шкала расстояний 6 в масштабе 1:5000. На окружностях 5, имеющих центры в точках An В, нанесены шкалы уклонов, дающие возможность внесения поправок на ошибки при измерении расстояний видимости, вызываемые тем, что вертикальный масштаб профилей в 10 раз превышает их горизонтальный масштаб. Поправку следует вводить при уклонах более 40 %.





как измерить радиус кривой? подскажите Ответить в теме




















Всем привет! Могу предложить такой вариант расчёта.
Вложения
 | Стрела изгиба КК и ПКК.xls (19.5 Кб, 1371 просмотров) |





Кривые малого радиуса измеряют хордой 10м.
Как измерять показано в файле Промер стрел изгиба.gif

Вложения
 | кривые образец.xls (81.0 Кб, 1250 просмотров) |















Что за цифра 5000?
Как уже было сказано выше, на практике пользуются шнурами длиной 20 м. Формула связи радиуса, хорды и стрелы прогиба была дана выше.
Стрелу прогиба измеряют в см, а в 1 м их 100, т.к. что цифра 5000 образовалась от возведения в квадрат числа 20, что составит 400, и деления его на 8, что составит 50. Далее домножаем на 100 в соответствии с теорией размерности и делим на величина стрелы прогиба (см), получая значения радиуса в метрах.
Могу предложить другие методы определения и их теоретическое обоснование. По фото наиболее удобны для определения кривые радиусами 800 и 600 м, если хорду берём между двумя точками соседних пикетов по внутренним краям внешнего рельса. 100*100/(8*800)=1,56 м, т.е. при 800 м радиусе (в дуге 100 м) хорода будет проходить ровно через середину внутреннего рельса.










Где фото?
Извините, вы о том фото, что автор темы предъявить должен был, или о тех, что я в своём сообщении говорил? Если да, то приведу, только скажите, что именно. А то я прежде всего имел в виду примеры с самыми удобными в плане определения по фото (при наличии или видимости пикетных меток, конечно же) радиусами 600 и 800 м.
Scobaru добавил 22.08.2016 в 22:40
[quote=flexfirst;236484]Кривые малого радиуса измеряют хордой 10м.
Да, чем круче кривая, тем меньше нужна хорда, т.к. стрела прогиба при 20 м увеличивается, и увеличивается погрешность. А почему?
А давайте вспомним родную математику, а именно геометрию и тригонометрию.
Как узнать радиус кривой на жд пути
При длине кривой, определяемой не по оси дороги, а по кромке проезжей части, найденное значение радиуса уточняется:
где RK — уточненный радиус кривой, м; R — вычисленное значение радиуса, м; В — ширина проезжей части, м.
По второму способу радиус кривой определяют путем измерения отрезка Z хорды l1 стягивающей дугу окружности (рис. 7.3).
Хорду рекомендуется принимать равной длине мерной ленты (20 м). Радиус кривой в плане определяют по формуле:
Как и по первому способу, при определении длин стрелки Z хорды l1 по кромке покрытия радиус кривой уточняется.
По третьему способу вначале определяют вершину угла поворота. Затем с помощью теодолита, установленного над точкой вершины угла, определяют угол поворота и длину отрезка биссектрисы, измеряемой мерной лентой или курвиметром от вершины угла поворота до середины проезжей части (рис. 7.4).
Рис. 7.3. Схема для определения радиуса кривой по хорде: l1 — хорда; Z — отрезок; остальные обозначения см. на рис. 7.2
Рис. 7.4. Схема для определения радиуса кривой по биссектрисе:
— длина отрезка биссектрисы от вершины угла до середины проезжей части; остальные обозначения см. на рис. 7.2
Радиус кривой определяют по формуле:
где l2 — длина отрезка биссектрисы от вершины угла поворота до середины проезжей части, м.
Для определения расстояния видимости используют геодезические приборы (теодолит, дальномер и дальномерные насадки).
При наличии чертежей плана и продольного профиля расстояние видимости может быть установлено графоаналитическими методами. В этом случае расстояние видимости в продольном профиле измеряют с помощью специального прибора (рис. 7.5). Прибор состоит из опорной плиты 1 и линейки 2, поворачивающейся вокруг точек А и В. На плите нанесена шкала расстояний 6 в масштабе 1:5000. На окружностях 5, имеющих центры в точках An В, нанесены шкалы уклонов, дающие возможность внесения поправок на ошибки при измерении расстояний видимости, вызываемые тем, что вертикальный масштаб профилей в 10 раз превышает их горизонтальный масштаб. Поправку следует вводить при уклонах более 40 %.
Всем привет! Могу предложить такой вариант расчёта.
Кривые малого радиуса измеряют хордой 10м.
Как измерять показано в файле Промер стрел изгиба.gif
Как уже было сказано выше, на практике пользуются шнурами длиной 20 м. Формула связи радиуса, хорды и стрелы прогиба была дана выше.
Стрелу прогиба измеряют в см, а в 1 м их 100, т.к. что цифра 5000 образовалась от возведения в квадрат числа 20, что составит 400, и деления его на 8, что составит 50. Далее домножаем на 100 в соответствии с теорией размерности и делим на величина стрелы прогиба (см), получая значения радиуса в метрах.
Могу предложить другие методы определения и их теоретическое обоснование. По фото наиболее удобны для определения кривые радиусами 800 и 600 м, если хорду берём между двумя точками соседних пикетов по внутренним краям внешнего рельса. 100*100/(8*800)=1,56 м, т.е. при 800 м радиусе (в дуге 100 м) хорода будет проходить ровно через середину внутреннего рельса.
Извините, вы о том фото, что автор темы предъявить должен был, или о тех, что я в своём сообщении говорил? Если да, то приведу, только скажите, что именно. А то я прежде всего имел в виду примеры с самыми удобными в плане определения по фото (при наличии или видимости пикетных меток, конечно же) радиусами 600 и 800 м.
Scobaru добавил 22.08.2016 в 22:40
[quote=flexfirst;236484]Кривые малого радиуса измеряют хордой 10м.
Да, чем круче кривая, тем меньше нужна хорда, т.к. стрела прогиба при 20 м увеличивается, и увеличивается погрешность. А почему?
А давайте вспомним родную математику, а именно геометрию и тригонометрию.
Как узнать радиус кривой на жд пути
§ 4. Содержание кривых участков пути в плане
В кривых путь работает более напряженно, чем прямых. Объясняется это тем, что при движении экипажа по кривой на рельсы передаются дополнительные силы: неуравновешенная возвышением часть центробежной силы и силы рамного давления от вписывания жесткой базы подвижного состава в колею.
Влияние этих дополнительных сил на работу пути и экипажа о многом зависит от состояния кривых в плане. При непостоянной кривизне круговой кривой и неплавном изменении кривизны в переходных кривых возникают большие горизонтальные неуравновешенные силы, вызывающие резкие боковые толчки подвижного состава, дополнительные напряжения в элементах пути, а, следовательно, и более усиленные расстройства его.
Положение рельсовой колеи в плане в кривой характеризуется стрелами изгиба кривой, измеряемыми от хорды определенной длины.
Идеально поставленная круговая кривая на всем своем протяжении в любой точке должна иметь одну и ту же стрелу изгиба.
При текущем содержании состояние кривых участков главных и приемоотправочных путей признается удовлетворительным, если разность соседних стрел в точках через 10 м при хорде в 20 м не превышает указанных в табл. 3 величин.
Таблица 3. Допуски в содержании кривых в плане
Правильное содержание кривых в плане заключается в периодической проверке кривизны измерением стрел, в сравнении полученных стрел с паспортными и в случае расхождения, с учетом допусков, в приведении стрел к паспортным рихтовкой пути.
Величина эвольвенты Еп с достаточной для практических целей точностью может быть определена через величину стрел изгиба fi (рис. 17). Например, эвольвента точки 4 определится как
что можно видеть, если просуммировать дважды ряд соответствующих стрел (табл. 4).
Таблица 4. Расчет эвольвент
В общем виде длина эвольвенты любой точки кривой определится как
Чтобы найти величину сдвижки в заданной точке n, достаточно определить разность эвольвент натурной и проектной кривых
Рис. 16. Зависимость между эвольвентами и величинами сдвижек
Отсюда вытекает, что разница в величине эвольвент, т. е. величина сдвижки любой точки кривой из сбитого (натурного) положения в проектное, равна удвоенной сумме сумм разностей натурных и проектных стрел кривой, взятых по всем точкам от начала кривой до рассматриваемой точки. В таком виде вывод расчетной формулы впервые дан проф. П. Г. Козийчуком (см. П. Г. Козийчук «Расчет кривых железнодорожного пути графо-аналитическим методом». Трансжелдориздат, 1946).
Рис. 17. Эвольвента круга и зависимость ее от величины стрел изгиба
В расчетах выправки кривых используется также зависимость между величинами стрел, измеренных от одинаковых хорд, и углом поворота кривой.
Рис. 18. Влияние сдвижки кривой в какой-либо точке на стрелы изгиба в соседних точках
Рис. 19. Зависимость между углом поворота кривой и стрелами изгиба
Исходя из того что в треугольнике внешний угол равен сумме двух внутренних, с ним не смежных, и учитывая, что треугольники в данном случае будут равнобедренными, получаем:
а угол поворота всей кривой 
С другой стороны, вследствие малости углов поворота на протяжении длины дуги, стягиваемой хордой (обычно длиной 20 м), с допустимой неточностью можно принять (считая 1 за длину хорды одного деления):
Следовательно, угол поворота на протяжении всей кривой
Поскольку общий угол φ поворота каждой данной кривой остается постоянным независимо от того, правильно стоит кривая или часть ее сдвинулась наружу, а часть внутрь, и поскольку кривая каждый раз разбивается на деления одинаковой длины, т. е. длина хорд постоянно равна l, то из приведенной зависимости вытекает, что сумма стрел тоже всегда будет одной и той же.
В самом деле, если измеренные стрелы обозначены через fi, а после выправки через Fi, будем иметь
На отечественных дорогах применяется ряд способов расчета выправки кривых, в которых величины сдвижек подсчитываются по разности эвольвент. Эти способы отличаются друг от друга приемами определения проектных стрел. На основе изучения и практического сопоставления различных способов расчета выправки кривых Главным управлением пути МПС рекомендованы для практического применения на сети дорог графические и графоаналитические способы, разработанные инженерами М. А. Макуровым, А. Т. Крагелем, М. Д. Поликарповым, а также способ последовательного приближения с применением прибора доцента И. Я. Туровского.
Графический способ расчета выправки кривых, предложенный инж. А. Т. Крагелем, основан на теории проф. П. Г. Козийчука. Вычисления в этом способе расчета заменены графическими построениями при помощи циркуля-измерителя.
Инж. М. А. Макуров предложил способ расчета выправки кривых, основанный тоже на разности стрел, но по принципу проектирования проектных стрел отличающийся от способа проф. П. Г. Козийчука тем, что вариант выправки кривой выбирается не по графику стрел, а по графику суммы стрел.
Инж. М. Д. Поликарпов дополнил способ проф. Козийчука приемами, обеспечивающими более наглядный выбор наилучшего варианта проектного положения кривой.
Ниже подробно рассматривается способ инж. М. Д. Поликарпова, получивший наибольшее распространение. Исходными материалами для расчета выправки кривой являются данные, полученные при съемке кривой.
Стрелы измеряют в каждой точке деления при хорде, равной двум делениям. Шнур, применяемый в качестве хорды, должен быть тонким, крепким, без узлов в местах касания к рельсу, длиной несколько большей двух делений. Для большей точности промеров полезно применять шнур из тонкой проволоки диаметром 0,25 мм и струбцину ЦНИИ (рис. 20) для натяжения шнура.
Шнур прижимают к незакругленной части рабочей грани головки рельса против меток, смежных с той, где измеряется стрела. Перед измерением стрелы колебание шнура надо остановить. Стрелы отсчитывают по стороне шнура, обращенной к рельсу, с точностью до 1 мм.
Если у входа или выхода из кривой имеется обратный изгиб кривой (когда вход «отбит» наружу), то стрелы этого обратного изгиба записывают со знаком минус. Концы шнура в этом случае прижимают к нерабочей грани рельса за пределами наплыва.
Кроме стрел, измеряют расстояния от оси пути до бровки земляного полотна и до всех близко стоящих сооружений, устройств. На двухпутных участках измеряют расстояния между осями путей. По этим данным определяют точки, не подлежащие сдвигу и имеющие ограничения по сдвигу в зависимости от ширины обочин земляного полотна, наличия искусственных сооружений и других местных условий (переезды, стрелки и др.).
Результаты промеров и привязки мест промеров к километрам и пикетам записывают в журнале съемки кривой.
Для обеспечения необходимой точности расчетов стрелы измеряют дважды, при этом проверяют, чтобы сумма измеренных стрел не отличалась от суммы паспортных более чем на ±0,5%.
Расчет выправки кривых не имеет сразу прямого решения, а выполняется поэтапно, в большей степени методом последовательного приближения.
Первый этап расчета заключается в том, что на основании имеющихся натурных стрел задаются расчетными стрелами, при которых кривая будет правильной, и проверяют, удовлетворяет ли она требованиям, предъявляемым к выправленной кривой, или нет. В последнем случае, что, как правило, и бывает на практике, производят второй этап расчета кривой, который состоит в том, что в первый вариант расчетных стрел вносят определенные коррективы, позволяющие прийти к удовлетворительному решению.
В качестве примера приводится расчет выправки сбитой кривой, имеющей длину 170 м (вместе с переходными кривыми).
Первый вариант проектных стрел намечают на графике натурных и проектных стрел (рис. 21).
За ось графика натурных стрел принимается одна из утолщенных горизонтальных линий сетки. Под осью графика помещаются три горизонтальные графы: для натурных, расчетных и проектных стрел и строка для номеров точек делений кривой.
Если начало переходной кривой (НПК) и конец переходной кривой (КПК) совпадают с точками деления кривой, то стрелы в этих точках определяются по формулам проф. П. Г. Козийчука: стрела в НПК равна
стрела в КПК равна
Для рассматриваемого примера стрелы будут иметь следующие значения: стрела в НПК
После того как график расчетных стрел построен, в соответствующую графу графика выписываются определяемые по графику численные значения расчетных стрел для каждой точки кривой и подсчитывается их сумма. Сумма расчетных стрел должна равняться сумме натурных стрел. Если эти суммы не равны, то расчетные стрелы следует изменить так, чтобы это равенство было достигнуто и при этом не была нарушена плавность кривой.
В данном примере для соблюдения равенства сумм стрел в точке № 17 расчетная стрела была увеличена на 1 мм против первоначального значения.
Полученные расчетные и натурные стрелы заносятся в специальную расчетную таблицу (табл. 5), имеющую 14 граф.
Таблица 5. Расчет выправки кривой
В графу 5 вписывается нарастающим итогом алгебраическая сумма разностей стрел для каждой точки деления. В первой строке графы 5 пишется нуль; во второй строке пишется число второй строки графы 4, к нему прибавляется число третьей строки графы 4 и результат записывается в третью строку графы 5 и т. д. (в таблице показано стрелками).
В графу 6 нарастающим итогом вписывается алгебраическая сумма сумм (расчетный полусдвиг) разностей стрел. Во второй строке пишется нуль; к нему прибавляется число второй строки графы 5 и результат записывается в третью строку графы 6, затем к полученному прибавляется число третьей строки графы 5 и результат записывается в четвертую строку графы 6 и т. д. (в таблице это показано стрелками). Величина полусдвига в последней строке графы 6 должна равняться итогу графы 5, что является контролем подсчета графы 6.
Для того чтобы было выполнено это условие, необходимо в первый вариант расчетных стрел внести некоторые коррективы.
Корректировка расчетных стрел и, следовательно, сдвижек производится с помощью графика полусдвигов (рис. 22).
Между начальной и конечной точками проектная линия 2 может проходить как угодно (со спусками и подъемами). Это зависит от желания получить те или иные сдвиги, учитывая, что расстояния от проектной линии до линии графика расчетных полусдвигов 1 есть величины проектных полусдвигов.
Проектная линия не должна выходить за пределы возможных (по местным условиям) сдвигов, тогда проектные сдвиги будут везде допустимыми.
Так, величина наклона проектной линии между точками 1 и 4 равна
между точками 9 и 13 равна
В рассматриваемом примере: +3-3-6+3+2+1=0.
Общие поправки выписываются в соответствующую графу графика полусдвигов (рис. 22), а затем в графу 7 табл. 5.
Общие поправки почти всегда оказываются значительных размеров и потому их приходится распределять на ряд точек симметрично в обе стороны от точки перелома. Такое распределение делается в графе 8 табл. 5. Симметричное распределение общей поправки не изменяет общего направления проектной линии, а лишь заменяет один крутой перелом несколькими пологими переломами.
Графа 9 табл. 5 заполняется данными из графы 3 с учетом распределенных поправок графы 8. Может оказаться, что на одну и туже точку приходятся две, а иногда и три распределенные поправки, например, в точке 12 рассматриваемого примера. В таком случае поправка в расчетную стрелу будет равна алгебраической сумме распределенных поправок для одной и той же точки.
Проектные стрелы (расчетные с поправками) не должны иметь отклонений, нарушающих плавность кривой. Отклонения могут образоваться в результате неудачного распределения общих поправок в расчетные стрелы. Проектные стрелы, имеющие отклонения, должны быть отрегулированы. В стрелу, которая имеет отклонения, вносится основная четная поправка с определенным знаком; в целях сохранения суммы проектных стрел основная поправка компенсируется четным количеством поправок с обратным знаком, которые в сумме должны равняться основной поправке. Компенсирующие поправки распределяются на точки, симметрично расположенные относительно точки с основной поправкой.
В рассматриваемом примере плавность кривой с внесением поправок не нарушается. По данным графы 9 табл. 5 строится график проектных стрел (см. рис. 21).
Заполнение граф 11, 12, 13 табл. 5 производится так же, как и граф 4, 5, 6. В графу 14 вписываются проектные сдвижки, равные удвоенным полусдвигам, т. е. удвоенным данным графы 13.
Имеющиеся приборы для расчета кривых, например приборы И. Я. Туровского, основаны также на подборе проектных стрел исходя из натурных.
Кроме того, в паспорте кривой имеется график проектных стрел; на этот график наносят и графики натурных стрел, вычерчиваемые ежегодно по данным осенней проверки в течение срока действия паспорта (4 года). Анализ этих графиков помогает выявлению неустойчивых мест кривой и причин ее расстройства, позволяет наметить мероприятия по предупреждению и устранению причин расстройства кривой.