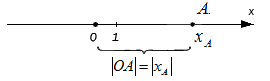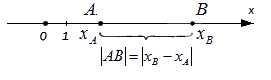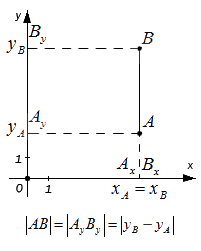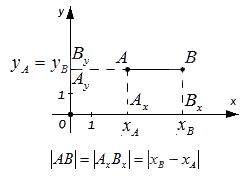как узнать расстояние по координатам
Как вычислить расстояние между координатами gps
Содержание статьи
Что такое координаты GPS
С помощью координат определяют местоположение объекта на земном шаре. Координаты обозначаются в градусах по широте и долготе. Широты отсчитываются от линии экватора по обеим сторонам. В Северном полушарии широты положительные, в Южном полушарии – отрицательные. Долгота отсчитывается от начального меридиана либо на восток, либо на запад, соответственно получается либо восточная долгота, либо западная.
Согласно общепринятому положению, за начальный меридиан принят меридиан, который проходит через старую Гринвичскую обсерваторию в Гринвиче. Географические координаты местоположения можно получить с помощью GPS-навигатора. Этот прибор получает сигналы спутниковой системы позиционирования в системе координат WGS-84, единой для всего мира.
Модели навигаторов различаются по производителям, функционалу и интерфейсу. В настоящее время встроенные GPS-навигаторы имеются и в некоторых моделях сотовых телефонов. Но любая модель может записать и сохранить координаты точки.
Расстояние между координатами GPS
Для решения практических и теоретических задач в некоторых отраслях производства необходимо уметь определять расстояния между точками по их координатам. Для этого можно использовать несколько способов. Каноническая форма представления географических координат: градусы, минуты, секунды.
Следующий способ более трудоемкий, но и более наглядный. Необходимо воспользоваться любой доступной картографической или навигационной программой. К программам, в которых можно создать точки по координатам и измерить расстояния между ними, относятся следующие приложения: BaseCamp (современный аналог программы MapSource), «Google Планета Земля», «SAS.Планета».
Все вышеперечисленные программы доступны для любого пользователя сети. К примеру, для расчета расстояния между двумя координатами в программе «Google Планета Земля» необходимо создать две метки с указанием координат первой точки и второй точки. Затем при помощи инструмента «Линейка» нужно соединить линией первую и вторую метки, программа автоматически выдаст результат промера и покажет путь на спутниковом снимке Земли.
В случае с примером, приведенным выше, программа «Google Планета Земля» выдала результат – протяженность расстояния между точкой №1 и точкой №2 составляет 3 817 353 м.
Расчет расстояний между городами по их координатам
Расчет расстояний между точками по их координатам на плоскости элементарен, на поверхности Земли — немного посложнее: мы рассмотрим измерение расстояния и начального азимута между точками без проекционных преобразований.
Для начала разберемся в терминологии.
Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.
Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Формулы
Существует три способа расчета сферического расстояния большого круга.
1. Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.
φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах
Δλ — разница координат по долготе
Δδ — угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
2. Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
3. Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
Как измерить расстояние на карте с помощью градусной сетки?
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
Как самому подсчитать расстояние в километрах по координатам долготы и широты?
Приходит запрос с клиента с его данными gps(android,ios) и делаю запрос в mysql чтобы выбрать ближайший к нему необходимый мне объект(там хранится как раз объект долгота широта)
То есть от долготы объекта отнимаю по модулю долготу юзере и тоже самое с широтой
и так итераций для каждого из объектов
затем
usort($ArrReadyToSort, «cmp»);
сортирую и беру нулевой элемент, в данном случае по результату сортировки это ближайший, так вот
в итоге самый ближайший это ассоциативный массив с коэфициентом
этого действия
и два других элемента это точки пользователя и точки вот этого ближайшего объекта, нужно либо как то коэфициент перевести в километры( в идеале) либо curl в google api и получить расстояние отдав точки либо на клиент вернуть и с него сделать зарпос в api(что ваще не быстро)
поэтому вопрос в том как имея ближайший объект к пользователю, точки пользователя и объекта и коэфициент выше найти расстояние в км/м/хоть в чем то
SQL запрос для нахождения ближайших точек с отображением дистанции до каждой. Под MySQL.
PHPGeo — простая библиотека для измерения расстояния между двумя координатами с высокой точностью. Она использует формулу Гаверсинуса и Винсента для вычисления расстояния. Вы можете интегрировать ее с любым приложением, связанным с картами или местоположениями.
Доброго времени суток, уважаемые! )
У меня вот похожая задачка, но не могу сообразить как применить данную формулу в MySQL.
Мне нужно по списку координат вычислить общее пройденное расстояние желательно в км, или метрах за заданный отрезок времени..
Кто то может мне помочь сформировать MySQL запрос чтобы эта формула обработала координаты и выдала общее суммарное расстояние?
Далее вызываем эту функцию и делаем суммирование пройденного пути:
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
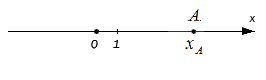
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Расстояние между точками на плоскости
— если точки А и В совпадают, то расстояние между ними равно нулю;
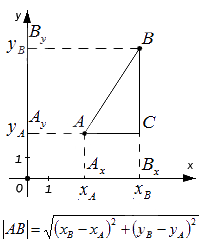
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
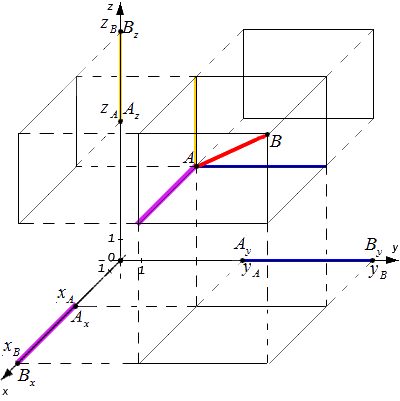
Расстояние между точками в пространстве
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Решение
Решение
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Решение