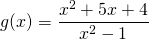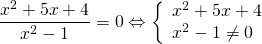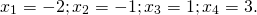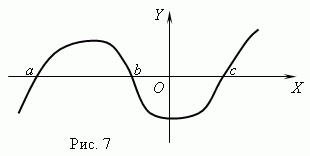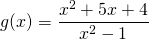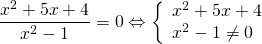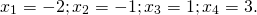как узнать сколько нулей у функции
Нули функции
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
1) Найти нули линейной функции y=3x+15.
Чтобы найти нули функции, решим уравнение 3x+15 =0.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Для нахождения нулей функции решим квадратное уравнение
Его корни x1=3 и x2=4 являются нулями данной функции.
3)Найти нули функции
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Как найти нули функции?
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
График функции у=k/x выглядит следующим образом: 
Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.
Значит, нули функции это числа (-76) и 95.
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Метод интервалов: примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
произведение линейных двучленов с коэффициентом 1 при переменной х;
произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Как найти нули функции по графику. Что такое нули функции и как их определить
Примеры
Рассмотрим другой пример:
Подставим 0 в левую часть уравнения, как и в предыдущем примере:
Алгоритм определения
Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:
Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.
Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.
Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.
Типичные ошибки
Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти «потерянные» сомножители.
Графическое представление
Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.
Является нулём, поскольку
Понятие нулей функции можно рассматривать для любых функций, область значений которых содержит нуль или нулевой элемент соответствующей алгебраической структуры.
Корень многочлена
См. также
Литература
Смотреть что такое «Нуль функции» в других словарях:
Точка, где заданная функция f (z) обращается в нуль; таким образом, Н. ф. f (z) это то же самое, что и корни уравнения f (z) = 0. Например, точки 0, π, π, 2π, 2π. суть нули функции sinz. Нули аналитической функции (См. Аналитические… …
Нуль функция, нуль функции … Орфографический словарь-справочник
У этого термина существуют и другие значения, см. Нуль. Необходимо перенести содержимое этой статьи в статью «Нуль функции». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот … Википедия
Или C строка (от названия языка Си) или ASCIZ строка (от названия директивы ассемблера.asciz) способ представления строк в языках программирования, при котором вместо введения специального строкового типа используется массив символов, а концом… … Википедия
В квантовой теории поля принятое (жаргонное) название для свойства обращения в нуль фактора перенормировки константысвязи где g0 затравочная константа связи из лагранжиана взаимодействия, физ. константа связи, одетая взаимодействием. Равенство Z … Физическая энциклопедия
Утверждение в теории вероятностей о том, что всякое событие (т. н. остаточное событие), наступление к рого определяется лишь сколь угодно удаленными элементами последовательности независимых случайных событий или случайных величин, имеет… … Математическая энциклопедия
1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия
Функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение x2 + y2 1 = 0 задаёт Н. ф. … Большая советская энциклопедия
2. Найдем нули функции.
f(x) при х 
Ответ f(x) при х 
Пусть f(x)=х 2 +4х +5 тогда Найдем такие х при которых f(x)>0,
4. Системы неравенств. Неравенства и системы неравенств с двумя переменными
1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 — как раз наоборот, монотонная, но неограниченная. (Объясните это, пожалуйста!).
2) существует конечный предел lim f (x ) ;
Следовательно, добавление 2 n к аргументу синуса не
sin (/ 2 + P ) = sin / 2 = 1.
из двух последних равенств следует, что cos P = 1, но мы
значение функции. Наименьшее отличное от нуля число
Тема 6. «Метод интервалов».
Свойство непрерывных функций.
Если на интервале (a ; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
На этом свойстве основан метод решения неравенств с одной переменной – метод интервалов. Пусть функция f(x) непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция f(x) c охраняет постоянный знак. Чтобы определить этот знак, достаточно вычислить значение функции f(x) в какой-либо одной точке из каждого такого интервала. Исходя из этого, получим следующий алгоритм решения неравенств методом интервалов.
Метод интервалов для неравенств вида
Метод интервалов. Средний уровень.
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Линейная функция
Линейной называется функция вида. Рассмотрим для примера функцию. Она положительна при 3″> и отрицательна при. Точка – нуль функции (). Покажем знаки этой функции на числовой оси:
Говорим, что «функция меняет знак при переходе через точку ».
Видно, что знаки функции соответствуют положению графика функции: если график выше оси, знак « », если ниже – « ».
Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:
Квадратичная функция
Теперь вспомним, какие знаки принимает квадратичная функция. Ее график – парабола, и функция принимает знак « » при таких, при которых парабола выше оси, и « » – если парабола ниже оси:
Если у функции есть нули (значения, при которых), парабола пересекает ось в двух точках – корнях соответствующего квадратного уравнения. Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.
А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?
Вспомним, что квадратный трехчлен можно разложить на множители:
Отметим корни на оси:
Мы помним, что знак функции может меняться только при переходе через корень. Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.
В нашем примере: при 3″> оба выражения в скобках положительны (подставим, например: 0″>). Ставим на оси знак « »:
Ну и, при (подставь, например,) обе скобки отрицательны, значит, произведение положительно:
Это и есть метод интервалов : зная знаки сомножителей на каждом интервале, определяем знак всего произведения.
Рассмотрим также случаи, когда нулей у функции нет, или он всего один.
Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак. Его легко определить, подставив в функцию.
Если корень только один, парабола касается оси, поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?
Если разложить такую функцию на множители, получатся два одинаковых множителя:
А любое выражение в квадрате неотрицательно! Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:
Метод интервалов в неравенствах
Теперь любое квадратное неравенство можно решать без рисования параболы. Достаточно только расставить на оси знаки квадратичной функции, и выбрать интервалы в зависимости от знака неравенства. Например:
Отмерим корни на оси и расставим знаки:
Нам нужна часть оси со знаком « »; так как неравенство нестрогое, сами корни тоже включаются в решение:
Теперь рассмотрим рациональное неравенство – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).
Все множители кроме одного – – здесь «линейные», то есть, содержат переменную только в первой степени. Такие линейные множители нам и нужны для применения метода интервалов – знак при переходе через их корни меняется. А вот множитель вообще не имеет корней. Это значит, что он всегда положительный (проверь это сам), и поэтому не влияет на знак всего неравенства. Значит, на него можно поделить левую и правую часть неравенства, и таким образом избавиться от него:
Теперь все так же, как было с квадратными неравенствами: определяем, в каких точках каждый из множителей обращается в нуль, отмечаем эти точки на оси и расставляем знаки. Обращаю внимание очень важный факт:
В случае четного количества поступаем так же, как и раньше: обводим точку квадратиком и не меняем знак при переходе через корень. А вот в случае нечетного количества это правило не выполняется: знак все-равно поменяется при переходе через корень. Поэтому с таким корнем ничего дополнительно не делаем, как будто он у нас не кратный. Вышеописанные правила относятся ко всем четным и нечетным степеням.
Что запишем в ответе?
Как определить нули функции по графику
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
1) Найти нули линейной функции y=3x+15.
Чтобы найти нули функции, решим уравнение 3x+15 =0.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Для нахождения нулей функции решим квадратное уравнение
Его корни x1=3 и x2=4 являются нулями данной функции.
3)Найти нули функции
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0, x² ≠ 1,x ≠±1. То есть область определения данной функции (ОДЗ)
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
Это можно сделать и графически. Просто построить функцию по точкам и начертить, точки пересечения графика с осью Х и будут нулями функции.
Посмотрите еще здесь:
2.Ну просто f(x)=0
Приравниваем функцию к нулю и считаем «нули» 🙂
Ответ или решение 1
Решение: Точки пересечения графика с осью абсцисс, на которой откладываются аргументы х, называются нулями функции. Поиск возможных нулей – одна из задач по исследованию заданной функции. Другими словами, нуль функции – что такое значение аргумента х, при котором значение функции равно нулю. Однако нулями могут быть лишь те аргументы, которые входят в область определения исследуемой функции. То есть в такое множество значений, для которых функция f(x) имеет смысл.
С осью абсцисс она пересекается один раз в точке (92;0).