как узнать скорость движения автомобиля
Как определить скорость движения
Чтобы определить скорость равномерного движения нужно разделить длину пройденного пути на время, которое потребовалось на этот путь:
v=s/t, где:
v – это скорость,
s – длина пройденного пути, а
Определите максимальную скорость автомобиля.
Решение.
Так как после разгона автомобиль двигался на максимальной скорости, то ее по условиям задачи можно считать равномерной. Следовательно:
s=1 км,
t=0,5 мин.
Приводим единицы измерения времени и пройденного пути к одной системе (СИ):
1 км=1000 м
0,5 мин= 30 сек
Значит, максимальная скорость автомобиля:
1000/30=100/3=33 1/3 м/с, или приблизительно: 33,33 м/с
Ответ: максимальная скорость автомобиля: 33,33 м/с.
Для определения скорости тела при равноускоренном движении необходимо знать начальную скорость и величину ускорения или другие связанные параметры. Ускорение может быть и отрицательным (в этом случае это, фактически, торможение).
Скорость равна начальной скорости плюс ускорение, умноженное на время. В виде формулы это записывается следующим образом:
v(t)= v(0)+аt, где:
v(t) – скорость тела в момент времени t
v(0) – начальная скорость тела
а – величина ускорения
t – время, прошедшее с момента начала ускорения
Примечание.
1. Подразумевается движение по прямой линии.
2. Начальная скорость, так же как и ускорение, может быть отрицательной относительно выбранного направления.
3. Ускорение свободного падения обычно принимается равным 9,8 м/с²
Пример 2
С крыши вниз кинули кирпич со скоростью 1м/с. Через 10 секунд он долетел до земли.
Чему была равна скорость кирпича в момент приземления?
Решение.
Так как направление начальной скорости и ускорения свободного падения совпадают, то скорость кирпича у поверхности земли будет равной:
1+9,8*10=99 м/с.
Сопротивление воздуха в задачах такого рода, как правило, не учитывается.
Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Время, скорость, расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи
Немного из школьного курса математики и геометрии — как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи.
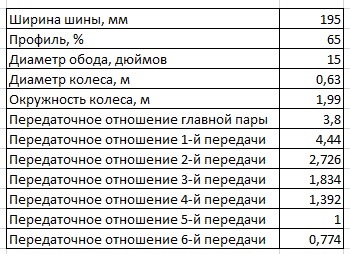
Для этого необходимо знать размерность шин и передаточные отношения главной пары и передач в коробке передач…
Формулы:
Диаметр колеса: Ширина шины, м х Профиль, % х 2 + Диаметр обода, дюймов х 2,54/100
Пример: шина 195/65R15: 0,195 х 0,65 х 2 + 15 х (2,54 / 100) = 0,63 м
Используя формулу диаметра колеса, можно посчитать на сколько изменится клиренс, поделив изменение диаметра на 2
Окружность колеса: Диаметр колеса х число Пи (3,14)
Пример: 0,63 м х 3,14 = 1,98 м
Используя формулу окружности колеса, можно посчитать на сколько процентов изменятся показания одометра и спидометра при замене дисков и/или резины, поделив новое значение окружности на старое и отняв единицу, и умножив полученное значение на сто
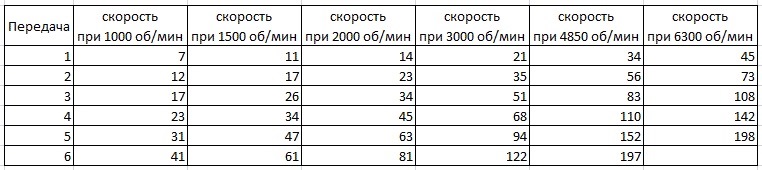
Скорость автомобиля при 1 000 об/мин на выбранной передаче: Окружность колеса делим на произведение передаточного отношения главной пары и передаточного отношения выбранной передачи, полученное число умножаем на 60 (минут в часе) и делим на 1 000 (метров в километре), далее полученное число умножаем на число оборотов двигателя в минуту (в нашем случае 1 000 об/мин)
Пример: [1,98 / (3,8 х 1 (пятая передача))] х (60 / 1 000) х 1 000 = 31 км/ч
Технические данные для расчетов (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
Непосредственно сами расчеты (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
* Максимальная мощность на этом двигателе достигается при 6 300 об/мин, максимальный крутящий момент — при 4 850 об/мин
Три способа определить скорость автомобиля при ДТП
После каждого дорожно-транспортного происшествия обязательно определяется скорость транспортного средства до и в момент удара или наезда. Данная величина имеет столь большое значение по нескольким причинам:
Определение скорости автомобиля по тормозному пути
Под тормозным путём обычно понимают расстояние, которое проходит то или иное транспортное средство от начала торможения (или, если быть более точным, с момента активации тормозной системы) и до полной остановки. Общая, недетализированная формула, из которой возможно вывести формулу для расчета скорости, выглядит так:
Va = 0.5 х t3 х j + √2Sю х j = 0,5 0,3 5 + √2 х 21 х 5 = 0,75 +14,49 = 15,24м/с = 54,9 км/ч где: в выражении √2Sю х j, где:
Исходя из указанного выше уравнения, можно сделать вывод, что на тормозной путь влияет в первую очередь скорость автомобиля, которую при известных остальных величинах нетрудно вычислить. Наиболее сложной частью вычислений по этой формуле является точное определение коэффициента трения, так как на его значение влияет целый ряд факторов:
Для точного результата расчётов также нужно принимать во внимание особенности тормозной системы конкретного транспортного средства, например:
Тормозной след
После достаточно быстрой активации тормозной системы на дорожном покрытии остаются отпечатки – тормозные следы. В случае если колесо во время торможения заблокировано полностью и не вращается, остаются сплошные следы, (которые иногда называют «след юза») которые многие авторы призывают считать следствием максимально возможного нажатия на педаль тормоза («тормоз в пол»). В случае же когда педаль нажата не до конца (или присутствует какой-либо дефект тормозной системы) на дорожном покрытии остаются как бы «смазанные» отпечатки протектора, которые образуются вследствие неполной блокировки колес, которые при таком торможении сохраняют возможность вращаться.
Остановочный путь
Остановочным путём считают то расстояние, которое проходит определённое транспортное средство начиная с обнаружения водителем угрозы и до остановки автомобиля. Именно в этом заключается главное отличие тормозного пути и остановочного пути – последний включает в себя и расстояние, которое преодолел автомобиль за время срабатывания тормозной системы, и расстояние, которое было преодолено за время, понадобившееся водителю на осознание опасности и реакции на нее. На время реакции водителя влияют такие факторы:
Определение скорости исходя из закона сохранения количества движения
Возможно также и определение скорости движения автомобиля по характеру его перемещения после столкновения, а также, в случае столкновения с другим транспортным средством, по перемещению второй машины в результате передачи кинетической энергии от первой. Особенно часто данный метод используют при столкновениях с неподвижными транспортными средствами, или если столкновение случилось под углом, близким к прямому.
Определение скорости автомобиля исходя из полученных деформаций

Это связано с огромным количеством факторов, влияющих на образование повреждений, а также с тем, что некоторые факторы попросту невозможно учесть. Оказывать влияние на образование деформаций могут:
Определение скорости в момент наезда (столкновения)
Скорость в момент наезда обычно определяют по тормозному следу, но если это по ряду причин не представляется возможным, то приблизительные цифры скорости можно получить анализируя травмы, полученные пешеходом, и повреждения, образовавшиеся после наезда на транспортном средстве.
К примеру, о скорости автомобиля можно судить по особенностям бампер-перелома – специфической для наезда автомобилем травмы, которая характеризуется наличием поперечно-осколочного перелома с крупным отломком кости неправильной ромбообразной формы на стороне удара. Локализация при ударе бампером легкового автомобиля – верхняя или средняя треть голени, для грузового автомобиля – в участке бедра.
Анализ методов определения скорости автомобиля при ДТП
По тормозному следу
Достоинства:
Недостатки:
По закону сохранения количества движения
Преимущества:
Недостатки:
Исходя из полученных демормаций
Преимущества:
Недостатки:
На практике чаще всего используют два метода – определение скорости по следу торможения и исходя из закона сохранения количества движения. При использовании двух этих методов одновременно обеспечивается максимально точный результат, так как методики дополняют друг друга.
Остальные способы определения скорости транспортного средства значительного распространения не получили по причине недостоверности получаемых результатов и/или необходимости громоздких и сложных вычислений. Также при оценке скорости автомобиля учитывают показания свидетелей происшествия, хотя в таком случае нужно помнить о субъективности восприятия скорости разными людьми.
В некоторой мере помочь разобраться с обстоятельствами происшествия и в итоге получить более точный результат может помочь анализ видео из камер наблюдения и видеорегистраторов.