как узнать вершину прямоугольника
Прямоугольник
Прямоугольник — это выпуклый многоугольник. Прямоугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
В тексте прямоугольники обозначаются четырьмя прописными латинскими буквами, стоящими при вершинах — ABCD.
У прямоугольников противоположные стороны параллельны и равны:
В прямоугольнике ABCD точки A, B, C и D — это вершины прямоугольника, отрезки AB, BC, CD и DA — стороны. Углы, образованные сторонами, называются внутренними углами или просто углами прямоугольника.
Главное отличие прямоугольников от остальных четырёхугольников — четыре прямых внутренних угла:
Свойства диагоналей
Отрезки, соединяющие противолежащие вершины прямоугольника, называются диагоналями.
Отрезки AC и BD — диагонали, O — точка пересечения диагоналей.
В любом прямоугольнике можно провести всего две диагонали. Они обладают следующими свойствами:
Квадрат — прямоугольник, у которого все стороны равны. Диагонали квадрата обладают всеми свойствами диагоналей прямоугольника. Также диагонали квадрата имеют и дополнительных свойства:
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
Из равенства (1) найдем d:
Пример 1. Стороны прямоугольника равны 
. Найти диагональ прямоугольника.
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:
 |
Ответ: 
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
Подставляя (3) в (2), получим:
Пример 2. Стороны прямоугольника равны 
. Найти радиус окружности, описанной вокруг прямоугольника.
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:
 |
 |
Ответ: 
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
где \( \small a \) и \( \small b \) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:
 |
Ответ: 
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем \( \small b \) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):
Вычислим дискриминант квадратного уравнения (10):
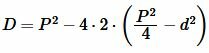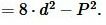  | (11) |
Сторона прямоугольника вычисляется из следующих формул:
После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
Пример 4. Диагональ прямоугольника равна 
, а периметр равен 
. Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):
 |
Подставляя значения и 
в первую формулу (12), получим:
 |
Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и 
в формулу, получим:
 |
Ответ: 
, 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
Форумы CADUser → Программирование → VBA → Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Сообщения 12
#1 Тема от SmeL 1 ноября 2005г. 12:36:43
Тема: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
хочу рисовать прямоугольник при помощи мауса по дум точкам (диогональ), и через угол показывать линию, на которой лежит одно ребро. Вот только не помню геометрию как, просчитать еще две вершины 😉 может кто подкинет код 🙂
#2 Ответ от JS 1 ноября 2005г. 18:28:16
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
#3 Ответ от SmeL 1 ноября 2005г. 19:00:30
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
Спасибо, в данном вводятся те данные которыми я не обладаю. Я придумал другой ввод прямоугольника. Я не ввожу угол вообще т.к. у меня прямоугольник т.е. 90. Исходные данные диагональ, и угол который нужен для того чтоб показать, что на нем именно лежит одна из сторон.
А вот как построить прямоугольник. диагональ это диаметр окружности, угол это косательная, ее пересечение с окружностью и соединение с другой стороной диаметра и дает угол 90градусов, а для того чтоб найти вторую вершину есть еще несколько вариантов. Осталось настрочить 🙂 вот не знаю как узнать координату пересечения. окружности с косательной.
р.s. колизия насчет того, что все равно 90градусов не получится т.к. окружность это набор прямых. не особо важна.
#4 Ответ от Shogun 1 ноября 2005г. 20:03:14
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
> SmeL
В Cad 2006 команда rectangle уже делает всё что нужно.
Ну а если не устраивает,
то Пифагор Вам поможет: угол известен, гипотенуза тоже.
#5 Ответ от SmeL 1 ноября 2005г. 21:13:12
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
#6 Ответ от SmeL 1 ноября 2005г. 21:21:32
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
#7 Ответ от Shogun 2 ноября 2005г. 12:35:30
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
> SmeL
По моему легче чем построение прямоугольника (при условии что дана диагональ) через правильный треугольник ещё никто не придумал.
Как бы там не было, для построения прямоугольника нужны как минимум две велечины:
диагональ и угол или диагональ и одна из сторон.
Вы же пишете «Я не ввожу угол вообще т.к. у меня прямоугольник т.е. 90» и тут же «Исходные данные диагональ, и угол который нужен для того чтоб показать, что на нем именно лежит одна из сторон.»
И ещё, касательная не может пересекать окружность, на то она и касательная. И если касательная проходит через одну из конечных точек диагонали, тогда она перпендикулярна этой диагонале.
Надеюсь я Вас ничем не обидел. Просто не совсем понятно какие данные Вы собираетесь вводить для построения фигуры. Ваши действия по пунктам, если можно.
P.S. Вариант JS-а очень неплох.
#8 Ответ от SmeL 2 ноября 2005г. 13:14:50
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
> Shogun
Все делаю маусом!
1. два клика (запоминаем координаты) они являются противоположными вершинами нашего прямоуголиника.
2. на основе второй координаты делаем вот что
retAngle = ThisDrawing.Utility.GetAngle(Pnt2).
все все данные для построения прямоугольника введены.
___________
Теперь начинается геометрия.
данные действия проделывает уже VBA
1. На основе двух координат (введенных выше) чертим окружность, таким образом чтоб они образовали диаметр.
2. На основе угла ведем прямую от Pnt2, которая пересекет нашу окружность. (Ваша заметка, что касательная не пересекает окружность принимается но точка соприкосновения существует 😉 я так написал чтоб проще было объяснить)
3. Узнаем координату пересечения окружности и построенной прямой. Теперь у нас есть три вершины, которые образуют прямоугольный трейгольник!
4. Для того как найти четвертую вершину есть несколько вариантов.
___________
Вот весь алгоритм 😉
Вариант JS не плох но у меня другие данные вводятся.
#9 Ответ от Shogun 2 ноября 2005г. 17:33:10
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
> SmeL
По пунктам:
1. Вы фиксируете положение прямоугольника «двумя кликами», т.е вращять прямоугольник после этого не собираетесь.
Верно?
2. Получили угол, без вопросов.
Геометрия:
1. Без вопросов.
2. Прямые, также как полилинии, лучи и Х-линии строятся по точкам, а не по углу. Но не в этом суть, применим PolarPoint(Point, Angle, Distance) и найдем Pnt3 нужную для построения прямой, а ещё лучше луча который должен будет пересечь окружность. Только вот никакого пересечения может и не быть!
Для наглядности округлимся до 1-ого градуса.
Так вот:
1. Если угол между диагональю и лучом в пределах 1-89 градусов, то пересечение состоится.
2. При угле в 0 или 90, Ваша диагональ становится одной из сторон.
3. Угл свыше 90 делает пересечение невозможным.
> SmeL
Не помню себя в 7-ом классе, но даже визуально (логически) формула подходит для определения точек из центра окружности, а не из точки касательной.
#10 Ответ от SmeL 2 ноября 2005г. 18:39:22
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
Вы фиксируете положение прямоугольника «двумя кликами», т.е вращять прямоугольник после этого не собираетесь.
Нет, но было бы не плохо до 3 клика перересовывать прямоугольник, т.е пока двигается маус меняются длины сторон, но это пока только в мечтах.
Крнечно стоящее описание колизии на счет угла равному 0 or 90, но не сомневайтесь я это учел бы и так.
. но даже визуально (логически) формула подходит для определения точек из центра окружности, а не из точки касательной.
Пока только такие формулы, т.е. я думаю пересчитать данные таким образом, чтоб привести задачу к данному виду 🙂 Может кто то имеет формулы по лучше не стесняйтесь поделитесь.
#11 Ответ от Boxa 2 ноября 2005г. 23:32:04
Re: Как найти координаты вершин прямоугольника по координатам его диагонали и углу?
Я может и не оригинален но, по-моему, надо открыть любой вузовский учебник математики и посмотреть раздел «Аналитическая геометрия» и по формулам все решать, без всяких построений
1 По имеющемуся углу и точке находите уравнение одной из сторон
в общем виде выглядит это уравнение так
У=КнХ+Ув
где Кн=tg(угла),
Ув-координата У той точки от которой откладывался угол(здесь от точки В)
2 По имеющемуся уравнению и точке(А) нахожу уравнение прямой перпендикулярной заданной и проходящей через заданную точку
в общем виде это уравнение выглядит так
У-Уа=(-1/Кн)*(Х-Ха)
3 имея 2 уравнения решаю их через систему и получаю точку пересечения сторон прямоугольника, т.е. получаю 3 вершину.
4 нахожу уравнение прямой проходящей через точку В и параллельной найденной в п.3
У-Ув=(-1/Кн)*(Х-Хв)
5 нахожу уравнение прямой параллельной найденной в п.2 и проходящей через точку А
У-Уа=Кн(Х-Ха)
6 Решая систему из уравнений пунктов 5 и 6 получаю координаты еще одной вершины
вот собственно и все. Опускаю все выкладки и причесывания. Привел только теорию.
Все преобразования в уравнениях на уровне 5 класса
Нахождение 4-й вершины прямоугольника
Мне нужен мой код, чтобы найти 4-ую вершину прямоугольника. Пытался что-то сделать но как всегда не получилось. Это работает в некоторых случаях, бот не каждый раз. Может ли кто-нибудь помочь мне с этим?
Кроме того, это должно быть сделано с 2 классами, один для вершин и другой для целого прямоугольника.
Проблема в том, что мой код работает для определенной настройки вершины. Я много чего пробовал, но все равно не получилось.
Поскольку я думаю об этом сейчас, он может иметь какое-то отношение к вставке координат в правильные переменные, но не может придумать решение, чтобы это исправить.
Например:
Входные данные:
1 1
0 3
3 2
Выход:
2 4
Порядок ввода каждой вершины не указан.
Решение
Если у вас есть три вершины, то у вас есть половина прямоугольника: прямоугольный треугольник. Сначала нужно определить, какая точка находится под прямым углом. Вы можете сделать это по-разному. Один из способов — применить теорему Пифагора: найти две самые дальние вершины. Оставшаяся вершина находится под прямым углом (другим способом может быть вычисление скалярного произведения между каждой парой ребер, а та, которая ближе всего к нулю, образует прямой угол).
Другие решения
Работа с векторами — очень интересная тема. Вот несколько хороших объяснений о вектор
Чтобы ответить на ваш вопрос:
Чтобы определить, что прямой угол равен B: произведение точек двух векторов BA и BC равно 0, независимо от порядка A и C.
В C ++ (не C) вы должны добавить операторы для управления векторами в вашем классе вершин, вот пример:
Точечное произведение двух векторов:
Чтобы проверить, находится ли прямой угол в точке B, мы можем использовать следующую функцию, она вычислит произведение точек двух нормализованных векторов AB и BC:
Обратите внимание, что когда мы сравниваем двойное значение с нулем, всегда используем эпсилон, для двойного нет абсолютного нуля. Эта функция также возвращает false, если один из нормализованных векторов не может быть вычислен (две точки расположены слишком близко друг к другу).
Вычислить последнюю координату под прямым углом:
Эта следующая функция возвращает true, если последний кординат D рассчитывается по прямому углу B:
Ищите правильный угол:
Таким образом, чтобы найти последнюю координату D из 3 вершин A, B и C, вы должны выполнить тест для трех случаев прямого угла, тест останавливается, когда решение найдено:
Быстрый тест :
Мы можем сделать быстрый тест, если он работает:
EPSILON CHOICE:
Это зависит от вашего домена: если вы работаете в очень маленьком объектном домене, который (X, Y) очень мал (например, близок к 10E-5), у вас будут некоторые трудности в вычислениях (плавающая точка в GPU очень ограничена в точность). Лучше преобразовать рабочий домен в нормальный диапазон.
В приведенном выше примере EPSILON установлен на 10E-6. Если длина между двумя точками меньше этого значения, эти две точки можно рассматривать как уникальную точку — они остаются в одной и той же позиции).
Найти координаты двух вершин прямоугольника
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Найти координаты вершин вращающегося в описанной окружности прямоугольника
Даны начальные координаты вершин прямоугольника. Его поворачивают на известный угол A внутри.
Найти координаты двух угловых точек прямоугольника не симметричного осям координат
Даны координаты двух нижних угловых точек прямоугольника повернутого на угол alpha (А(x;y) B(x;y)).
Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенные из вершин А
Даны координаты вершин треугольника АВС. Найти длины медианы, высоты, биссектрисы, проведенные из.
Даны, однако, G и H, определить надо F и I.
Теперь найдем точки пересечения соответствующих сторон и получим B и D.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Найти радиус и координаты центра вписанной в тетраэдр сферы, если известны координаты вершин тетраэдра
Хотелось бы узнать как решить эту задачу. Предполагаемое решение:
Даны координаты двух вершин треугольника и точка пересечения его высот
2. 4. Даны координаты двух вершин треугольника А(А1, А2) и В(В1, В2), и точка пересечения его высот.
Найти координаты вершин квадрата, если известны координаты одной вершины и уравнение одной стороны
Найти координаты вершин квадрата, если известны координаты одной вершины (11;23) и уравнение одной.
Найти координаты углов прямоугольника
Как найти координаты углов прямоугольника, если ширина равна W, высота H, угол наклона A градусов.