В чем выражается размерность относительной погрешности вольтметра
Погрешности измерений
Общие сведения об измерениях. Погрешности измерений и средств измерений
Общие сведения об измерениях
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.
Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.
Погрешности измерений
Погрешность является одной из основных характеристик средств измерений.
Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.
Абсолютная погрешность Δa прибора есть разность между показанием прибора ах и истинным значением а измеряемой величины, т.е.
Абсолютная погрешность, взятая с обратным знаком, называется поправкой.
Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна
Приведенная погрешность γП есть выраженное в процентах отношение абсолютной погрешности Δa к нормирующему значению апр
Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).
Погрешности средств измерений
Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Класс точности прибора (например, амперметра) дается выражением
При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.
По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:
В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:
(α = 0) 1; 1,5; 2; 2,5; 4; 5; 6;
(α = 1) 10; 15; 20; 25; 40; 50; 60.
Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.
Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.
Примеры решения задач
Задача №1
Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.
Решение
Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)
постоянна и равна классу точности прибора.
Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)
уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.
Абсолютная погрешность однократного измерения
постоянна на всех отметках рабочей части шкалы прибора.
По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра.
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
 Манометр – прибор для измерения давления, круговая шкала |  Вольтметр – прибор для измерения напряжения, дуговая шкала |  Индикатор громкости звука, линейная шкала |
п.2. Цена деления
Пример определения цены деления:
 | Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. |
Цена деления: \begin Физическую величину измеряют с помощью прибора Измерение длины бруска линейкой Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений Определение площади столешницы при измеренной длине и ширине Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.) Определяется несовершенством методов и допущениями в методике. Погрешность теории (модели) Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности. Определяется субъективным фактором, ошибками экспериментатора. Примеры значащих цифр: В простейших измерениях инструментальная погрешность прибора является основной. Пример получения результатов прямых измерений с помощью линейки: Второе измерение точнее, т.к. его относительная погрешность меньше. Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки). Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений. Пример расчета истинного значения и погрешности для серии прямых измерений: Составим расчетную таблицу: Сначала находим среднее значение всех измерений: \begin Как найти результат прямого измерения, мы рассмотрели выше. Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса. Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? Составим таблицу для расчета цены деления: Инструментальная точность мензурки равна половине цены деления. Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке. Ответ: Мерой точности является относительная погрешность измерений. Получаем: \begin Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч. Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины. Методы нормирования погрешности. Класс точности средств измерений Различные средства измерения обладают погрешностями, характер проявления которых может быть различным: у одних погрешность аддитивная, у других мультипликативная или нелинейная, а у третьих могут сочетаться все указанные погрешности. Кроме того, у каждого средства измерения могут наблюдаться случайные и систематические погрешности. Для того чтобы ориентироваться в метрологических свойствах конкретного средства измерения пользуются так называемыми нормированными значениями погрешности. Под нормированным значением погрешности понимается погрешность, являющаяся предельной для данного типа средства измерения Класс точности – это обобщенная метрологическая характеристика СИ, определяемая пределами основной и дополнительной погрешностей. Классы точности условными обозначениями наносятся на циферблаты, щитки, корпуса средства измерения. Номинальным условиям работы прибора соответствует установка прибора в положение, указанное на его шкале, нормальная температура окружающей среды (+20° С), отсутствие внешнего электромагнитного поля (кроме земного). Номинальной величиной прибора называется верхний предел измерения его. Заменив в (8-2) Δx ее выражением из (8-1) Следовательно, погрешность измерения равна погрешности прибора, умноженной на отношение номинальной величины прибора к найденному значению измеренной величины. Примеры решения задач Задача №1 Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора. Решение 1. Класс точности указывают просто числом предпочтительного рода, например, 0,5. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой. Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению) постоянна и равна классу точности прибора. Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины) уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора. Абсолютная погрешность однократного измерения постоянна на всех отметках рабочей части шкалы прибора. По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра. 2. Приведенная погрешность 3. Наибольшая абсолютная погрешность вольтметра 4. Относительная погрешность вольтметра для точек Задача №2 При измерении напряжения двумя параллельно включенными вольтметрами их показания были: U1 = 29,2 В, U2 = 30 В. Показания какого прибора точнее, если класс точности КV1 = 2,5, КV2 = 1,0, а пределы измерения соответственно равны Uпр1 = 30 В; Uпр2 = 150 В. Решение Класс точности указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Тогда абсолютные погрешности измерения напряжения вольтметрами Более точным будет первый вольтметр. Задача №3 Ток 159 мА измеряется цифровым вольтметром с трехразрядным цифровым индикатором и амперметром с классом точности 0,5 и пределом шкалы 250 мА. Каким прибором ток будет измерен точнее? Решение Абсолютная погрешность однократного измерения амперметром где Iпр – измеренное значение электрической величины; К – класс точности прибора. Относительная погрешность однократного измерения амперметром где Iизм – предел шкалы амперметра. В задаче наряду с аналоговым измерительным прибором используется цифровой. Абсолютная погрешность ΔI цифрового прибора принимается равной единице младшего разряда числа, высвечиваемого на цифровом индикаторе. Класс точности аналогового амперметра пределом шкалы Iпр = 250 мА выражается одним числом К = 0,5. Оценка погрешности однократного измерения аналогового амперметра Ток Iизм = 159 мА измеряется цифровым вольтметром с трехразрядным цифровым индикатором. Абсолютную погрешность ΔI цифрового прибора принимается равной единице младшего разряда числа, высвечиваемого на цифровом индикаторе: ΔI = 1 мА. Откуда, абсолютная погрешность цифрового амперметра меньше чем аналогового. Следовательно, цифровой вольтметр точнее измеряет ток Iизм = 159 мА. Задача №4 Значения класса точности аналогового вольтметра К = 0,5. Какой будет относительная и абсолютная погрешности однократных измерений напряжения Uизм = 1; 3; 9 В на пределе измерения Uпр = 10 В? Решение Класс точности прибора выражается одним числом К. Предельная погрешность где ΔA – абсолютная погрешность, Aпр – предел шкалы измерительного прибора. Для оценки погрешности однократного измерения полагаем абсолютную погрешность Относительная погрешность однократного измерения где Aизм – измеренное значение электрической величины. Класс точности аналогового вольтметра с пределом шкалы Uпр = 10 В при измерении постоянного напряжения выражается одним числом К = 0,5. Относительная погрешность однократных измерений напряжения Uизм = 1; 3; 9 В: Абсолютная погрешность однократных измерений напряжения Uизм = 1; 3; 9 В: Запишем результаты измерений напряжений Uизм =1; 3; 9 В: Контрольно-оценочные средства включают в себя выполнение практической работы, в которую входят 3 задания. Каждое задание содержит 5 вариантов. Задания 1–решение задачи согласно своему варианту Задания 2–решение задачи согласно своему варианту Задания 3–решение задачи согласно своему варианту По итогу оценивания практической работы– бальное с переводом в традиционную пятибалльную. максимальное количество баллов – 15 3 задания – оценка «5»; 2 задания – оценка «4»; 1 задание – оценка «3»; При выставлении экзаменационной оценки по дисциплине ОП.1 Электротехника в экзаменационную ведомость (протокол) выставляется оценка, рассчитанная по формуле: 𝑛т.у. – средняя оценка текущей аудиторной успеваемости; Государственное образовательное учреждение высшего профессионального образования «Омский государственный технический университет» Рефератп.3. Виды измерений
п.4. Погрешность измерений, абсолютная и относительная погрешность
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:п.5. Абсолютная погрешность серии измерений
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.№ опыта 1 2 3 Сумма Масса, г 99,8 101,2 100,3 301,3 Абсолютное отклонение, г 0,6 0,8 0,1 1,5
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin
Поэтому абсолютная погрешность измерения массы: \begin п.6. Представление результатов эксперимента
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.п.7. Задачи
№ мензурки a, мл b, мл n \(\triangle=\frac 1 20 40 4 \(\frac<40-20><4+1>=4\) 2 100 200 4 \(\frac<200-100><4+1>=20\) 3 15 30 4 \(\frac<30-15><4+1>=3\) 4 200 400 4 \(\frac<400-200><4+1>=40\)
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):№ мензурки Объем \(V_0\), мл Абсолютная погрешность
\(\triangle V=\frac<\triangle><2>\), млОтносительная погрешность
\(\delta_V=\frac<\triangle V>1 68 2 3,0% 2 280 10 3,6% 3 27 1,5 5,6% 4 480 20 4,2%
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.Электрические измерения, погрешности электрических измерений
Относительная погрешность измерения величины x1 может быть определена как отношение наибольшей возможной абсолютной погрешности прибора Δx к измеренному значению величины x1 т. е.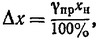
Погрешность при измерении какой-либо величины данным прибором тем меньше, чем ближе измеряемая величина к номинальной величине прибора: следовательно, для лучшего использования точности прибора им следует измерять величины, значения которых соответствуют второй половине шкалы прибора.
Погрешности прибора и измерения могут быть как положительными, так и отрицательными.Uизм = Ui, В 5 10 15 20 25 30 δU, % 3,0 1,5 1,0 0,75 0,6 0,5 Погрешность цифровых вольтметров
Кафедра «Автоматизированные системы обработки информации и управления»
на тему «Погрешность цифровых вольтметров»
по дисциплине «Метрология»
студента
Пояснительная записка
Зав.кафедрой, дтн, проф.
Студент
 Погрешность цифровых вольтметров
Погрешность цифровых вольтметров
Стремительное шествие цифровых технологий привело к интенсивному повсеместному использованию приборов с цифровой формой представления результатов измерений. Цифровые вольтметры прочно вошли в метрологию, что стало следствием таких их достоинств, как высокая точность и разрешающая способность, широкий диапазон измерений, представление результатов измерений в цифровой форме (сводящей до минимума глазомерные ошибки и создающие удобство считывания показаний прибора на расстоянии), возможность получения результатов наблюдений в форме, удобной для ввода в компьютер, и возможность включения их в состав измерительно-вычислительных комплексов.
Наиболее широко используемым в практике классом цифровых вольтметров являются приборы, позволяющие проводить измерения с точностью в пределах 0,05–0,1 %.
Классификации погрешностей измерений:
1) по форме выражения погрешности подразделяют на абсолютные и относительные. Погрешность, выраженная в единицах измеряемой величины, называется абсолютной. Если измеренная величина превышает действительное значение, погрешность положительна, если же действительное значение больше измеренного – отрицательна. Абсолютная погрешность характеризует качество измерений только однородных величин примерно одинакового размера.
Относительной погрешностью называется отношение абсолютной погрешности к истинному значению измеряемой величины: δQ=ΔQ/Qиcт ≈ ΔQ/Qд. Как правило, относительные погрешности выражают в процентах. Относительная погрешность может характеризовать качество измерений, как разнородных величин, так и однородных величин разного размера. Для оценки качества измерения необходимо вычислить относительные погрешности: меньшая погрешность при прочих равных условиях характеризует более высокое качество измерений.
В метрологии пользуются понятием точность измерений, причем точность – величина, обратная относительной погрешности.
2) по причине возникновения погрешности разделяют на две группы: объективные погрешности, не связанные с человеком-оператором, производящим измерения, и субъективные (личные), обусловленные экспериментатором, состоянием его органов чувств, опытом и т.д. В свою очередь, объективные погрешности разделяются на погрешности опознания объекта, методические, инструментальные погрешности и погрешности, обусловленные внешними условиями.
Погрешности опознания объекта измерения связаны с несоответствием реального объекта принятой модели.
Погрешности метода обусловлены несовершенством метода измерений, упрощающими предположениями, принятыми при обосновании метода. К этим погрешностям относятся составляющие погрешности, вызываемые влиянием средства измерения на измеряемую цепь.
Инструментальные погрешности возникают из-за несовершенства средств измерения, их схем, конструкций, состояния в процессе эксплуатации. Каждое средство измерения характеризуется свойственной ему погрешностью, которая входит в общую погрешность измерения.
3) по закономерностям проявления погрешностей различают систематические, случайные, грубые погрешности измерений и промахи.
Систематическая погрешность Δc – это составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в одних и тех же условиях. Закономерно изменяющаяся систематическая погрешность, в свою очередь, может быть прогрессирующей (возрастающей, убывающей), периодической или изменяющейся по сложному непериодическому закону. К постоянным систематическим погрешностям относят, например, погрешность градуировки шкалы, погрешность значения меры, температурную погрешность. К переменным систематическим погрешностям относят погрешности, обусловленные изменением напряжения питания (разряд аккумуляторной батареи), погрешности, связанные с действием электромагнитных помех и т.д.
Систематические погрешности могут быть обнаружены и оценены. Если систематическая погрешность достаточно точно определена, она может быть исключена введением поправки или поправочного множителя.
Поправка – значение величины, одноименной с измеряемой, прибавляемое к измеренной величине для исключения систематической погрешности. Поправка равна абсолютной систематической погрешности, взятой с обратным знаком.
Поправочный множитель – число, на которое умножают результат измерения с целью исключения систематической погрешности.
Случайная погрешность Δсл – составляющая погрешности измерения, которая при повторных измерениях в одних и тех же условиях изменяется случайным образом, т.е. без видимой закономерности. Случайные погрешности являются следствием случайных процессов, протекающих в измерительных цепях. Для оценки погрешностей и разработки способов уменьшения их влияния на результат измерения используют аппарат теории вероятностей и математической статистики. По мере того, как будут изучены отдельные процессы из множества, установлены их закономерности, погрешности из случайных перейдут в категорию систематических.
Таким образом, результат измерения всегда содержит как систематическую, так и случайную погрешности: Δ=Δс+Δсл.
Грубой погрешностью называют погрешность, существенно превышающую погрешность, оправданную условиями измерения, свойствами примененных средств измерений, методом измерения, квалификацией экспериментатора. Грубые погрешности могут появляться вследствие резкого изменения влияющей величины на результат измерения. Грубые погрешности обнаруживают статистическими методами и исключают из рассмотрения.
Промахи являются следствием неправильных действий экспериментатора. Это может быть описка при записи результатов, неправильно снятые показания прибора и т.д. Промахи обнаруживают нестатистическими методами, их следует всегда исключать из рассмотрения.
Также погрешности разделяют на: статические и динамические. Статические погрешности имеют место при статических измерениях, т.е. при неизменной во времени измеряемой величине, динамические – при динамических измерениях, т.е. при переменной во времени измеряемой величине. Динамическая погрешность возникает вследствие инерционности свойств средств измерений. Для оценки динамической погрешности необходимо знать передаточную функцию средства измерения, а также характер изменения измеряемой величины.
Пример
Выбираем цифровой вольтметр для измерения напряжения постоянного тока (рисунок 1) с учётом Rнг и условий измерения.
Рисунок 1
Показания вольтметра 0,92 В
Вариация напряжения в сети питания +10%
Допускаемая погрешность измерения 2,5 %
Сила тока в цепи 2,87 мА
Температура окружающей среды +35 С.
Прежде всего определим Rнг


Эти значения гораздо меньше доп = 2,5 %, поэтому не будем затруднять себя рассчитывать остальные погрешности измерения для этого прибора.
Практически такое же несущественное число получится при анализе характеристик вольтметра Ф203.
В случае использования прибора В7-22 предел измерений установим равным 2 В.

Определим дополнительную погрешность прибора, вызванную вариацией напряжения питания. Анализируя технические характеристики прибора приходим к выводу, что заданная вариация напряжения питания +10В является допускаемым верхним пределом (+22В) нормального значения напряжения в сети питания вольтметра. Таким образом
Исходя из вышесказанного получим:
Определим погрешность из-за несоответствия свойств объекта и прибора по формуле
Учитывая, что при данном диапазоне входное сопротивление составляет 100 МОм получим, что
Исправленное значение показаний вольтметра
Uv = 0,92 + 0,0000029 = 0,9200029
Приближённо погрешность определения поправки равна погрешности определения Rнг. Так как значения I, Rнг, являются маленькими, то погрешность определения поправки является величиной второго порядка малости и ею можно пренебречь.










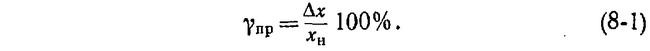
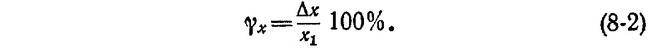
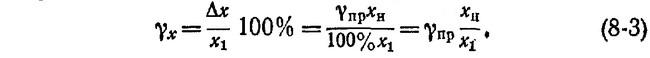
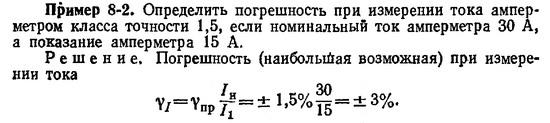
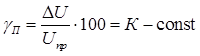

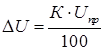

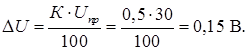
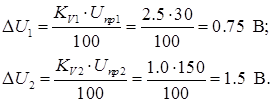
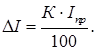
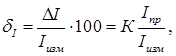
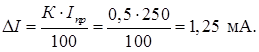
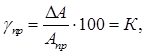
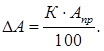
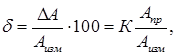
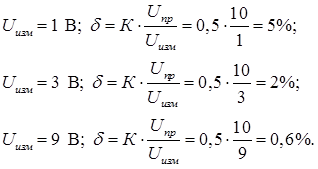
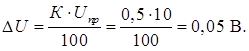
 Погрешность цифровых вольтметров
Погрешность цифровых вольтметров

