Базовый случай рекурсивной функции что такое

Рекурсия. Занимательные задачки

В этой статье речь пойдет о задачах на рекурсию и о том как их решать.

Кратко о рекурсии

Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Один из вариантов увидеть рекурсию – это навести Web-камеру на экран монитора компьютера, естественно, предварительно её включив. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.

В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Простыми словами, рекурсия – определение части функции (метода) через саму себя, то есть это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию).

Задачи

При изучении рекурсии наиболее эффективным для понимания рекурсии является решение задач.

Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде и наоборот. Останется вопрос, надо ли это, и насколько это будет это эффективно.

Для обоснования можно привести такие доводы.

Для начала можно вспомнить определение рекурсии и итерации. Рекурсия — это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ. Итерация — это способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.

После чего можно сделать вывод, что они взаимно заменимы, но не всегда с одинаковыми затратами по ресурсам и скорости. Для обоснования можно привести такой пример: имеется функция, в которой для организации некого алгоритма имеется цикл, выполняющий последовательность действий в зависимости от текущего значения счетчика (может от него и не зависеть). Раз имеется цикл, значит, в теле повторяется последовательность действий — итерации цикла. Можно вынести операции в отдельную подпрограмму и передавать ей значение счетчика, если таковое есть. По завершению выполнения подпрограммы мы проверяем условия выполнения цикла, и если оно верно, переходим к новому вызову подпрограммы, если ложно — завершаем выполнение. Т.к. все содержание цикла мы поместили в подпрограмму, значит, условие на выполнение цикла помещено также в подпрограмму, и получить его можно через возвращающее значение функции, параметры передающееся по ссылке или указателю в подпрограмму, а также глобальные переменные. Далее легко показать, что вызов данной подпрограммы из цикла легко переделать на вызов, или не вызов (возврата значения или просто завершения работы) подпрограммы из нее самой, руководствуясь какими-либо условиями (теми, что раньше были в условии цикла). Теперь, если посмотреть на нашу абстрактную программу, она примерно выглядит как передача значений подпрограмме и их использование, которые изменит подпрограмма по завершению, т.е. мы заменили итеративный цикл на рекурсивный вызов подпрограммы для решения данного алгоритма.

Задача по приведению рекурсии к итеративному подходу симметрична.

Подводя итог, можно выразить такие мысли: для каждого подхода существует свой класс задач, который определяется по конкретным требованиям к конкретной задаче.

Более подробно с этим можно познакомиться тут

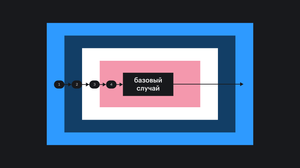
Так же как и у перебора (цикла) у рекурсии должно быть условие остановки — Базовый случай (иначе также как и цикл рекурсия будет работать вечно — infinite). Это условие и является тем случаем к которому рекурсия идет (шаг рекурсии). При каждом шаге вызывается рекурсивная функция до тех пор пока при следующем вызове не сработает базовое условие и произойдет остановка рекурсии(а точнее возврат к последнему вызову функции). Всё решение сводится к решению базового случая. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.

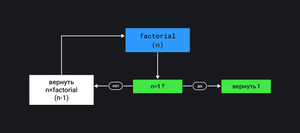
Тут Базовым условием является условие когда n=1. Так как мы знаем что 1!=1 и для вычисления 1! нам ни чего не нужно. Чтобы вычислить 2! мы можем использовать 1!, т.е. 2!=1!*2. Чтобы вычислить 3! нам нужно 2!*3… Чтобы вычислить n! нам нужно (n-1)!*n. Это и является шагом рекурсии. Иными словами, чтобы получить значение факториала от числа n, достаточно умножить на n значение факториала от предыдущего числа.

В сети при обьяснении рекурсии также даются задачи нахождения чисел Фибоначчи и Ханойская башня

Рассмотрим же теперь задачи с различным уровнем сложности.
Попробуйте их решить самостоятельно используя метод описанный выше. При решении попробуйте думать рекурсивно. Какой базовый случай в задаче? Какой Шаг рекурсии или рекурсивное условие?

Поехали! Решения задач предоставлены на языке Java.

A: От 1 до n
Дано натуральное число n. Выведите все числа от 1 до n.

Источник

Задачи по Python с решениями

Свежие записи

Рекурсия. Базовый случай и рекурсивный случай

На этом шаге рассмотрим понятие базового и рекурсивного случая.

Так как рекурсивная функция вызывает сама себя, программисту легко ошибиться и написать функцию так, что возникнет бесконечный цикл. Предположим, вы хотите написать функцию для вывода обратного отсчета:

Ее можно записать в рекурсивном виде:

Введите этот код и выполните его. И тут возникает проблема: эта функция
выполняется бесконечно!

Когда вы пишете рекурсивную функцию, в ней необходимо указать, в какой
момент следует прервать рекурсию. Вот почему каждая рекурсивная
функция состоит из двух частей: базового случая и рекурсивного случая.
В рекурсивном случае функция вызывает сама себя. В базовом случае
функция себя не вызывает (чтобы предотвратить зацикливание).

Добавим базовый случай в функцию countdown:

Теперь функция работает так, как было задумано. Это выглядит примерно
так:

Архив с примером на языке С++ можно взять здесь.

Архив с примером на языке Pascal можно взять здесь.

На следующем шаге продолжим рассматривать рекурсию.

Источник

Как работает рекурсия – объяснение в блок-схемах и видео

Представляю вашему вниманию перевод статьи Beau Carnes How Recursion Works — explained with flowcharts and a video.

«Для того чтобы понять рекурсию, надо сначала понять рекурсию»

Рекурсию порой сложно понять, особенно новичкам в программировании. Если говорить просто, то рекурсия – это функция, которая сама вызывает себя. Но давайте попробую объяснить на примере.

Представьте, что вы пытаетесь открыть дверь в спальню, а она закрыта. Ваш трехлетний сынок появляется из-за угла и говорит, что единственный ключ спрятан в коробке. Вы опаздываете на работу и Вам действительно нужно попасть в комнату и взять вашу рубашку.

Вы открываете коробку только чтобы найти… еще больше коробок. Коробки внутри коробок и вы не знаете, в какой из них Ваш ключ. Вам срочно нужна рубашка, так что вам надо придумать хороший алгоритм и найти ключ.

Есть два основных подхода в создании алгоритма для решения данной проблемы: итеративный и рекурсивный. Вот блок-схемы этих подходов:

Какой подход для Вас проще?

В первом подходе используется цикл while. Т.е. пока стопка коробок полная, хватай следующую коробку и смотри внутрь нее. Ниже немного псевдокода на Javascript, который отражает то, что происходит (Псевдокод написан как код, но больше похожий на человеческий язык).

В другом подходе используется рекурсия. Помните, рекурсия – это когда функция вызывает саму себя. Вот второй вариант в псевдокоде:

Оба подхода выполняют одно и тоже. Основный смысл в использовании рекурсивного подхода в том, что однажды поняв, вы сможете легко его читать. В действительности нет никакого выигрыша в производительности от использования рекурсии. Порой итеративный подход с циклами будет работать быстрее, но простота рекурсии иногда предпочтительнее.

Поскольку рекурсия используется во многих алгоритмах, очень важно понять как она работает. Если рекурсия до сих пор не кажется Вам простой, не беспокойтесь: Я собираюсь пройтись еще по нескольким примерам.

Граничный и рекурсивный случай

То, что Вам необходимо принять во внимание при написании рекурсивной функции – это бесконечный цикл, т.е. когда функция вызывает саму себя… и никогда не может остановиться.
Допустим, Вы хотите написать функцию подсчета. Вы можете написать ее рекурсивно на Javascript, к примеру:

Эта функция будет считать до бесконечности. Так что, если Вы вдруг запустили код с бесконечным циклом, остановите его сочетанием клавиш «Ctrl-C». (Или, работая к примеру в CodePen, это можно сделать, добавив “?turn_off_js=true” в конце URL.)

Рекурсивная функция всегда должна знать, когда ей нужно остановиться. В рекурсивной функции всегда есть два случая: рекурсивный и граничный случаи. Рекурсивный случай – когда функция вызывает саму себя, а граничный – когда функция перестает себя вызывать. Наличие граничного случая и предотвращает зацикливание.

И снова функция подсчета, только уже с граничным случаем:

То, что происходит в этой функции может и не быть абсолютно очевидным. Я поясню, что произойдет, когда вы вызовете функцию и передадите в нее цифру 5.

Сначала мы выведем цифру 5, используя команду Console.Log. Т.к. 5 не меньше или равно 1, то мы перейдем в блок else. Здесь мы снова вызовем функцию и передадим в нее цифру 4 (т.к. 5 – 1 = 4).

Мы выведем цифру 4. И снова i не меньше или равно 1, так что мы переходим в блок else и передаем цифру 3. Это продолжается, пока i не станет равным 1. И когда это случится мы выведем в консоль 1 и i станет меньше или равно 1. Наконец мы зайдем в блок с ключевым словом return и выйдем из функции.

Стек вызовов

Рекурсивные функции используют так называемый «Стек вызовов». Когда программа вызывает функцию, функция отправляется на верх стека вызовов. Это похоже на стопку книг, вы добавляете одну вещь за одни раз. Затем, когда вы готовы снять что-то обратно, вы всегда снимаете верхний элемент.

Я продемонстрирую Вам стек вызовов в действии, используя функцию подсчета факториала. Factorial(5) пишется как 5! и рассчитывается как 5! = 5*4*3*2*1. Вот рекурсивная функция для подсчета факториала числа:

Теперь, давайте посмотрим что же происходит, когда вы вызываете fact(3). Ниже приведена иллюстрация в которой шаг за шагом показано, что происходит в стеке. Самая верхняя коробка в стеке говорит Вам, что вызывать функции fact, на которой вы остановились в данный момент:

Заметили, как каждое обращение к функции fact содержит свою собственную копию x. Это очень важное условие для работы рекурсии. Вы не можете получить доступ к другой копии функции от x.

Нашли уже ключ?

Давайте кратенько вернемся к первоначальному примеру поиска ключа в коробках. Помните, что первым был итеративный подход с использованием циклов? Согласно этому подходу Вы создаете стопку коробок для поиска, поэтому всегда знаете в каких коробках вы еще не искали.

Но в рекурсивном подходе нет стопки. Так как тогда алгоритм понимает в какой коробке следует искать? Ответ: «Стопка коробок» сохраняется в стеке. Формируется стек из наполовину выполненных обращений к функции, каждое из которых содержит свой наполовину выполненный список из коробок для просмотра. Стек следит за стопкой коробок для Вас!

И так, спасибо рекурсии, Вы наконец смогли найти свой ключ и взять рубашку!

Вы также можете посмотреть мое пятиминутное видео про рекурсию. Оно должно усилить понимание, приведенных здесь концепций.

Заключение от автора

Надеюсь, что статья внесла немного больше ясности в Ваше понимание рекурсии в программировании. Основой для статьи послужил урок в моем новом видео курсе от Manning Publications под названием «Algorithms in Motion». И курс и статься написаны по замечательной книге «Grokking Algorithms», автором которой является Adit Bhargava, кем и были нарисованы все эти замечательные иллюстрации.

И наконец, чтобы действительно закрепить свои знания о рекурсии, Вы должны прочитать эту статью, как минимум, еще раз.

От себя хочу добавить, что с интересом наблюдаю за статьями и видеоуроками Beau Carnes, и надеюсь что Вам тоже понравилась статья и в особенности эти действительно замечательные иллюстрации из книги A. Bhargav «Grokking Algorithms».

Источник

Рекурсия

Время чтения: больше 15 мин

Обновлено 27 октября 2021

Кратко

Рекурсия — это что-то, что описывает само себя.

Представить рекурсию проще всего на примере зеркального коридора — когда напротив друг друга стоят два зеркала. Если посмотреть в одно, то в нём будет отражение второго, во втором — отражение первого и так далее.

В «Начале» Нолана есть момент с зеркальным коридором, когда в отражении зеркала видно отражение зеркала, в котором видно отражение зеркала, в котором видно.

Второй пример, чуть более академически правильный — это фрактал. Тот же треугольник Серпинского — это пример рекурсии, потому что часть фигуры — это одновременно вся фигура.

Треугольник состоит из 3 точно таких же треугольников.

Рекурсия в программировании

В программировании под рекурсией чаще всего понимают функцию, которая вызывает саму себя.

При решении некоторых задач мы можем обнаружить, что решение можно разбить на несколько простых действий и более простой вариант той же задачи.

Например, при возведении числа в степень мы берём число, умножаем его на себя несколько раз. Эту операцию можно представить в виде:

Но это же можно представить в виде нескольких последовательных умножений на 2:

При таком представлении всё возведение в степень — это лишь умножение предыдущего результата на 2:

Именно такие задачи называются рекурсивными — когда часть условия ссылается на всю задачу в целом (или похожую на неё).

У рекурсии 2 составляющие: повторяющиеся операции и базовый случай.

Повторяющиеся операции

В примере с возведением в степень повторяющиеся операции — это умножение.

Такие операции могут быть сложными и включать в себя несколько подзадач. Такое, например, часто встречается в математике.

Базовый случай

Вторая важная часть рекурсии — это базовый случай.

Базовый случай — это условие, при выполнении которого рекурсия заканчивается и функция больше не вызывает саму себя.

Например, при возведении в степень базовый случай наступает, когда значение степени становится равно искомому.

Как только выполнение доходит до базового случая, оно останавливается.

Без базового случая любая рекурсивная функция уйдёт в бесконечное выполнение, потому что будет вызывать себя без конца.

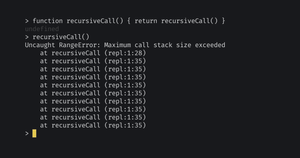
В JS это приводит к переполнению стека вызовов, и функция останавливается с ошибкой.

Если выполнить функцию без базового случая, которая лишь вызывает себя, получим ошибку.

Цикл и рекурсия

Из-за повторяющихся операций рекурсия схожа с циклом. Их часто считают взаимозаменяемыми, но это всё же не совсем так.

Рекурсия проигрывает циклу в следующем:

Цикл же проигрывает рекурсии в таких вещах:

Поэтому на вопрос «Что использовать: рекурсию или цикл?» ответом будет «Зависит от задачи», серебряной пули здесь нет :–)

Давайте решим одну и ту же задачу с использованием цикла и рекурсии, чтобы увидеть разницу в подходах. Будем писать функцию для нахождения факториала.

Факториал числа — это произведение всех чисел от единицы до этого числа. Например, факториал 5 — это произведение (1 × 2 × 3 × 4 × 5) = 120.

Факториал с помощью цикла

Сперва решим задачу нахождения факториала с помощью цикла.

В этой функции мы используем цикл, чтобы умножить каждое число на результат предыдущего умножения. То же самое мы можем сделать и рекурсивно.

Факториал с помощью рекурсии

Для расчёта факториала рекурсивно мы создадим функцию, в которой в первую очередь опишем базовый случай, а уже потом — повторяющиеся действия.

Хорошим правилом при работе с рекурсией считается первым делом описывать базовый случай (как ранний выход, early return) и только потом — всё остальное. Это позволяет сделать работу с рекурсией безопаснее.

В виде блок-схемы мы можем представить алгоритм факториала как условие и под-вызов той же функции.

Кроме того, что функция стала заметно короче, она теперь выражает непосредственно математическую суть факториала.

Разберём по шагам, что происходит с переменной n и результатом функции factorial после каждого вызова:

Минусы такой реализации:

Рекурсивные структуры данных

Раньше мы упомянули, что в программировании чаще всего под рекурсией понимают функцию, которая вызывает сама себя. Но кроме рекурсивных функций ещё есть рекурсивные структуры данных.

Структура данных — это контейнер, который хранит данные в определённом формате. Этот контейнер решает, каким образом внешний мир может эти данные считать или изменить.

Структуры данных, части которых включают в себя такие же структуры, называются (вы угадали) рекурсивными. Работать с такими структурами в цикле не очень удобно. Чтобы понять почему, рассмотрим пример одной из рекурсивных структур данных — дерева.

Деревья

Дерево — это структура, в которой у каждого узла может быть несколько дочерних подузлов — «детей».

Мы уже встречались с деревьями в статье «Как браузер рисует страницы». Мы рассматривали DOM, CSSOM и Render Tree. Вспомним, как выглядит DOM-дерево.

Работать с деревьями с помощью циклов (итеративно) неудобно. Представьте, что мы хотим получить названия всех элементов на странице. Да, мы можем пройтись циклом по 1-му уровню или 2-му, но дальше нужно думать, как определять, где мы были, где ещё нет и куда идти дальше.

С рекурсией обход дерева становится немного проще.

Рекурсивный обход

В случае с рекурсией мы можем придумать например такой алгоритм для обхода дерева:

Когда использовать рекурсию

Сама по себе рекурсия — это всего лишь инструмент. Нет чётких правил, когда её надо использовать, а когда — нет. Есть лишь некоторые рекомендации.

Источник

Простыми словами о рекурсии

Dec 19, 2020 · 4 min read

В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.

Рекурсию также можно сравнить с матрёшкой. Первая кукла самая большая, за ней идёт точно такая же кукла, но поменьше. Суть матрёшки состоит в том, что вы можете открывать её и доставать из неё точно такую же куклу, только немного меньше. Такой продолжительный процесс длится до тех пор, пока вы не дойдёте до последней куклы, которая и прервёт цикл. Так выглядит визуальная репрезентация рекурсии.

Не приведёт ли рекурсивная функция к бесконечному циклу?

Вот пример кода того, как можно реализовать функцию обратного отсчёта с использованием рекурсии:

Как прервать рекурсию:

Проще говоря, рекурсия делает то же, что и код ниже:

Плюсы и минусы рекурсивных функций

Чтобы правильно описать плюсы и минусы, давайте взглянем на производительность рекурсии.

Плюсы:

Под этим подразумевается, что рекурсии, в сравнении с циклами, тратят меньше времени до завершения функции. Чем меньше строк кода у нас будет, тем быстрее функция будет обрабатывать вызовы внутри себя. Особенно хорошо это проявляется при буферизации данных, что позволяет оптимизировать и ускорить код.

В программировании мемоизация — это метод сохранения результатов выполнения функций для предотвращения повторных вычислений. Это один из способов оптимизации, применяемый для увеличения скорости выполнения программ. — Википедия

И всё же стоит отметить, что рекурсия не всегда выигрывает по скорости по сравнению с циклами.

Многие согласятся, что эта причина очень важна. Рекурсия проста в отладке из-за того, что она не содержит сложных и длинных конструкций.

Минусы:

Рекурсивные функции занимают значительный объём памяти во время своего выполнения. Это означает, что при каждом вызове функции в стек будет добавляться новый элемент, который будет занимать место до тех пор, пока функция не завершит работу, найдя ответ, либо пока не дойдёт до выполнения базового условия функции.

Что такое «стек»?

Стек — это такая структура данных, которая работает по принципу «Last In, First Out» (последним пришёл — первым ушёл). Таким образом, элемент «проталкивается» в стек и добавляется в его конец, а затем «выталкивается» из стека при удалении.

Стоит ли использовать рекурсии вместо обычных циклов?

Оба этих метода одинаково эффективны для решения задач, однако выбор одного из них зависит от типа проблемы, поставленной перед вами.

Рекурсии эффективны тогда, когда вы работаете с данными, которые слишком сложны, чтобы пройтись по ним с помощью обычных циклов. Стоит также не забывать о ценности памяти и уменьшении времени, идущем вкупе с рекурсивной функцией, в которой накопилось слишком много элементов.

Циклы так же эффективны в плане скорости и оптимизации, они занимают меньше памяти в стеке и их легче понять, потому что в теле цикла содержится больше информации о том, что происходит внутри.

Источник